NP-Vollständigkeit
From Alda
Die Problemklassen P und NP
- fundamentale Unterscheidung:
- Komplexität O(<math>n^p</math>), p < ∞ (n = Problemgröße), ⇒ ist eventuell effizient
- exponentielle Komplexität O(<math>2^n</math>), O(<math>2^{\sqrt{n}}</math>), ⇒ prinzipiell nicht effizient
- Vereinfachung:
- betrachte nur Entscheidungsprobleme, d.h. Algorithmen, die True/False liefern
- z.B. BP: „Gibt es einen Pfad der Länge ≤ L?“
- Klasse P: alle Algorithmen, die in polynomieller Zeit eine Lösung finden,
- Klasse NP: Alle Algorithmen, wo man eine gegebene Lösung in polynomieller Zeit überprüfen kann
- Ungelöstes Problem: Sind alle Probleme in NP auch in P? („P = NP?“)
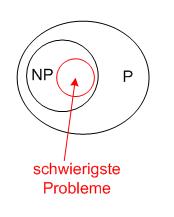
- Welches sind die schwierigsten Probleme in NP?
- => die, sodass man alle anderen NP-Probleme in diese umwandeln kann: „NP vollständig“, „NP complete“
- umwandeln:
- Problem wird auf ein anderes reduziert
- Reduktion darf nur polynomielle Zeit erfordern (d.h. alle Zwischenschritte müssen polynomiell sein)
3-SAT ist NP vollständig
Skizze des Beweises:
- Unsere Algorithmen können auf einer Turingmaschine ausgeführt werden (äquivalent zur Turingmaschine: λ-Kalkül, while-Programm usw.)
- Die Turingmaschine und ein gegebenes (festes) Programm können als logische Schaltung (Schaltnetz) implementiert werden, „Algorithmus in Hardware gegossen“
- Jedes Schaltnetzwerk kann als logische Formel geschrieben werden, z.B.:
- 4. Jede logische Formel kann in 3-CNF umgewandelt werden
- => Jedes algorithmische Entscheidungsproblem kann als 3-SAT-Problem geschrieben werden.