Greedy-Algorithmen und Dynamische Programmierung

Einführung

Viele Probleme sind durch einen Entscheidungsbaum systematisch lösbar.

Dabei wird die zu suchende Lösung auf den optimalen Weg durch den Entscheidungsbaum reduziert.

Beispiel

Erklärung des Algorithmus ist zu finden in Graphen und Graphenalgorithmen

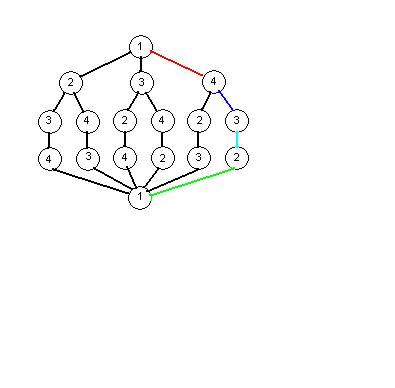
Traveling Salesman Problem mit 4 Knoten

Dabei entsteht folgender Entscheidungsbaum:

Vorteil des Entscheidungsbaums: Lösungsmöglichkeiten werden nicht übersehen

Nachteil: Eventuell muss der gesamte Baum durchsucht werden (exponentielle Komplexität)

Um diesen Nachteil auszugleichen gibt es verschiedene Verfahren:

• Divide & Conquer (Problem auf triviale Teilprobleme zurückführen, welche jeweils einfach zu lösen sind)
• Greedy Algorithmen
• Dynamische Programmierung

Greedy Algorithmen

Greedy (dt. "Gierig") Algorithmen entscheiden an jedem Knoten lokal über die beste Fortsetzung der Suche,

d.h. es wird jeweils die beste Entscheidung im Kleinen getroffen - ohne Rücksicht auf Konsequenzen für den gesamten Suchverlauf.

Beispiele

Anwendung beim Traveling Salesman Problem

Erklärung des Algorithmus ist zu finden in Graphen und Graphenalgorithmen

Reise immer zum nächstgelegenen, noch nicht besuchten Knoten:

In diesem Beispiel wurde eine optimale Lösung gefunden. Dies muss im Allgemeinen aber nicht immer der Fall sein!

Anwendung beim Algorithmus von Kruskal für Minium Spanning Tree

Erklärung des Algorithmus ist zu finden in Graphen und Graphenalgorithmen

• Sortiere die Kanten nach Gewicht
• Wähle stets die Kante mit niedrigstem Gewicht (d.h. im Allgemeinen die nächsgelegene), die keinen Zyklus verursacht

Hierbei wird der Minimum Spanning Tree stets gefunden.

Dynamische Programmierung

(Programmierung hat hier eine Bedeutung die sich nicht auf Programmiersprachen bezieht)

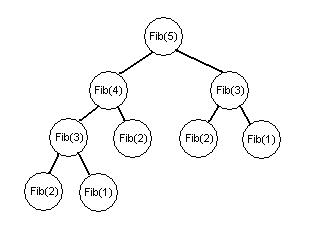
Oft ist dasselbe Teilproblem in mehreren Pfaden vorhanden.

Beispiel

Im Beispiel mit Fibonacci-Zahlen wird Fib(2) gleich dreimal benötigt.

Zur Erinnerung: Die Fibonacci-Folge <math>(f_0, f_1,\ldots)</math> ist durch das rekursive Bildungsgesetz

<math> f_n = f_{n-1} + f_{n-2}\ </math>   für <math>n\geq 2</math>

mit den Anfangswerten

<math>f_0=0\ </math>   und   <math>f_1=1\ </math>

definiert.

Konzept der Dynamische Programmierung

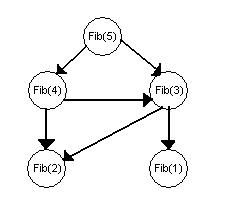
Jedes Teilproblem soll nur einmal gelöst werden, d.h. einige Knoten werden mehrmals genutzt:

Wie im Beispiel erkennbar, hat sich die Zahl der Knoten drastisch reduziert (von 9 auf 5).

Allerdings müssen die Graphen jetzt gerichtet sein.

Wenn der neue Graph azyklisch ist, kann man die Teilprobleme so anordnen, dass jedes

• nur einmal gelöst wird
• nur von bereits gelösten Teilproblemen abhängt

Wenn der Graph nicht azyklisch ist (weil z.B. Teilproblem A die Lösung von Teilproblem B erfordert und umgekehrt),

ist die Dynamische Programmierung auf dieses Problem nicht anwendbar.

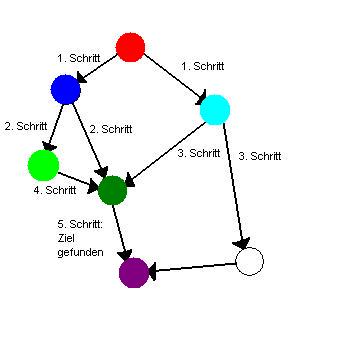
Dynamisch programmierter Dijkstra Alrogithmus

Erklärung des Algorithmus ist zu finden in Graphen und Graphenalgorithmen

Löse Teilprobleme entsprechend ihrer Priorität, d.h. Priorität definiert die Ordnung

Problem: Der Suchbaum ist bei diesem Algorithmus ungerichtet

Lösung: Die Richtung der Kanten wird festgelegt, wenn man die Nachbarn eines Knotens in die Queue eingefügt

Wenn man den Abstand vom Start bestimmt (Teilproblem), ist der Abstand von allen näher gelegenen bereits bekannt.

Greedy oder Dynamische Programmierung?

Für viele Probleme gibt es unterschiedliche Entscheidungsräume und/oder unterschiedliche Entscheidungskriterien.

Ein und dasselbe Problem kann also mit einer der Darstellungen (Greedy, Dynamische Programmierung, weitere...) effizient lösbar sein, mit anderen eventuell nicht.

Das finden einer geeigneten Darstellung ist also eine zentrale Herausforderung.

Anwendungsbeispiel: Interval Scheduling

gegeben:

Mehrere Aufgaben mit unterschiedlichen Anfangszeiten <math>s_i</math> und Endzeiten <math>f_i</math>.

Es kann immer nur eine Aufgabe gleichzeitig bearbeitet werden: zwei Aktivitäten sind kompatibel, wenn deren Zeiten sich nicht überlappen.

<math>a_k\,\text{komp}\, a_j \Leftrightarrow s_k\geq f_j\, \or \, s_j\geq f_k</math>

gesucht:

Arbeitsplan um möglichst viele Aufgaben nacheinander abzuarbeiten.

Dabei haben alle Aufgaben dieselbe Priorität, obwohl die Dauer oft unterschiedlich ist.

Mögliche Lösungsansätze für einen Greedy Algorithmus

1. Wähle (unter kompatiblen) die Aktivität, die als erste startet
2. Wähle (unter kompatiblen) die Aktivität, die als erste endet (oder: die als letzte startet)
3. Wähle (unter kompatiblen) die Aktivität, die am kürzesten dauert
4. Wähle (unter kompatiblen) die Aktivität, die die wenigsten Inkompatibilitäten (überlappungen mit anderen Aktivitäten) hat

Ungünstige Ansätze:

In den folgenden Beispielen werden die Aktivitäten mit | als Anfangs- bzw Endzeit markiert, --- steht für den Verlauf einer Aktivität.

Weiter rechts bedeutet später in der Zeit.

Gegenbeispiel zu 1.

    <math>L_1=</math>  |--| |--| |--| |--|
    <math>L_2=</math>|---------------------|
    <math>|L_1|</math>=4 <math>|L_2|</math>=1

Der Ansatz würde Lösung 2 wählen, da die lange Aktivität am frühesten beginnt. Es wird dann nur 1 statt der optimalen 4 abgearbeitet.

Gegenbeispiel zu 3.

    <math>L_1=</math>|---------| |---------|
    <math>L_2=</math>        |----|
    <math>|L_1|</math>=2 <math>|L_2|</math>=1

Der Ansatz würde Lösung 2 wählen, da die mittlere Aktivität am kürzesten dauert. Es wird dann nur 1 statt der optimalen 2 abgearbeitet.

Gegenbeispiel zu 4. (Anzahl der Inkompatibilitäten stehen jeweils in der Mitte der Aktivität)

    |-3-| |-4-| |-4-| |-3-|
       |-4-| |-2-| |-4-|
       |-4-|       |-4-|
       |-4-|       |-4-|

Der Ansatz würde erst die mit 2, dann die beiden mit 3 Inkompatibilitäten wählen. Es werden dann nur 3 statt der optimalen 4 (obere Zeile) abgearbeitet.

Es verbleibt der 2. Ansatz, dessen Optimalität noch zu beweisen ist...

Greedy Stays Ahead

Idee der Beweismethode

Es genügt zu zeigen:

die Greedy-Lösung ist nicht schlechter als die optimale Lösung

Beweis der Optimalität des 2. Ansatzes mit Greedy Stays Ahead

Ansatz

Wähle (unter kompatiblen) die Aktivität, die als erste endet (oder: die als letzte startet)

Die Wahl dieses Ansatzes sei <math>U={i_1,...,i_k}</math>.

Eine (unbekannte) optimale Lösung sei <math>O={j_1,...,j_m}</math>.

Ziel

Die Lösung des Ansatzes soll genausoviele Aktivitäten schaffen wie die optimale Lösung (d.h. k=m)

Voraussetzungen

• Sortiere <math>i_1,...,i_k</math> nach aufsteigender Endzeit <math>Fi</math>
• Sortiere <math>j_1,...,j_m</math> nach aufsteigender Endzeit <math>Fj</math>

(Da die Aktivitäten kompatibel sind, werden die Anfangszeiten automatisch auch sortiert)

Schritt 1

Für die Indizes <math>p\leq r</math> (inbesondere <math>p=r</math>) gilt: <math>f(i_p)\leq f(j_r)</math>

Beweis durch vollständige Induktion

Induktions-Anfang:

<math>f(i_1)\leq f(j_1)</math>, da <math>i_1</math> die erste Aktivität ist, die überhaupt endet

Induktions-Voraussetzung:

<math>f(i_{r-1})\leq f(j_{r-1})</math>

Induktions-Schritt:

Wegen Kompatibilität gilt:

<math>f(j_{r-1})\leq s(j_r)</math>

=> <math>f(i_{r-1})\leq s(i_r)</math>

=> Die Greedy Strategie kann Aktivität <math>j_r</math> wählen, denn sie ist kompatibel mit <math>i_{r-1}</math>

• Wenn die Greedy Strategie tatsächlich <math>j_r</math> wählt, folgt daraus:

<math>f(i_r)=f(j_r)</math>

• Wenn nicht, kann nur gelten:

<math>f(i_r)\leq f(j_r)</math>

Schritt 2

Zu zeigen: <math>k=m</math>

Beweis durch Widerspruchsannahme

• Falls <math>m<k</math>, wäre die Lösung der Strategie besser als die optimale.
• Angenommen <math>m>k</math>, dann enthält <math>O</math> eine Aktivität <math>j_{k+1}</math>.

Nach Schritt 1 gilt:

<math>f(i_k)\leq f(j_k)\leq f(j_{k+1})</math>

Wegen Kompatibilität gilt aber:

<math>s(j_{k+1})\geq f(j_k)\geq f(i_k)</math>

-> Die Greedy Strategie hätte also noch die Aktivität <math>j_{k+1}</math> wählen können.

-> Widerspruch zur Annahme, dass die Greedy Strategie durchgelaufen ist, bis keine Aktivität mehr hinzugefügt werden kann

-> m>k ist falsch

-> m=k ist richtig

Beispiel zur Dynamischen Programmierung: Wighted Intervall Scheduling

Die Problemstellung ähnelt dem des normalen Intervall Scheduling, hier haben die Aktivitäten aber Gewichte <math>w_i</math>

(z.B. Bringt eine längere Aufgabe in einem Übunsgzettel in der Regel auch mehr Punkte, d.h. sie hat eine hohe Gewichtung)

Ziel

Wähle die Aktivitäten so, dass der Gewinn (Summe der Gewichtungen der bearbeiteten Aktivitäten) maximal wird.

Ansatz

• Sortiere Aktivitäten nach ihrer Endzeit.
• Definiere eine Funktion <math>p(i)</math>, welche für die Aktivität steht, die vor <math>a_i</math> endet, mit <math>a_i</math> kompatibel ist, unter allen Aktivitäten mit diesen Eigenschaften die letzte (d.h. mit der spätesten Endzeit) ist.

In folgendem Beispiel wird die Aktivität <math>a_i</math> mit der Symbolik |-!-| betrachtet um deren p-Funktion zu evaluieren.

Für die p-Funktion kommen lediglich die Funktionen mit der Symbolik |===| und |====| in Frage, die untere der beiden ist die gesuchte Aktivität.

   |====|        |-!-| |--|
       |===| |-----|         |----|

Trivial ist, dass <math>a_n</math> entweder zur Lösung gehört, oder nicht:

Dadurch ergibt sich folgende Funktion:

<math>OPT(n)=\begin{cases}

\ \;\, \{a_n\}\cup OPT(p(n))\\ \ \;\, OPT(a_{n-1}) \end{cases} </math>

Um den höchstmöglichen Gewinn zu erzielen, wird <math>\{a_n\}\cup OPT(p(n))</math> verwendet falls gilt:

<math>w_n + Gewinn(OPT(p(n))\leq Gewinn(OPT(n-1))</math>

Ansonsten wird <math>OPT(a_{n-1})</math> angewandt.