Graphen und Graphenalgorithmen
Einführung zu Graphen
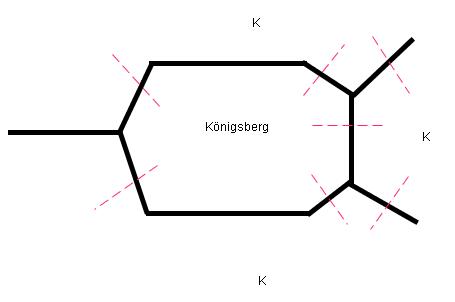
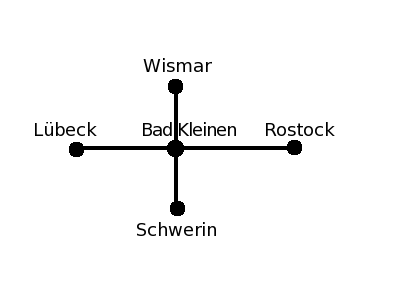
Motivation -- Königsberger Brückenproblem
Leonhard Euler [1] erfand den Graphen-Formalismus 1736, um eine scheinbar banale Frage zu beantworten: Ist es möglich, in Königsberg (siehe Stadtplan von 1809 und die schematische Darstellung) einen Spaziergang zu unternehmen, bei dem jede der 7 Brücken genau einmal überquert wird?
Ein Graph abstrahiert von der Geometrie des Problems und repräsentiert nur die Topologie. Jeder Stadtteil von Königsberg ist ein Knoten des Graphen, jede Brücke eine Kante. Der zum Brückenproblem gehörende Graph sieht also so aus:
O
/| \
\| \
O---O
/| /
\| /
O
Der gesuchte Spaziergang würde existieren, wenn es maximal 2 Knoten gäbe, an denen sich eine ungerade Zahl von Kanten trifft. Die Frage muss für Königsberg also verneint werden, denn hier gibt es vier solche Knoten.
Inzwischen haben Graphen ein riesige Zahl weiterer Anwendungen gefunden. Einige Beispiele:
- Landkarten:
- Knoten: Länder
- Kanten: gemeinsame Grenzen
- Logische Schaltkreise:
- Knoten: Gatter
- Kanten: Verbindungen
- Chemie (Summenformeln):
- Knoten: chemische Elemente
- Kanten: Bindungen
- Soziologie (StudiVZ)
- Soziogramm
- Knoten: Personen
- Kanten: Freund von ...
- Soziogramm
Definitionen
- Ungerichteter Graph
- Ein ungerichteter Graph G = ( V, E ) besteht aus
- einer endliche Menge V von Knoten (vertices)
- einer endlichen Menge von Kanten (edges)
- Die Paare (u,v) und (v,u) gelten dabei als nur eine Kante (somit gilt die Symmetriebeziehung: (u,v) ∈ E => (v,u) ∈ E ). Die Anzahl der Kanten, die sich an einem Knoten treffen, wird als Grad (engl. degree) dieses Knotens bezeichnet:
- degree(v) = |{v' ∈ V | (v,v') ∈ E}|
- (Die Syntax |{...}| bezeichnet dabei die Mächtigkeit der angegebenen Menge, also die Anzahl der Elemente in der Menge.)
Der Graph des Königsberger Brückenproblems ist ungerichtet. Bezeichnet man die Knoten entsprechend des folgenden Bildes
c /| \ \| \ b---d /| / \| / a
gilt für die Knotengrade: degree(a) == degree(c) == degree(d) == 3 und degree(b) == 5. Genauer muss man bei diesem Graphen von einem Multigraphen sprechen, weil es zwischen einigen Knotenpaaren (nämlich (a, b) sowie (b, c)) mehrere Kanten ("Mehrfachkanten") gibt. Wir werden in dieser Vorlesung nicht näher auf Multigraphen eingehen.
- Gerichteter Graph
- Ein Graph heißt gerichtet, wenn die Kanten (u,v) und (v,u) unterschieden werden. Die Kante (u,v) ∈ E wird nun als Kante von u nach v (aber nicht umgekehrt) interpretiert. Entsprechend unterscheidet man jetzt den eingehenden und den ausgehenden Grad jedes Knotens:
- out_degree(v) = |{v' ∈ V | (v,v') ∈ E}|
- in_degree(v) = |{v' ∈ V| (v',v) ∈ E}|
- out_degree(v) = |{v' ∈ V | (v,v') ∈ E}|
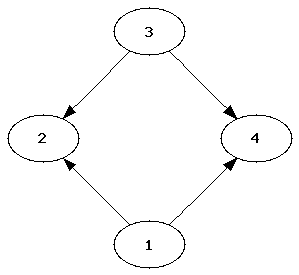
Das folgende Bild zeigt einen gerichteten Graphen. Hier gilt out_degree(1) == out_degree(3) == in_degree(2) == in_degree(4) == 2 und in_degree(1) == in_degree(3) == out_degree(2) == out_degree(4) == 0:
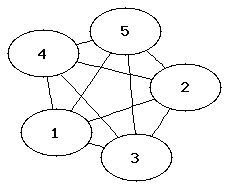
- Vollständiger Graph
- Ein vollständiger Graph ist ein ungerichteter Graph, bei dem jeder Knoten mit allen anderen Knoten verbunden ist.
- Ein vollständiger Graph mit |V| Knoten hat Kanten.
Die folgenden Abbildungen zeigen die vollständigen Graphen mit einem bis fünf Knoten (auch als K1 bis K5 bezeichnet).
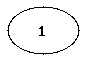 |
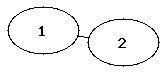 |
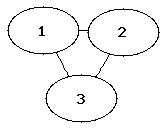 |
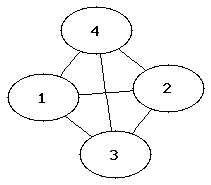 |
 |
Rätsel
Auf einer Party sind Leute. Alle stoßen miteinander an. Es hat 78 mal "Pling" gemacht.
Wieviele Leute waren da? Antwort: Jede Person ist ein Knoten des Graphen, jedes Antoßen eine Kante.
Da alle miteinander angestoßen haben, handelt es sich um einen vollständigen Graphen. Mit
|V|(|V|-1)/2 = 78 folgt, dass es 13 Personen waren.
- Gewichteter Graph
- Ein Graph heißt gewichtet, wenn jeder Kante eine reelle Zahl zugeordnet ist. Bei vielen Anwendungen beschränkt man sich auch auf nichtnegative reelle Gewichte. In einem gerichteten Graphen können die Gewichte der Kanten (u,v) und (v,u) unterschiedlich sein.
Die Gewichte kodieren Eigenschaften der Kanten, die für die jeweilige Anwendung interessant sind. Bei der Berechnung des maximalen Flusses in einem Netzwerk sind die Gewichte z.B. die Durchflusskapazitäten jeder Kante, bei der Suche nach kürzesten Weges kodieren Sie den Abstand zwischen den Endknoten der Kante, bei Währungsnetzwerken (jeder Knoten ist eine Währung) geben sie die Wechselkurse an, usw..
- Teilgraphen
- Ein Graph G' = (V',E') ist ein Teilgraph eines Graphen G, wenn gilt:
- V' ⊆ V
- E' ⊂ E
- Er heißt (auf)spannender Teilgraph, wenn gilt:
- V' = V
- Er heißt induzierter Teilgraph, wenn gilt:
- e = (u,v) ∈ E' ⊂ E ⇔ u ∈ V' und v ∈ V'
- Den von V' induzierten Teilgraphen erhält man also, indem man aus G alle Knoten löscht, die nicht in V' sind, sowie alle Kanten (und nur diese Kanten), die einen der gelöschten Knoten als Endknoten haben.
- Wege, Pfade, Zyklen, Kreise, Erreichbarkeit
- Sei G = (V,E) ein Graph (ungerichtet oder gerichteter) Graph. Dann gilt folgende rekursive Definition:
- Für v ∈ V ist (v) ein Weg der Länge 0 in G
- Falls ein Weg ist, und eine Kante existiert, dann ist auch ein Weg, und er hat die Länge n.
- Ein Weg ist also eine nichtleere Folge von Knoten, so dass aufeinander folgende Knoten stets durch eine Kante verbunden sind. Die Länge des Weges entspricht der Anzahl der Kanten im Weg (= Anzahl der Knoten - 1).
- Ein Pfad ist ein Weg, bei dem alle Knoten vi verschieden sind.
- Ein Zyklus ist ein Weg, der zum Ausgangspunkt zurückkehrt, wenn also v0 = vn gilt.
- Ein Kreis ist ein Zyklus ohne Überkreuzungen. Das heisst, es gilt v0 = vn und ist ein Pfad.
- Ein Knoten w ∈ V ist von einem anderen Knoten v ∈ V aus erreichbar genau dann, wenn ein Weg (v, ..., w) existiert. Wir schreiben dann .
In einem ungerichteten Graph ist die Erreichbarkeits-Relation stets symmetrisch, das heisst aus folgt . In einem gerichteten Graphen ist dies im allgemeinen nicht der Fall.
Bestimmte Wege haben spezielle Namen
- Eulerweg
- Ein Eulerweg ist ein Weg, der alle Kanten genau einmal enthält.
Die eingangs erwähnte Frage des Königsberger Brückenproblems ist equivalent zu der Frage, ob der dazugehörige Graph einen Eulerweg besitzt (daher der Name). Ein anderes bekanntes Beispiel ist das "Haus vom Nikolaus": Wenn man diesen Graphen in üblicher Weise in einem Zug zeichnet, erhält man gerade den Eulerweg.
O / \ O----O | \/ | | /\ | "Das Haus vom Nikolaus": Alle Kanten werden nur einmal passiert O----O
- Hamiltonweg
- Ein Hamiltonweg ist ein Weg, der alle Knoten genau einmal enthält. Das "Haus vom Nikolaus" besitzt auch einen Hamiltonweg:
O
/
O----O
/
/ Alle Knoten werden nur einmal passiert
O----O
- Hamiltonkreis
- Ein Hamiltonkreis ist ein Kreis, der alle Knoten genau einmal enthält. Auch ein solches Gebilde ist im Haus von Nilolaus enthalten:
O / \ O O | | v0 = vn | | vi != vj Für Alle i,j i !=j; i,j >0; i,j < n O----O
Die folgende Skizze zeigt hingegen einen Zyklus: Der Knoten rechts unten sowie die untere Kante sind zweimal enthalten (die Kante einmal von links nach rechts und einmal von rechts nach links):
O
/ \
O O
\ |
\ | Zyklus
O====O
- Zusammenhang, Zusammenhangskomponenten
- Ein ungerichteter Graph G heißt zusammenhängend, wenn für alle v,w ∈ V gilt:
- Ein gerichteter Graph G ist zusammenhängend, wenn für alle v,w ∈ V gilt:
- oder .
- Er ist stark zusammenhängend, wenn für alle v,w ∈ V gilt:
- und .
- Entsprechende Definitionen gelten für Teilgraphen G'. Ein Teilgraph G' heisst Zusammenhangskomponente von G, wenn er ein maximaler zusammenhängender Teilgraph ist, d.h. wenn G' zusammenhängend ist, und man keine Knoten und Kanten aus G mehr zu G' hinzufügen kann, so dass G' immer noch zusammenhängend bleibt. Entsprechend definiert man starke Zusammenhangskomponenten in einem gerichteten Graphen.
- Planarer Graph, ebener Graph
- Ein Graph heißt planar, wenn er so in einer Ebene gezeichnet werden kann, dass sich die Kanten nicht schneiden (außer an den Knoten). Ein Graph heißt eben, wenn er tatsächlich so gezeichnet ist, dass sich die Kanten nicht schneiden. Die Einbettung in die Ebene ist im allgemeinen nicht eindeutig.
Beispiele:
Der folgende Graph ist planar und eben:
O
/|\
/ O \
/ / \ \
O O
Das "Haus vom Nikolaus" ist ebenfalls planar, wird aber üblicherweise nicht als ebener Graph gezeichnet, weil sich die Diagonalen auf der Wand überkreuzen:
O / \ O----O | \/ | | /\ | O----O
Eine ebene Einbettung dieses Graphen wird erreicht, wenn man eine der Diagonalen ausserhalb des Hauses zeichnet. Der Graph (also die Menge der Knoten und Kanten) ändert sich dadurch nicht.
O
/ \
--O----O
/ | / |
| | / |
| O----O Das "Haus vom Nikolaus" als ebener Graph gezeichnet.
\ /
-----
Eine alternative Einbettung erhalten wir, wenn wir die andere Diagonale außerhalb des Hauses zeichnen:
O
/ \
O----O--|
| \ | |
| \ | |
O----O | Alternative Einbettung des "Haus vom Nikolaus".
| |
|-------|
Jede Einbettung eines planaren Graphen (also jeder ebene Graph) definiert eine eindeutige Menge von Regionen:
|----O @ | /@ \ | O----O | |@ / | | | / @| | O----O @ entspricht jeweils einer Region. Auch ausserhalb der Figur ist eine Region (die sogenannte unendliche Region). |@ | |-------|
Der vollständige Graph K5 ist kein planarer Graph, da sich zwangsweise Kanten schneiden, wenn man diesen Graphen in der Ebene zeichnet.
- Dualer Graph
- Jeder ebene Graph G = (V, E) hat einen dualen Graphen D = (VD, ED), dessen Knoten und Kanten wie folgt definiert sind:
- VD enthält einen Knoten für jede Region des Graphen G
- Für jede Kante e ∈ E gibt es eine duale Kante eD ∈ ED, die die an e angrenzenden Regionen (genauer: die entsprechenden Knoten in D) verbindet.
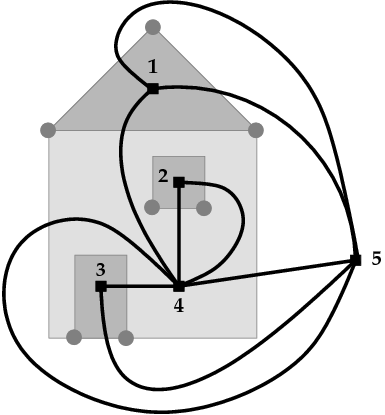
Die folgende Abbildung zeigt einen Graphen (grau) und seinen dualen Graphen (schwarz). Die Knoten des dualen Graphen sind mit Zahlen gekennzeichnet und entsprechen den Regionen des Originalgraphen. Jeder (grauen) Kante des Originalgraphen entspricht eine (schwarze) Kante des dualen Graphen.
Für duale Graphen gilt: Wenn der Originalgraph zusammenhängend ist, enthält jede Region des dualen Graphen genau einen Knoten des Originalgraphen. Deshalb ist der duale Graph des dualen Graphen wieder der Originalgraph. Bei nicht-zusammenhängenden Graphen gilt dies nicht (vgl. das Fenster bei obigem Bild). In diesem Fall hat der duale Graph mehrere mögliche Einbettungen in die Ebene (man kann z.B. die rechte Kante zwischen Knoten 2 und 4 auch links vom Fenster einzeichnen), und man erhält nicht notwendigerweise den Originalgraphen, wenn man den dualen Graphen des dualen berechnet.
- Baum
- Ein Baum ist ein zusammenhängender, kreisfreier Graph.
Beispiel: Binärer Suchbaum
- Spannbaum
- Ein Spannbaum eines zusammenhängenden Graphen G ist ein zusammenhängender, kreisfreier Teilgraph von G, der alle Knoten von G enthält
Beispiel: Spannbaum für das "Haus des Nikolaus"
O / O O | / | / O----O
Der Spannbaum eines Graphen mit |V| Knoten hat stets |V| - 1 Kanten.
- Wald
- Ein Wald ist ein unzusammenhängender, kreisfreier Graph.
- Jede Zusammenhangskomponente eines Waldes ist ein Baum.
Repräsentation von Graphen
Sei G = ( V, E ) gegeben und liege V in einer linearen Sortierung vor.
- Adjazenzmatrix
- Ein Graph kann durch eine Adjazenzmatrix repräsentiert werden, die soviele Zeilen und Spalten enthält, wie der Graph Knoten hat. Die Elemente der Adjazenzmatrix sind "1", falls eine Kante zwischen den zugehörigen Knoten existiert:
- Die Indizes der Matrix entsprechen also den Indizes der Knoten gemäß der gegebenen Sortierung. Im Falle eines ungerichteten Graphen ist die Adjazenzmatrix stets symmetrisch (d.h. es gilt ), bei einem gerichteten Graphen ist sie im allgemeinen unsymmetrisch.
Beispiel für einen ungerichteten Graphen:
v = { a,b,c,d } b d
| \ / |
| \/ |
| /\ |
| / \ |
a c
a b c d
-----------
(0 1 0 1) |a
A = (1 0 1 0) |b
(0 1 0 1) |c
(1 0 1 0) |d
Die Adjazenzmatrixdarstellung eignet sich besonders für dichte Graphen (d.h. wenn die Zahl der Kanten in O(|V|2) ist.
- Adjazenzlisten
- In der Adjazenzlistendarstellung wird der Graph als Liste von Knoten repräsentiert, die für jeden Knoten einen Eintrag enthält. Der Eintrag für jeden Knoten ist wiederum eine Liste, die die Nachbarknoten dieses Knotens enthält:
- graph = {adjazencyList(v) | v ∈ V}
- adjazencyList(v) = {v' ∈ V | (v, v') ∈ E}
In Python implementieren wir Adjazenzlisten zweckmäßig als Array von Arrays:
graph = [[...],[...],...,[...]] Adjazenzliste für Knoten => 0 1 n
Wenn wir bei dem Graphen oben die Knoten wie bei der Adjazenzmatrix indizieren (also a => 0, b => 1, c => 2, d => 3), erhalten wir die Adjazenzlistendarstellung:
graph = [[b, d], [a, c],[b, d], [a, c]]
Auf die Nachbarknoten eines durch seinen Index node gegebenen Knotens können wir also wie folgt zugreifen:
for neighbors in graph[node]:
... # do something with neighbor
Die Adjazenzlistendarstellung ist effizienter, wenn der Graph nicht dicht ist, so dass viele Einträge der Adjazenzmatrix Null wären.
- Transponierter Graph
- Den transponierten Graphen GT eines gerichteten Graphen G erhält man, wenn man alle Kantenrichtungen umkehrt.
Bei ungerichteten Graphen hat die Transposition offensichtlich keinen Effekt, weil alle Kanten bereits in beiden Richtungen vorhanden sind, so dass GT = G gilt. Bei gerichteten Graphen ist die Transposition dann einfach, wenn der Graph als Adjazenzmatrix implementiert ist, weil man einfach die transponierte Adjazenzmatrix verwenden muss (beachte, dass sich die Reihenfolge der Indizes umkehrt):
- AT = aji
Ist der Graph hingegen durch eine Adjazenzliste repräsentiert, muss etwas mehr Aufwand getrieben werden:
def transpose(graph):
gt = [[] for k in graph] # zunächst leere Adjazenzlisten von GT
for node in range(len(graph)):
for neighbor in graph[node]:
gt[neighbor].append(node) # füge die umgekehrte Kante in GT ein
return gt
Durchlaufen von Graphen (Graph Traversal)
Wir betrachten zunächst ungerichtete Graphen mit V Knoten und E Kanten. Eine grundlegende Aufgabe in diesen Graphen besteht darin, alle Knoten in einer bestimmten Reihenfolge genau einmal zu besuchen. Hierbei darf man sich von einem gegebenen Startknoten aus nur entlang der Kanten des Graphen bewegen. Die beim Traversieren benutzen Kanten bilden einen Baum, dessen Wurzel der Startknoten ist und der den gesamten Graphen aufspannt, falls der Graph zusammenhängend ist. (Beweis: Da jeder Knoten nur einmal besucht wird, gibt es für jeden besuchten Knoten [mit Ausnahme des Startknotens] genau eine eingehende Kante. Ist der Graph zusammenhängend, wird jeder Knoten tatsächlich erreicht und es gibt genau (V-1) Kanten, exakt soviele wie für einen Baum mit V Knoten notwendig sind.) Ist der Graph nicht zusammenhängend, wird jeder zusammenhängende Teilgraph (jede Zusammenhangskomponente) getrennt traversiert, und man erhält einen sogenannten Wald mit einem Baum pro Zusammenhangskomponente. Die beiden grundlegenden Traversierungsmethoden Tiefensuche und Breitensuche werden im folgenden vorgestellt.
Tiefensuche in Graphen (Depth First Search, DFS)
Die Idee der Tiefensuche besteht darin, jeden gefundenen Knoten sofort über die erste Kante wieder zu verlassen, die zu einem noch nicht besuchten Knoten führt. Man findet dadruch schnell einen möglichst langen Pfad durch den Graphen, und der Traversierungs-Baum wird zunächst in die Tiefe verfolgt, daher der Name des Verfahrens. Hat ein Knoten keine unbesuchten Nachbarknoten mehr, geht man im Baum zurück (sogenanntes back tracking), bis man einen Knoten findet, der noch eine unbesuchte Nachbarn besitzt, und traversiert diese nach dem gleichen Muster. Gibt es gar keine unbesuchten Knoten mehr, kehrt die Suche zum Startknoten zurück und endet dort.
Wenn der Graph als Adjazenzliste gegeben ist, implementiert man die Tiefensuche zweckmäßig rekursiv:
def dfs(graph, startnode):
visited = [None]*len(graph) # Flags, welche Knoten bereits besucht wurden
def visit(node): # rekursive Hilfsfunktion, die den gegebenen Knoten und dessen Nachbarn besucht
if visited[node] is None: # Besuche node, wenn er noch nicht besucht wurde
visited[node] = True # Markiere node als besucht
print node # Ausgabe der Knotennummer - pre-order
for neighbor in graph[node]: # Besuche rekursiv die Nachbarn
visit(neighbor)
visit(startnode)
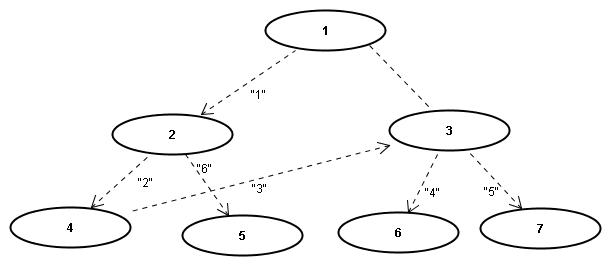
Ausgabe für den Graphen in diesem Bild (es handelt sich um einen ungerichteten Graphen, die Pfeile symbolisieren nur die Suchrichtung beim Traversal):
>>> dfs(graph, 1) 1 2 4 3 6 7 5
In dieser Version des Algorithmus werden die Knotennummern ausgegeben, bevor die Nachbarknoten besucht werden. Man bezeichnet die resultierende Sortierung der Knoten als pre-order oder als discovery order. Alternativ kann man die Knotennummern erst ausgeben, nachdem alle Nachbarn besucht wurden, also auf dem Rückweg der Rekursion. In diesem Fall spricht man von post-order oder finishing order:
def dfs(graph, startnode):
visited = [None]*len(graph) # Flags, welche Knoten bereits besucht wurden
def visit(node): # rekursive Hilfsfunktion, die den gegebenen Knoten und dessen Nachbarn besucht
if visited[node] is None: # Besuche node, wenn er noch nicht besucht wurde
visited[node] = True # Markiere node als besucht
for neighbor in graph[node]: # Besuche rekursiv die Nachbarn
visit(neighbor)
print node # Ausgabe der Knotennummer - post-order
visit(startnode)
Es ergibt sich jetzt die Ausgabe:
>>> dfs(graph, 1) 6 7 3 4 5 2 1
In realem Code ersetzt man die print-Ausgaben natürlich durch anwendungsspezifische Aktionen und Berechnungen. Einige Anwendungen sind uns im Kapitel Suchen bereits begegnet.
- Anwendungen der Pre-Order Traversierung
- Kopieren eines Graphen: kopiere zuerst den besuchten Knoten, dann seine Nachbarn und die dazugehörigen Kanten (sowie die Kanten zu bereits besuchten Knoten, die in der Grundversion der Tiefensuche ignoriert werden).
- Bestimmen der Zusammenhangskomponenten eines Graphen (siehe unten)
- In einem Zeichenprogramm: fülle eine Region mit einer Farbe ("flood fill"). Dabei ist jedes Pixel ein Knoten des Graphen und wird mit seinen 4 Nachbarpixceln verbunden. Die Tiefensuche startet bei der Mausposition und endet am Rand des betreffendcen Gebiets.
- Falls der Graph ein Baum ist: bestimme den Abstand jedes Knotens von der Wurzel
- Falls der Graph ein Parse-Baum ist, wobei innere Knoten Funktionsaufrufe, Kindknoten Funktionsargumente, und Blattknoten Werte repräsentieren: drucke den zugehörigen Ausdruck aus (also immer zuerst den Funktionsnamen, dann die Argumente, die wiederum geschachtelte Funktionsaufrufe sein können).
- Anwendungen der Post-Order Traversierung
- Löschen eines Graphen: lösche zuerst die Nachbarn, dann den Knoten selbst
- Bestimmen einer topologischen Sortierung eines azyklischen gerichteten Graphens (siehe unten)
- Falls der Graph ein Baum ist: bestimme den Abstand jedes Knotens von den Blättern (also die Tiefe des Baumes, siehe Übung 5)
- Falls der Graph ein Parse-Baum ist: führe die zugehörige Berechnung aus (d.h. berechne zuerst die geschachtelten inneren Funktionen, dann mit diesen Ergebnissen die nächst äußeren usw., siehe Übung 5).
- Anwendungen, die Pre- und Post-Order benötigen
- Weg aus einem Labyrinth: die Pre-Order dokumentiert die Suche nach dem Weg, die Post-Order zeigt den Rückweg aus Sackgassen (siehe Übung 9).
Im Spezialfall, wenn der Graph ein Binärbaum ist, unterscheidet man noch eine dritte Variante der Traversierung, nämlich die in-order Traversierung. In diesem Fall behandelt man den Vaterknoten nach den linken, aber vor den rechten Kindern. Diese Reihenfolge wird beim Tree Sort Algorithmus verwendet. Diese Sortierung verwendet man auch, wenn man einen Parse-Baum mit binären Operatoren (statt Funktionsaufrufen) ausgeben will, siehe Übung 5.
Eine nützliche Erweiterung der Tiefensuche besteht darin, im Array visited nicht nur zu dokumentieren, dass ein Knoten bereits besucht wurde, sondern auch, von welchem Knoten aus man den jeweiligen Knoten zuerst erreicht hat. Im entstehenden Tiefensuchbaum ist dies gerade der Vaterknoten, weshalb wir das Array zweckmäßigerweise in parents umbenennen. Für den Startknoten, also die Wurzel des Baumes, wählen wir die Konvention, dass er sein eigener Vaterknoten ist (die Konvention, dafür den Wert None zu verwenden, scheidet aus, weil dies bereits die Tatsache signalisiert, dass ein Knoten noch nicht besucht wurde):
def dfs(graph, startnode):
parents = [None]*len(graph) # Registriere für jeden Knoten den Vaterknoten im Tiefensuchbaum
def visit(node, parent): # rekursive Hilfsfunktion
if visited[node] is None: # Besuche node, wenn er noch nicht besucht wurde
visited[node] = parent # Markiere node als besucht und speichere seinen Vaterknoten
for neighbor in graph[node]: # Besuche rekursiv die Nachbarn ...
visit(neighbor, node) # ... wobei node zu deren Vaterknoten wird
visit(startnode, startnode) # Konvention für Wurzel: startnode ist sein eigener Vater
return parents # Rückgabe des berechneten Tiefensuch-Baums
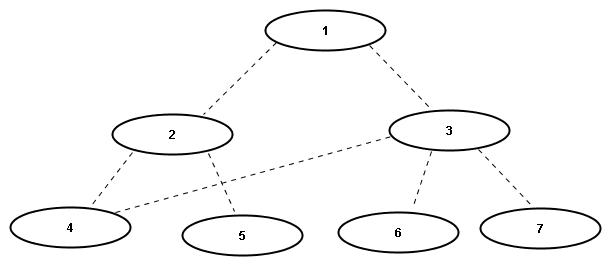
Die Ausgabe für den obigen Beispielgraphen lautet:
Knotennummer | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 --------------+-----+-----+-----+-----+-----+-----+-----+----- Vaterknoten | None| 1 | 1 | 4 | 2 | 2 | 3 | 3
Dabei ist die Knotennummer der Index im Array parents, und der Vaterknoten ist der dazugehörige Arrayeintrag. Beachte, dass Knoten 0 in diesem Graphen nicht existiert, daher ist sein Eintrag None. Per Konvention hat der Wurzelknoten 1 sich selbst als Vater.
Breitensuche in Graphen (Breadth First Search, BFS)
Im Gegensatz zur Tiefensuche werden bei der Breitensuche alle Nachbarnknoten abgearbeitet, bevor man rekursiv deren Nachbarn besucht. Man betrachtet somit zuerst alle Knoten, die den Abstand 1 von Startknoten haben, dann diejenigen mit dem Abstand 2 usw. Diese Reihenfolge bezeichnet man als level-order. Wir sind ihr beispielsweise in Übung 6 begegnet, als die ersten 7 Ebenen eines Treap ausgegeben werden sollten. Man implementiert Breitensuche zweckmäßig mit Hilfe einer Queue, die die Knoten in First In - First Out - Reihenfolge bearbeitet. Eine geeignete Datenstruktur hierfür ist die Klasse deque aus dem Python-Modul collections (eine Deque implementiert sowohl die Funktionalität einer Queue wie auch die eines Stacks, siehe Übung 3):
from collections import deque
def bfs(graph, startnode)
visited = [None]*len(graph) # Flags, welche Knoten bereits besucht wurden
q = deque() # Queue für die zu besuchenden Knoten
q.append(startnode) # Startknoten in die Queue einfügen
while len(q) > 0: # Solange es noch unbesuchte Knoten gibt
node = q.popleft() # Knoten aus der Queue nehmen (first in - first out)
if visited[node] is None: # Falls node noch nicht (auf einem anderen Weg) besucht wurde
visited[node] = True # Markiere node als besucht
print node # Drucke Knotennummer
for neighbor in graph[node]: # Füge Nachbarn in die Queue ein
q.append(neighbor)
Der Aufruf dieser Funktion liefert die Knoten des obigen Graphens ebenenweise, also zufällig genau in der Reihenfolge der Knotennummern:
>>> bfs(graph, 1) 1 2 3 4 5 6 7
Neben der ebenenweisen Ausgabe hat die Breitensuche viele weitere wichtige Anwendungen, z.B. beim Testen, ob ein gegebener Graph bi-partit ist (siehe WikiPedia), sowie bei der Suche nach kürzesten Wegen (siehe unten) und kürzesten Zyklen.
Weitere Anwendungen der Tiefensuche
Die Tiefensuche hat zahlreiche Anwendungen, wobei der grundlegende Algorithmus immer wieder leicht modifiziert und an die jeweilige Aufgabe angepasst wird. Wir beschreiben im folgenden einige Beispiele.
Damenproblem
Tiefensuche wird häufig verwendet, um systematisch nach der Lösung eines logischen Rätsels (oder allgemeiner nach der Lösung eines diskreten Optimierungsproblems) zu suchen. Besonders anschaulich hierfür ist das Damenproblem. Die Aufgabe besteht darin, Damen auf einem Schachbrett der Größe so zu platzieren, dass sie sich (nach den üblichen Schach-Regeln) nicht gegenseitig schlagen können. Das folgende Diagramm zeigt eine Lösung für den Fall . Die Positionen der Damen werden dabei wie üblich durch die Angabe der Spalte (Linie) mit Buchstaben und der Zeile (Reihe) mit Zahlen kodiert, hier also A2, B4, C1, D3:
--------------- | | X | | | 4 |---|---|---|---| | | | | X | 3 |---|---|---|---| | X | | | | 2 |---|---|---|---| | | | X | | 1 --------------- A B C D
Um das Problem systematisch zu lösen, konstruieren wir einen gerichteten Graphen, dessen Knoten die möglichen Positionen der Damen kodieren. Wir verbinden Knoten, die zu benachbarten Linien gehören, genau dann mit einer Kante, wenn die zugehörigen Positionen kompatibel sind, also wenn sich die dort positionierten Damen nicht schlagen können. Der resultierende Graph für hat folgende Gestalt:
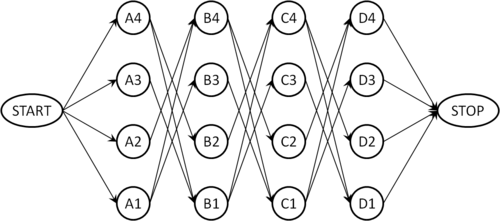
Knoten, die zur selben Reihe oder Linie gehören, sind beispielsweise nicht direkt verbunden, weil zwei Damen niemals in derselben Linie oder Reihe stehen dürfen. Um eine erlaubte Konfiguration zu finden, verwenden wir nun eine angepasste Version der Tiefensuche: Wir beginnen die Suche beim Knoten START. Sobald wir den Knoten STOP erreichen, beenden wir die Suche und lesen die Lösung am gerade gefundenen Weg von Start nach Stop ab. Zwei kleine Modifikationen des Grundalgorithmus stellen sicher, dass die Bedingungen der Aufgabe eingehalten werden: Wir dürfen bei der Tiefensuche nur dann zu einem Nachbarn weitergehen, wenn die betreffende Position mit allen im Pfad bereits gesetzten Positionen kompatibel ist, andernfalls ist diese Kante tabu. Landen wir aufgrund dieser Regel in einer Sackgasse (also in einem Knoten, wo keine der ausgehenden Kanten erlaubt ist), müssen wir zur nächsten erlaubten Abzweigung zurückgehen (Backtracking). Beim Zurückgehen müssen wir das parent-Flag wieder auf None zurücksetzen, weil der betreffende Knoten ja möglicherweise auf einem anderen erlaubten Weg erreichbar ist.
Der folgende Graph zeigt einen solchen Fall: Wir haben zwei Damen auf die Felder A1 und B3 positioniert (grüne Pfeile). Die einzig ausgehende Kante von B3 führt zum Knoten C1, welcher aber mit der Position A1 inkompatibel ist, so dass diese Kante nicht verwendet werden darf (roter Pfeil). Das Backtracking muss jetzt zu Knoten A1 zurückgehen (dabei wird das parent-Flag von B3 wieder auf None gesetzt), weil A1 mit der Kante nach B4 eine weitere Option hat, die geprüft werden muss (die allerdings hier auch nicht zum Ziel führt).
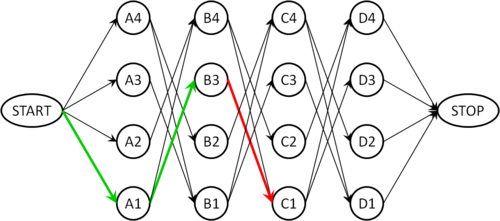
Nach einigen weiteren Sackgassen findet man schließlich den Pfad A2, B4, C1, D3, der im folgenden Graphen grün markiert ist und der obigen Lösung entspricht:
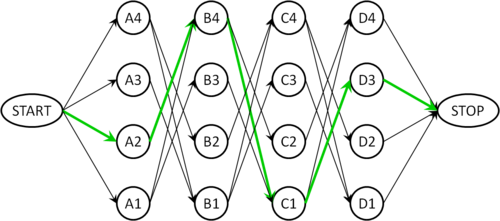
Test, ob ein ungerichteter Graph azyklisch ist
Ein zusammenhängender ungerichteter Graph ist azyklisch (also ein Baum) genau dann, wenn es nur einen möglichen Weg von jedem Knoten zu jedem anderen gibt. (Bei gerichteten Graphen sind die Verhältnisse komplizierter. Wir behandeln dies weiter unten.) Das kann man mittels Tiefensuche leicht feststellen: Die Kante, über die wir einen Knoten erstmals erreichen, ist eine Baumkante des Tiefensuchbaums. Erreichen wir einen bereits besuchten Knoten nochmals über eine andere Kante, haben wir einen Zyklus gefunden. Dabei müssen wir allerdings beachten, dass in einem ungerichteten Graphen jede Baumkante zweimal gefunden wird, einmal in Richtung vom Vater zum Kind und einmal in umgekehrter Richtung. Im zweiten Fall endet die Kante zwar in einem bereits besuchten Knoten (dem Vater), aber es entsteht dadurch kein Zyklus. Den Vaterknoten müssen wir deshalb überspringen, wenn wir über die Nachbarn iterieren:
def undirected_cycle_test(graph): # Annahme: der Graph ist zusammenhängend
# (andernfalls führe den Algorithmus für jede Zusammenhangskomponente aus)
visited = [None]*len(graph) # Flags für bereits besuchte Knoten
def visit(node, from_node): # rekursive Hilfsfunktion: gibt True zurück, wenn Zyklus gefunden wurde
if visited[node] is None: # wenn node noch nicht besucht wurde
visited[node] = True # markiere node als besucht
for neighbor in graph[node]: # besuche die Nachbarn ...
if neighbor == from_node: # ... aber überspringe den Vaterknoten
continue
if visit(neighbor, node): # ... signalisiere, wenn rekursiv ein Zyklus gefunden wurde
return True
return False # kein Zyklus gefunden
else:
return True # Knoten schon besucht => Zyklus
startnode = 0 # starte bei beliebigem Knoten (hier: Knoten 0)
return visit(startnode, startnode) # gebe True zurück, wenn ein Zyklus gefunden wurde
Wenn wir einen Zyklus finden, wird das weitere Traversieren das Graphen abgebrochen, denn ein Graph, der einmal zyklisch war, kann später nicht wieder azyklisch werden. Die notwendige Modifikation für unzusammenhängende Graphen erfolgt analog zum Algorithmus für die Detektion von Zusammenhangskomponenten, der im nächsten Abschnitt beschrieben wird.
Finden von Zusammenhangskomponenten
Das Auffinden und Markieren von Zusammenhangskomponenten (also maximalen zusammenhängenden Teilgraphen) ist eine grundlegende Aufgabe in ungerichteten, unzusammenhängenden Graphen (bei gerichteten Graphen sind die Verhältnisse wiederum komplizierter, siehe unten). Zwei Knoten u und v gehören zur selben Zusammenhangskomponente genau dann, wenn es einen Pfad von u nach v gibt (da der Graph ungerichtet ist, gibt es dann auch einen Pfad von v nach u). Man sagt auch, dass "v von u aus erreichbar" ist. Unzusammenhängende Graphen entstehen in der Praxis häufig, wenn die Kanten gewisse Relationen zwischen den Knoten kodieren:
- Wenn die Knoten Städte sind und die Kanten Straßen, sind diejenigen Städte in einer Zusammenhangskomponente, die per Auto von einander erreichbar sind. Unzusammenhängende Graphen entstehen hier beispielsweise, wenn eine Insel nicht durch eine Brücke erschlossen ist, wenn Grenzen gesperrt sind oder wenn ein Gebirge zu unwegsam ist, um Straßen zu bauen.
- Wenn Knoten Personen sind, und Kanten die Eltern-Kind-Relation beschreiben, so umfasst jede Zusammenhangskomponenten die Verwandten (auch wenn sie nur über viele "Ecken" verwandt sind).
- In der Bildverarbeitung entsprechen Knoten den Pixeln, und dieselben werden durch eine Kante verbunden, wenn sie zum selben Objekt gehören. Die Zusammenhangskomponenten entsprechen somit den Objekten im Bild (siehe Übungsaufgabe).
Die Zusammenhangskomponenten bilden eine Äquivalenzrelation. Folglich kann für jede Komponente ein Reprässentant bestimmt werden, der sogenannte "Anker". Kennt jeder Knoten seinen Anker, ist das Problem der Zusammenhangskomponenten gelöst.
Lösung mittels Tiefensuche
Unser erster Ansatz ist, den Anker mit Hilfe der Tiefensuche zu finden. Anstelle des Arrays visited verwenden wir diesmal ein Array anchors, das für jeden Knoten die Knotennummer des zugehörigen Ankers angibt, oder None, wenn der Knoten noch nicht besucht wurde. Dabei verwenden wir wieder die Konvention, dass Anker auf sich selbst zeigen. Für viele Anwendungen ist es außerdem (oder stattdessen) zweckmäßig, die Zusammenhangskomponenten mit einer laufenden Nummer, einem sogenannten Label, durchzuzählen. Dann kann man zusätzliche Informationen zu jeder Komponente (beispielsweise deren Größe) einfach in einem Array speichern, das über die Labels indexiert wird. Die folgende Version der Tiefensuche bestimmt sowohl die Anker als auch die Labels für jeden Knoten:
def connectedComponents(graph):
anchors = [None] * len(graph) # Array für Anker jedes Knotens
labels = [None] * len(graph) # Array für Label jedes Knotens
def visit(node, anchor):
"""anchor ist der Anker der aktuellen ZK"""
if anchors[node] is None: # wenn node noch nicht besucht wurde:
anchors[node] = anchor # setze seinen Anker
labels[node] = labels[anchor] # und sein Label
for neighbor in graph[node]: # und besuche die Nachbarn
visit(neighbor, anchor)
current_label = 0 # Zählung der ZK beginnt bei 0
for node in xrange(len(graph)):
if anchors[node] is None: # Anker noch nicht bekannt => neue ZK gefunden
labels[node] = current_label # Label des Ankers setzen
visit(node, node) # Knoten der neuen ZK rekursiv suchen
current_label += 1 # Label für die nächste ZK hochzählen
return anchors, labels
Interessant ist hier die Schleife über alle Knoten des Graphen am Ende des Algorithmus, die bei den bisherigen Versionen der Tiefensuche nicht vorhanden war. Um ihre Funktionsweise zu verstehen, nehmen wir für den Moment an, dass der Graph zusammenhängend ist. Dann findet diese Schleife den ersten Knoten des Graphen und führt die Tiefensuche mit diesem Knoten als Startknoten aus. Sobald die Rekursion zurückkehrt, sind alle Knoten des Graphen besucht (weil der Graph ja zusammenhängend war), so dass die Schleife alle weiteren Knoten überspringt (die if-Anweisung liefert für keinen weiteren Knoten True). Bei unzusammenhängenden Graphen dagegen erreicht die Tiefensuche nur die Knoten derselben Komponente, die im weiteren Verlauf der Schleife übersprungen werden. Findet die if-Anweisung jetzt einen noch nicht besuchten Knoten, muss dieser folglich in einer neuen Komponente liegen. Wir verwenden diesen Knoten als Anker und bestimmen die übrigen Knoten dieser Komponente wiederum mit Tiefensuche.
- Beispiel: ... under construction
Man erkennt, dass die Tiefensuche nach dem Anlagerungsprinzip vorgeht: Beginnend vom einem Startknoten (dem Anker) werden die Knoten der aktuellen Komponente nach und nach an den Tiefensuchbaum angehangen. Erst, wenn nichts mehr angelagert werden kann, geht der Algorithmus zur nächsten Komponente über.
Lösung mittels Union-Find-Algorithmus
Im Gegensatz zum Anlagerungsprinzip sucht der Union-Find-Algorithmus die Zusammenhangskomponenten mit dem Verschmelzungsprinzip: Eingangs wird jeder Knoten als ein Teilgraph für sich betrachtet. Dann iteriert man über alle Kanten und verbindet deren Endknoten jeweils zu einem gemeinsamen Teilgraphen (falls die beiden Enden einer Kante bereits im selben Teilgraphen liegen, wird diese Kante ignoriert). Solange noch Kanten vorhanden sind, werden dadurch immer wieder Teilgraphen in größere Teilgraphen verschmolzen. Am Ende bleiben die maximalen zusammenhängenden Teilgraphen (also gerade die Zusammenhangskomponenten) übrig. Dieser Algorithmus kommt ohne Tiefensuche aus und ist daher in der Praxis oft schneller, allerdings auch etwas komplizierter zu implementieren.
Der Schlüssel des Algorithmus ist eine Funktion findAnchor(), die zu jedem Knoten den aktuellen Anker sucht. Der Anker existiert immer, da jeder Knoten von Anfang an zu einem Teilgraphen gehört (auch wenn dieser anfangs trivial ist und nur aus dem Knoten selbst besteht). Die Verschmelzung wird realisiert, indem der Anker des einen Teilgraphen seine Rolle verliert und stattdessen der Anker des anderen Teilgraphen eingesetzt wird.
Zur Verwaltung der Anker verwenden wir wieder ein Array anchors mit der Konvention, dass ein Anker auf sich selbst verweist. Allerdings wäre es zu teuer, wenn man bei jeder Verschmelzung alle Einträge der beteiligten Knoten aktualisieren müsste, da jeder Knoten im Laufe des Algorithmus mehrmals einen neuen Anker bekommt. Statt dessen definiert man Anker rekursiv: Verweist ein Knoten auf einen Anker, der mittlerweile diese Rolle verloren hat, folgt man dem Verweis von diesem Knoten (dem ehemaligen Anker) weiter, bis man einen tatsächlichen Anker gefunden hat - erkennbar daran, dass er auf sich selbst verweist. Die Suchfunktion kann folgendermassen implementiert werden:
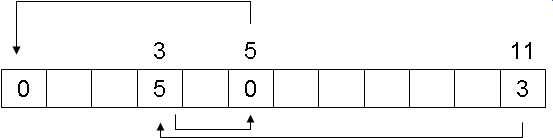
def findAnchor(anchors, node):
while node != anchors[node]: # wenn node kein Anker ist
node = anchors[node] # ... verfolge die Ankerkette weiter
return node
Allerdings kann diese Kette im Laufe vieler Verschmelzungen sehr lang werden, so dass das Verfolgen der Kette teuer wird. Man vermeidet dies durch die sogenannte Pfadkompression: Immer, wenn man den Anker gefunden hat, altualisiert man den Eintrag am Anfang der Kette. Die Funktion findAnchor() wird dadurch nur wenig komplizierter:
def findAnchor(anchors, node):
start = node # wir merken uns den Anfang der Kette
while node != anchors[node]: # wenn node kein Anker ist
node = anchors[node] # ... verfolge die Ankerkette weiter
anchors[start] = node # Pfadkompression: aktualisiere den Eintrag am Anfang der Kette
return node
Man kann zeigen, dass die Ankersuche mit Pfadkompression zu einer fast konstanten amortisierten Laufzeit pro Aufruf führt.
Um mit jeder Kante des (ungerichteten) Graphen nur maximal einmal eine Verschmelzung durchzuführen, betrachten wir jede Kante nur in der Richtung von der kleineren zur größeren Knotennummer, die umgekehrte Richtung wird ignoriert. Außerdem ist es zweckmäßig, bei jeder Verschmelzung den Anker mit der kleineren Knotennummer als neuen Anker zu übernehmen. Dann gilt für jede Zusammenhangskomponente, dass gerade der Knoten mit der kleinsten Knotennummer der Anker ist (genau wie bei der Lösung mittels Tiefensuche), was die weitere Analyse vereinfacht, z.B. die Zuordnung der Labels zu den Komponenten am Ende des Algorithmus.
def unionFindConnectedComponents(graph):
anchors = range(len(graph)) # Initialisierung: jeder Knoten ist sein eigener Anker
for node in xrange(len(graph)): # iteriere über alle Knoten
for neighbor in graph[node]: # ... und über deren ausgehende Kanten
if neighbor < node: # ignoriere Kanten, die in falscher Richtung verlaufen
continue
# hier landen wir für jede Kante des Graphen genau einmal
a1 = findAnchor(anchors, node) # finde Anker ...
a2 = findAnchor(anchors, neighbor) # ... der beiden Endknoten
if a1 < a2: # Verschmelze die beiden Teilgraphen
anchors[a2] = a1 # (verwende den kleineren der beiden Anker als Anker des
elif a2 < a1: # entstehenden Teilgraphen. Falls node und neighbor
anchors[a1] = a2 # den gleichen Anker haben, waren sie bereits im gleichen
# Teilgraphen, und es passiert hier nichts.)
# Bestimme jetzt noch die Labels die Komponenten
labels = [None]*len(graph)
current_label = 0 # die Zählung beginnt bei 0
for node in xrange(len(graph)):
a = findAnchor(anchors, node)
if a == node: # node ist ein Anker
labels[a] = current_label # => beginne eine neue Komponente
current_label += 1 # und zähle Label für die nächste ZK hoch
else:
labels[node] = labels[a] # node ist kein Anker => setzte das Label des Ankers
# (wir wissen, dass labels[a] bereits gesetzt ist, weil
# der Anker immer der Knoten mit der kleinsten Nummer ist)
return anchors, labels
- Beispiel: ... under construction
Kürzeste Wege (Pfade)
Eine weitere grundlegende Aufgabe in Graphen ist die Bestimmung eines kürzesten Weges zwischen zwei gegebenen Knoten. Dies hat offensichtliche Anwendungen bei Routenplanern und Navigationssystemen und ist darüber hinaus wichtiger Bestandteil anderer Algorithmen, z.B. bei der Berechnung eines maximalen Flusses mit der Methode von Edmonds und Karp.
Im Fall eines ungewichteten Graphen ist die Länge eines Weges einfach durch die Anzahl der durchlaufenen Kanten definiert. Daraus folgt, dass kürzeste Pfade mit einer leicht angepassten Version der Breitensuche gefunden werden können: Aufgrund des first in-first out-Verhaltens der Queue betrachtet die Breitensuche alle (erreichbaren) Knoten in der Reihenfolge ihres Abstandes vom Startknoten. Wenn wir den Zielknoten zum ersten Mal erreichen, und der gerade gefundene Weg vom Start zum Ziel hat die Länge L, muss dies der kürzeste Weg sein: Alle möglichen Wege der Länge L' < L hat die Breitensuche ja bereits betrachtet, ohne dass dabei der Zielknoten erreicht wurde. Daraus folgt übrigens eine allgemeine Eigenschaft aller Algorithmen für kürzeste Wege: Wenn der kürzeste Weg vom Start zum Ziel die Länge L hat, finden diese Algorithmen als Nebenprodukt auch die kürzesten Wege zu allen Knoten, für die L' < L gilt.
Um den Algorithmus zu implementieren, passen wir die Breitensuche so an, dass anstelle des Arrays visited ein Array parents verwendet wird, das für jeden besuchten Knoten den Vaterknoten im Breitensuchbaum speichert. Durch Rückverfolgen der parent-Kette können wir den Pfad vom Ziel zum Start rekonstruieren, und durch Umdrehen der Reihenfolge erhalten wir den gesuchten Pfad vom Start zum Ziel.
- Definition: gewichteter Graph
Jeder Kante e ist eine reelle oder natürliche Zahl we zugeordnet (wird auch als Kantengewicht bezeichnet).
z.B.
- Abstand der Anfangs- und Endknoten
- Durchflusskapazität eines Rohres (für max-Flussprobleme)
- Wechselkurse (Darstellung in einem gerichteten Graph, da jede Kante auch eine Richtung hat. Die Knoten sind die Währungen, die Kanten sind die Wechselkurse. Auf diese Weise lassen sich unterschiedliche Wechselkurse + Bankgebühren darstellen.)
- Definition: Problem des kürzesten Weges
Sei P die Menge aller Wege von u nach v
Puv = {u_v}
und der Weg gegeben durch
u → x1 → x2 → ... → v
dann sind die Kosten eines Weges definiert durch
Kosten (Puv) = we
- gesucht: Pfad u_v, so dass Kosten (u_v) minimal sind
- Lösung: Algorithmus von Dijkstra
Algorithmus von Dijkstra
Edsger Wybe Dijkstra
geb. 11. Mai 1930 in Rotterdam
ges. 06. August 2002
Dijkstra war ein niederländischer Informatiker und Wegbereiter der strukturierten Programmierung. 1972 erhielt er für seine Leistung in der Technik und Kunst der Programmiersprachen den Turing Award, der jährlich von der Association for Computing Machinery (ACM) an Personen verliehen wird, die sich besonders um die Entwicklung der Informatik verdient gemacht haben. Zu seinen Beiträgen zur Informatik gehören unter anderem der Dijkstra-Algorithmus zur Berechnung des kürzesten Weges in einem Graphen sowie eine Abhandlung über den go-to-Befehl und warum er nicht benutzt werden sollte. Der go-to-Befehl war in den 60er und 70er Jahren weit verbreitet, führte aber zu Spaghetti-Code. In seinem berühmten Paper "A Case against the GO TO Statement"[2], das als Brief mit dem Titel "Go-to statement considered harmful" veröffentlicht wurde, argumentiert Dijkstra, dass es umso schwieriger ist, dem Quellcode eines Programmes zu folgen, je mehr go-to-Befehle darin enthalten sind und zeigt, dass man auch ohne diesen Befehl gute Programme schreiben kann.
Algorithmus
import heapq # heapq ist ein Modul von Python
def dijkstra(graph, start, ziel): # graph: gewichtete Adjazenzliste
heap = []
visited = [None]*len(graph)
visited[start] = start
for neighbor in graph[start]:
heapq.heappush(heap, (neighbor[1], start, neighbor[0])) # neighbor[1]:Kantengewicht,neighbor[0]:Endpunkt d. K.
while len(heap) > 0: # solange der heap nicht leer ist
w, fromNode, node = heapq.heappop(heap)
if visited[node] is not None: # wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
continue
visited[node] = fromNode # baue Vorgänger-Baum
if node == ziel: # da der heap noch nicht leer ist, wird an dieser Stelle ein break benötigt
break
for neighbor in graph[node]:
if visited[neighbor[0]] is not None: # wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
continue
heapq.heappush(heap, (neighbor[1]+w, node, neighbor[0]))
bestPath = []
t = ziel
while t != visited[t]: # Array wird durchlaufen bis der Anker des Pfades gefunden ist, vgl. Union-Search
bestPath.append(t)
t=visited[t]
bestPath.append(start)
return bestPath # bestPath.reverse()
Anmerkungen zum Code:
- der graph ist eine gewichtete Adjazenzliste
| Knoten | 0 | → | Endknoten | → | Endknoten | (Nr. der Nachbarn des Knoten 0) |
| 1 | Gewicht | Gewicht | (Gewicht der jeweiligen Kante) | |||
| 2 | ||||||
| 3 |
- Eingabe z.B.:
| Knoten | 0 | → | (1, 0.3) | (3, 0.1) | (5, 1.2) | |
| 1 | → | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
- heapq() verwendet den 1. Eintrag des Tupels zum sortieren des heap
Prinzip des Dijkstra-Algorithmus
- Algorithmus ist Tiefensuche mit Prioritätswarteschlange (Heap) statt eines Stapelspeichers (Stack) → vgl. Übung 8
- Die Prioritätswarteschlange speichert die kürzesten Wege, die bereits gefunden worden sind.
- Wenn man die Prioritätswarteschlange (Heap) durch eine Warteschlange (Queue) ersetzt, erhält man Breitensuche.
- Wenn man die Prioritätswarteschlange (Heap) durch einen Stapelspeicher (Stack) ersetzt, erhält man Tiefensuche.
Beispiel
- An der Stelle "neighbor[1]" wird eine Zählvariable count eingefügt, die hoch (Breitensuche) oder runter (Tiefensuche) zählt.
- Die Gewichte werden hoch- oder runtergezählt, so wie die Kanten gesehen wurden.
- Wenn man rückwärts zählt (von 0 abziehen), werden die zuletzt hinzugefügten Kanten expandiert.
- Algorithmus von Dijkstra funktioniert nur für positive Kantengewichte
- we > 0
- Bei negativen Kantengewichten könnte es Zyklen geben, die negative Kosten für den ganzen Zyklus haben:
/\ 1. Durchlauf: Kosten -1
1 / \ -4 2. Durchlauf: Kosten -2
/____\ etc.
2
- Verwendung bei arbitragen Geschäften (Börsengeschäfte, die die Preis-, Kurs- und Zinsunterschiede auf verschiedenen Märkten ausnutzen):
- EURO wurden in YEN, YEN in DOLLAR gewechselt und das Geld hat sich dadurch vermehrt
- Für negative Kantengewichte verwendet man den Bellman-Ford-Allgorithmus, der allerdings langsamer ist, als der Dijkstra-Algorithmus.
Komplexität von Dijkstra
- Jeder Knoten wird höchstens 1x expandiert (Iteration über die Nachbarn des Knotens).
- Jeder Knoten kann mehrmals im Heap enthalten sein.
- Es sind aber höchstens E (Anzahl der Kanten) Heap-Einträge möglich, da jede Kante höchstens 1 Heap-Eintrag generiert (ein Knoten ist nur dann im Heap, wenn man ihn über eine Kante erreicht hat, die man vorher noch nicht besucht hatte). Deshalb können nie mehr Einträge im Heap sein, als es Kanten gibt. Die Komplexität von heappush(), heappop() ist
O(log E) = O(2 log v) = O(log v)
wenn alle Kanten einen Heap-Eintrag generiert haben.
- Die while-Schleife wird im schlimmsten Fall E mal durchlaufen, deshalb ist die Komplexität von Dijkstra O(E log v).
Korrektheit von Dijkstra
- Falls
visited[node] (Schleifen-Invariante von while) != None
ist, dann liefert Zurückverfolgen des Pfades von node nach start den kürzesten Pfad von start nach node (gilt für alle Knoten, für die das visited-Feld gesetzt ist).
- Induktionsanfang: visited[start] ist einziger not-None-Fall → Bedingung erfüllt
- Induktionsschritt: wenn visited[node] gesetzt wird, ist es ein kürzester Pfad
Indirekter Beweis
Set S = {node | visited[node] != None} (alle Knoten, von denen wir den kürzesten Pfad schon kennen)
- u ist der Knoten an der Spitze des Heaps
- fromNode S (ein Nachbar von node kommt erst dann in den Heap, wenn visited[node] vorher gesetzt wurde)
- falls u → fromNode → start kein kürzester Pfad wäre, müsste u's Vorgänger in V\S sein
- sei dieser Vorgänger x S, x u
- sei wx das Gewicht der Kante x → u, dann sind die Kosten für start nach u gleich
Kosten(start_u) = Kosten(start_x) + wx
- Annahme des indirekten Beweises:
Kosten(start_fromNode) + wfromNode
- Behauptung des indirekten Beweises:
Es gibt einen anderen Pfad x, so dass die Kosten von start nach x geringer sind
- Da aber gilt:
fromNode S und x S
- gilt (Induktionsvoraussetzung):
Kosten(start_fromNode) < Kosten(start_x)
- Falls Kosten(start_x) < Kosten(start_u) müsste x im Heap vor u kommen; daraus folgt, dass u nicht an der Spitze des Heaps sein kann
→ Widerspruch!
→ Die Behauptung, der Weg über x ist besser, kann nicht stimmen.
→ Korrektheit von Dijkstra ist somit bewiesen.
A*-Algorithmus - Wie kann man Dijkstra noch verbessern?
- Verbesserung von Dijkstra im typischen Fall, aber die Komplexität ist immer noch =(Elog v) im schlechtesten Fall (die Komplexität kann man nicht verbessern, aber die Laufzeit im typischen Fall).
- Schätzung für jeden Knoten für den restlichen Weg:
geschätzte Gesamtkosten: Kosten(start_node) + Restschätzung(node_ziel) (exakte Kosten werden durch Dijkstra ermittelt)
Idee:
- Sortiere den Heap nach geschätzten Gesamtkosten.
- Satz:
Falls jede Schätzung den exakten Weg unterschätzt, werden die gleichen Pfade gefunden, wie bei Dijkstra (also die korrekten kürzesten Pfade).
(Die Schätzung für den restlichen Weg muss man immer so einrichten, dass der tatsächliche Weg unterschätzt wird. Da keine Straße kürzer sein kann als die Luftlinie, ist die Luftlinie eine geeignete Annahme für A*.)
- Falls der falsche Pfad im Heap eher an die Spitze kommt als der richtige Pfad, findet der A*-Algorithmus den falschen Pfad.
- Wenn der Pfad zum Ziel an der Spitze des Heap ist, dann wird keine Restschätzung mehr benötigt, denn wenn der Zielknoten aus dem Heap herrauskommt, dann hat man die exakte Berechnung. Die Restschätzung ist in diesem Fall 0. Wenn die Schätzung zu klein ist, wird der exakte Weg immer größer sein und zuerst aus dem Heap herauskommen.

Minimaler Spannbaum
(engl.: minimum spanning tree; abgekürzt: MST)
- gegeben: gewichteter Graph, zusammenhängend
- gesucht: Untermenge , so dass minimal und G' zusammenhängend ist.
- G'definiert dann einen Baum, denn andernfalls könnte man verringern (eine Kante weglassen) ohne die Zusammenhangskomponente zu verletzen.
- Wenn der Graph nicht zusammenhängend ist, würde man den Spannbaum für jede Zusammenhangskomponente getrennt ausrechnen.
- Der MST ist ähnlich wie der Dijkstra-Algorithmus: Dort ist ein Pfad gesucht bei dem die Summe der Gewicht über den Pfad minimal ist.
- Beim MST suchen wir eine Lösung bei der die Summe der Gewichte über den ganzen Graphen minimal ist.
- Das Problem des MST ist nahe verwandt mit der Bestimmung der Zusammenhangskomponente, z.B. über den Tiefensuchbaum, wobei ein beliebiger Baum für die Zusammenhangskomponente und beim MST ein minimaler Baum gesucht ist.
- Anwendungen
- Wie verbindet man n Punkte mit möglichst wenigen (kurzen) Straßen (Eisenbahnen, Drähten (bei Schaltungen) usw.)?
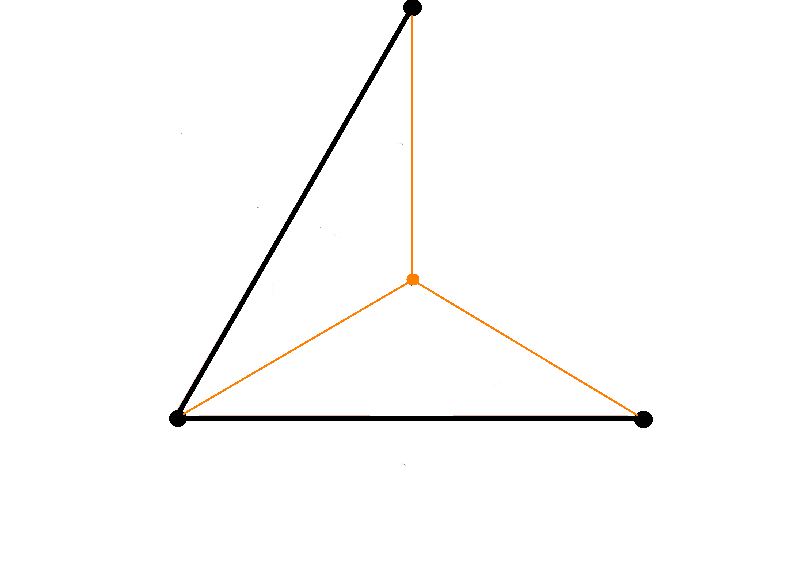
| MST minimale Verbindung (Abb.1) | MST = 2 (Länge = Kantengewicht)(Abb.2) |

|
|
- In der Praxis: Die Festlegung, dass man nur die gegebenen Punkte verwenden darf, ist eine ziemliche starke Einschränkung.
- Wenn man sich vorstellt, es sind drei Punkte gegeben, die als gleichseitiges Dreieck angeordnet sind, dann ist der MST (siehe Abb.2, schwarz gezeichnet) und hat die Länge 2. Man kann hier die Länge als Kantengewicht verwenden.
- Wenn es erlaubt ist zusätzliche Punkte einzufügen, dann kann man in der Mitte einen neuen Punkt setzen neuer MST (siehe Abb.2, orange gezeichnet).
- Höhe = , Schwerpunkt: teilt die Höhe des Dreiecks im Verhältnis 2:1; der Abstand von obersten Punkt bis zum neu eingeführten Punkt: , davon insgesamt 3 Stück, damit (gilt für den MST in orange eingezeichnet): MST = <br\>
- Damit ist der MST in orange kürzer als der schwarz gezeichnete MST. <br\>
Folgerung: MST kann kürzer werden, wenn man einen Punkt dazu nimmt.
- Umgekehrt kann der MST auch kürzer werden, wenn man einen Punkt aus dem Graphen entfernt, aber wie das Beipiel des gleichseitigen Dreiecks zeigt, ist dies nicht immer der Fall.
- Methode der zusätzlichen Punkteinfügung hat man früher beim Bahnstreckenbau verwendet. Durch Einführung eines Knotenpunktes kann die Streckenlänge verkürzt werden (Dreiecksungleichung).
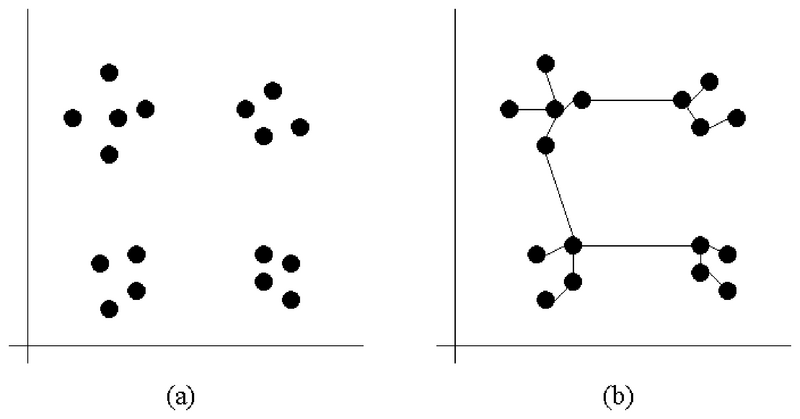
- Bestimmung von Datenclustern
- Daten (in der Abb.: Punkte) bilden Gruppen.
- In der Abbildung hat man 2 verschiedene Messungen gemacht (als x- und y-Achse aufgetragen), bspw. Größe und Gewicht von Personen. Für jede Person i wird ein Punkt an der Koordinate (Größei, Gewichti) gezeichnet (siehe Bild a). Dies bezeichnet man als Scatter Plot. Wenn bestimmte Wertkombinationen häufiger auftreten als andere, bilden sich mitunter Gruppen aus, bspw. eine Gruppe für "klein und schwer" etc.
- Durch Verbinden der Punkte mittels eines MST (siehe Abbildung (b)) sieht man, dass es kurze (innerhalb der Gruppen) und lange Kanten (zwischen den Gruppen) gibt.
- Wenn man geschickt eine Schwelle einführt und alle Kanten löscht, die länger sind als die Schwelle, dann bekommt man als Zusammenhangskomponente die einzelnen Gruppen.
Zwei Algorithmen für dieses Problem
(im Vergleich zu Algorithmen für die Zusammenhangskomponente nur leicht verbesserte Algorithmen)
Algorithmus von Prim
- Idee: starte an der Wurzel (willkürlich gewählter Knoten) und füge jeweils die günstigste Kante hinzu ( genau wie beim Dijsktra-Algorithmus, aber die Definitionen, welche Kante die günstigste ist, unterscheiden sich.)
import heapq def prim(graph): #Graphdatenstruktur ist wie bei Dijsktra heap = [] visited = [False]*len(graph) sum = 0 #wird später das Gewicht des Spannbaums sein r = [] #r ist die Lösung visited[0] = True #fixed for neighbor in graph[0]: #willkürlich 0 als Wurzel gewählt heapq.heappush(heap, (neighbor[1], 0, neighbor[0])) #Heap wird gefüllt while len(heap): wn, start, ziel = heapq.heappop(heap) if visited[ziel]: continue visited[ziel] = True #wenn visited noch nicht besetzt sum += wn #Addition des Gewichts der aktuellen Kante r.append([start, ziel]) #Kante wird an die Lsg. angehängt for neighbor in graph[ziel]: if visited[neighbor[0]]: continue heapq.heappush(heap, (neighbor[1], ziel, neighbor[0])) return sum, r
Algorithmus von Kruskal
Eine andere Vorgehensweise zur Bestimmung des minimalen Spannbaums besteht darin, einfach Kanten nacheinander hinzuzufügen und hierbei bei jedem Schritt die kürzeste Kante zu verwenden, die keinen Zyklus bildet. Anders ausgedrückt: Der Algorithmus beginnt mit N Bäumen; in (N-1) Schritten kombiniert er jeweils zwei Bäume (unter Verwendung der kürzesten möglichen Kante), bis nur noch ein Baum übrig bleibt. Der Algorithmus von J.Kruskal ist seit 1956 bekannt.
- Idee: wie beim Union-Find-Algorithmus für Zusammenhangskomponenten
- Behandle jeden Knoten als Baum für sich
- Fasse zwei Bäume zu einem neuen Baum zusammen
- für MST (im Unterschied zu Union-Find): betrachte dazu die Kanten in aufsteigender Reihenfolge der Gewichte
(priority queue; ignoriere Kanten zwischen Knoten, die sich bereits im gleichem Baum befinden, was sich leicht daran erkennen läßt, dass ihre Anker gleich sind)
- Algorithmus eignet sich besser für das Clusteringproblem, da der Schwellwert von vornerein über die Kantenlänge an den Algorithmus übergeben werden kann. Man hört mit dem Vereinigen auf, wenn die Kantenlänge den Schwellwert überschreitet.
- Es kann keine kürzere Kante als der Schwellwert mehr kommen, da die Kanten vorher sortiert worden sind.
Komplexität: gleich wie beim Dijkstra-Algorithmus, weil jede Kante höchstens einmal in den Heap kommt.
- Aufwand für Heap ist max. Einträge, da jede Kante nur einmal im Heap sein kann, d.h. Heap hat den Aufwand: , falls keine Mehrfachkanten vorhanden: und deshalb: log E < 2 log v.
- Daraus folgt, dass das dasselbe ist wie
=> geeignet für Übungsaufgabe
Problem des Handlungsreisenden
(engl.: Traveling Salesman Problem; abgekürzt: TSP)<br\> Wikipedia (de) (en)
- Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden.
- Hierbei soll ein Handlungsreisender nacheinander n Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden.
- Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen.
- gegeben: zusammenhängender, gewichteter Graph (oft vollständiger Graph)
- gesucht: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\>
- auch genannt: kürzester Hamiltonkreis
- - durch psychologische Experimente wurde herausgefunden, dass Menschen (in 2D) ungefähr proportionale Zeit zur Anzahl der Knoten brauchen, um einen guten Pfad zu finden, der typischerweise nur länger als der optimale Pfad ist<br\>
- vorgegeben: Startknoten (kann willkürlich gewählt werden), vollständiger Graph
- => v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger...
- also mögliche Wege in einem vollständigen Graphen
- Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird.
- Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität.
Approximationsalgorithmus
Für viele Probleme in der Praxis sind keine effizienten Algorithmen bekannt (NP-schwer). Diese (z.B. TSP) werden mit Approximationsalgorithmen berechnet, die effizient berechenbar sind, aber nicht unbedingt die optimale Lösung liefern. Beispielsweise ist es relativ einfach, eine Tour zu finden, die höchstens um den Faktor zwei länger ist als die optimale Tour. Die Methode beruht darauf, dass einfach der minimale Spannbaum ermittelt wird.
Approximationsalgorithmus für TSP<br\>
- TSP für n Knoten sei durch Abstandsmatrix D =
- gegeben (vollständiger Graph mit n Knoten, = Kosten der Kante (i,j)) <br\>
- gesucht: Rundreise mit minimalen Kosten. Dies ist NP-schwer!<br\>
- D erfüllt die Dreiecksungleichung <br\>
- Dies ist insbesondere dann erfüllt, wenn D die Abstände bezüglich einer Metrik darstellt oder D Abschluss einer beliebigen Abstandsmatrix C ist, d.h. : = Länge des kürzesten Weges (bzgl. C) von i nach j.
- Die ”Qualität”der Lösung mit einem Approximationsalgorithmus ist höchstens um einen konstanten Faktor schlechter ist als die des Optimums.
Systematisches Erzeugen aller Permutationen
- Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\>
- Trick: interpretiere jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\>
- Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst.
gegeben: zwei Wörter a, b der Länge n=len(a) bzw. m=len(b). Sei k = min(n,m) (im Spezialfall des Vergleichs von Permutationen gilt k = n = m)<br\> Mathematische Definition, wie die Wörter im Wörterbuch sortiert sind: <br\>
- <br\>
Algorithmus zur Erzeuguung aller Permutationen:
- beginne mit dem kleinsten Wort bezüglich der lexikographischen Ordnung => das ist das Wort, wo a aufsteigend sortiert ist
- definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt
Beispiel: Die folgenden Permutationen der Zahlen 1,2,3 sind lexikographisch geordnet
1 2 3 6 Permutationen, da 3! = 6 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 ----- 0 1 2 Position
Die lexikographische Ordnung wird deutlicher, wenn wir statt dessen die Buchstaben a,b,c verwenden:
abc acb bac bca cab cba
Eine Funktion, die aus einer gegebenen Permutation die in lexikographischer Ordnung nächst folgende erzeugt, kann wie folgt implementiert werden:
def next_permutation(a): i = len(a) -1 #letztes Element; man arbeitet sich von hinten nach vorne durch while True: # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird if i <= 0: return False # a ist letzte Permutation i -= 1 if a[i]<a[i+1]: break #lexikogr. Nachfolger hat größeres a[i] j = len(a) while True: j -= 1 if a[i] < a[j]: break a[i], a[j] = a[j], a[i] #swap a[i], a[j] #sortiere aufsteigend zwischen a[i] und Ende #zur Zeit absteigend sortiert => invertieren i += 1 j = len(a) -1 while i < j: a[i], a[j] = a[j], a[i] i += 1 j-= 1 return True # eine weitere Permutation gefunden def naiveTSP(graph): start = 0 result = range(len(graph))+[start] rest = range(1,len(graph)) c = pathCost(result, graph) while next_permutation(rest): r = [start]+rest+[start] cc = pathCost(r, graph) if cc < c: c = cc result = r return c, result
Komplexität: Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also
- Beispiel
| i = 0 | j = 3 | |||
| ↓ | ↓ | |||
| 1 | 4 | 3 | 2 | #input für next_permutation |
| i = 2 | j = 3 | |||
| ↓ | ↓ | |||
| 2 | 4 | 3 | 1 | # vertauschen der beiden Elemente |
| i = 2 | ||||
| j = 2 | ||||
| ↓ |
| |||
| 2 | 1 | 3 | 4 | #absteigend sortiert |
Stirling'sche Formel
Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Stirling'sche Formel z.T. starke Vereinfachungen erzielen.
Erfüllbarkeitsproblem
geg.:
- n Boolsche Variablen und deren Negation
- Logischer Ausdruck in
- zB ...
Grammatik eines logischen Ausdrucks(in BNF): <EXP> ::= <DISJ> <DISJ> ::= <CONJ> | <DISJ> <CONJ> <CONJ> ::= <TERM> | <CONJ> <TERM> <TERM> ::= ( <EXPR> ) | ¬( <EXPR> ) | <VAR> | ¬<VAR> <VAR> ::= | ... |
ges.: Eine Belegung der , so dass der gegebene Ausdruck "True" wird
Naive Lösung
Probiere alle Bedingungen aus Komplexität
Im Allgemeinen ist das der effizienteste bekannte Algorithmus
Normalformen von logischen Ausdrücken
k-Konjunktionen-Normalform(k-CNF)
- ein "Literal" ist eine Variable oder deren Negation
- jeweils k Literale werden mit in einer Disjunktion verknüpft
- Disjunktionen werden mit in einer Konjunktion verbunden
Grammatik eines Ausdrucks in k-CNF(wieder in BNF): <EXP> ::= <CONJ> <CONJ> ::= <DISJ> | <CONJ> <DISJ> <DISJ> ::= ( <LIT> ... <LIT> ) <!-- k Literale --> <LIT> ::= <VAR> | <VAR> <VAR> ::= | ... |
Beispiele:
- 3-CNF:
- 2-CNF: ...
Satz:
- Jeder logische Ausdruck kann in polynomieller Zeit in 3-CNF umgewandelt werden
- Im Allgemeinen kann ein logischer Ausdruck nicht in 2-CNF umgeschrieben werden
Implikationen-Normalform(INF)
Konjunktionen von Implikationen:
- zB
Grammatik eines Ausdrucks in INF(you know the drill ;)): <EXP> ::= <CONJ> <CONJ> ::= <IMPL> | <CONJ> <IMPL> <IMPL> ::= ( <LIT> <LIT> ) <LIT> ::= <VAR> | <VAR> <VAR> ::= | ... |
Satz:
- jeder Ausdruck in 2-CNF kann in INF umgewandelt werden (siehe z.B. hier):
Beachten Sie, dass beide Implikationen in die Normalform eingefügt werden müssen, um die Symmetrie des Problems zu erhalten. Aus wird also .
Außerdem kann jeder Ausdruck in INF als gerichteter Graph dargestellt werden
- Jede Variable und ihre Negation sind jeweils 1 Knoten (d.h. 2n Knoten insgesamt).
- Jede Implikation ist eine gerichtete Kante.
Stark zusammenhängende Komponenten
geg.: gerichteter Graph
1. Bestimme die post Order Time (mit Tiefensuche) 2. Transponieren des Graphen 3. Bestimme ConnComp mit bekannten CC Algorithmen, aber so, dass Knoten in absteigender post Order behandelt werden
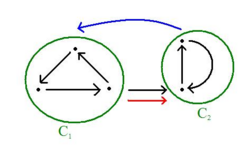
Beweis: 1.Bilde Komponentengraphen:
Knoten: jede SCC ist ein Knoten Kanten: mit und
*Eigenschaft 1: der Komponentengraph ist :azyklisch:
*Eigenschaft 2: falls dann
(ausserdem gilt: es gibt keinen Weg )
aber: in transponierten Graphen sind alle Kanten umgedreht
*Eigenschaft 3: falls , dann gilt
Eigenschaft 2-3 im transponierten Graphen gibt es nie einen Pfad
Falls
Schritt 3 des Algorithmus kann von einem geg. Startknoten nur die Knoten derselben SCC erreichen
q.e.d.
postOrderTime
## In einem Baum: besuche erst die Kinder, dann die Wurzel
def postOrderTime(graph):
visited = [None] * len(graph)
def visit(node, count):
#markiert, dass 'node' besucht wurde, aber noch nicht fertig ist
visited[node] = -1
for neighbor in graph[node]:
if visited[neighbor] is not None: continue
count = visit(neighbor, count)
visited[node] = count
count += 1
return count
count = 0
for node in range(len(graph)):
if visited[node] is not None: continue
count = visit(node, count)
return visited
transpose
## Kehre die Richtung der Pfeile in einem Graphen um (tut nichts fuer ungerichtete Pfeile und Graphen).
def transpose(graph):
grapht = [[] for k in range(len(graph))]
for node in range(len(graph)):
for neighbor in graph[node]:
grapht[neighbor].append(node)
return grapht
strongCC
## Jede Komponente durch e. Ankerknoten repräsentiert
## Jedes SCC ist die Menge aller Knoten mit identischem Ankterknoten
def strongCC(graph):
# Prinzip: Tiefensuche mit absteigender Post-Order-Time
postOrder = postOrderTime(graph)
# ordered = [(knotenindex, POT), ...]
ordered = zip(range(len(graph)), postOrder)
ordered.sort(key=lambda x: x[1], reverse=True)
grapht = transpose(graph)
anchors = [None] * len(graph)
def visit(node, anchor):
if anchors[node] is not None: return
anchors[node] = anchor
for neighbor in grapht[node]:
visit(neighbor, anchor)
for node in ordered:
visit(node[0], node[0])
return anchors
Anwendung auf 2-SAT Problem
geg.: Implikationen-Normalform, dargestellt als gerichteter Graph.
Eigenschaft: alle Variablen in derselben SCC müssen den gleichen Wert haben, weil
dürfen nie in derselben SCC sein, weil ein Widerspruch ist
Algorithmus für Erfüllbarkeit von INF: teste diese Eigenschaft für jede stark zusammenhängende Komponente des Implikationengraphen
Das funktioniert leider nicht für k-SAT mit
Wichtige Algorithmen, die in der Vorlesung nicht behandelt werden
- Max Flow (zur Bestimmung des maximalen Flusses durch ein Netzwerk, z.B. bei Ölpipelines)
- Matching (auch Paarung genannt): Teilmenge der Kanten eines Graphen, wobei keine zwei Kanten einen gleichen Knoten besitzen
- Anwendungsbereiche: Zuordnung von Gruppen, z.B. Arbeitsamt (Zuordnung Arbeitssuchender - Stellenangebot), Universität (Zuordnung Studenten - Übungsgruppen)




































![{\displaystyle a<b\Leftrightarrow {\begin{cases}n<m&{\text{ falls fuer }}0\leq i\leq k-1{\text{ gilt: }}a[i]=b[i]\\a[j]<b[j]&{\text{ falls fuer }}0\leq i\leq j-1{\text{ gilt: }}a[i]=b[i],{\text{ aber fuer ein }}j<k:a[j]\neq b[j]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994a444737516ade2f1e806cafa2393459a1004e)







































