Iteration versus Rekursion

Rekursion in der Informatik:

Einen Funktion f ist rekursiv wenn sie sich selbst aufruft. Die Funktion heißt indirekt-rekursiv wenn sie sich selbst aufruft über den Umweg einer anderen Funktion (oder mehrerer anderer Funktionen).

Beispiel einer indirekten Rekursion:

   foo  --->  bar  --->  foo
      ruft auf    ruft auf

Entscheidende Eigenschaften der Rekursion

• Jeder Aufruf einer rekursiven Funktion f hat sein eigenes Set von lokalen Variablen, d.h. der rekursive Aufruf hat die gleichen Anweisungen auszuführen, aber er hat seine eigenen Daten. Betrachten wir z.B. die rekursive Funktion

     def f(n):
         r = f(n-1)
         ... # weiterer Code
         return r

Für ein gegebenes n erhalten wir die Aufrufkette:

     f(n)             1.Ebene
        f(n-1)        2.Ebene
             f(n-2)   3.Ebene
                      ...

Die Funktionsaufrufe der verschiedenen Ebenen werden so ausgeführt, als ob wir für jede Ebene eine eigene Funktion f₁(n₁), f₂(n₂), f₃(n₃) usw. definiert hätten:

     f1(n1)            1.Ebene ---> n1 = n
         f2(n2)        2.Ebene ---> n2 = n1-1
             f3(n3)    3.Ebene ---> n3 = n2-1 = n1-2 = n-2
                       ...

Die Funktionen f₁(n₁), f₂(n₂), f₃(n₃) enthalten alle den gleichen Code, aber mit unterschiedlich benannten Variablen n₁, n₂, n₃. Durch diese Umbenennungen sollte die obige Aussage deutlich werden.

• Jede rekursive Funktion muß mindestens einen nicht-rekursiven Zweig haben. Dieser Zweig wird als Basisfall oder Rekursionsabschluss bezeichnet.

• Jeder rekursive Aufruf muß über endlich viele Stufen auf einen Basisfall zurückgeführt werden, denn sonst erhält man eine Endlosrekursion (und das ist fast so übel wie eine Endlosschleife -- "fast" deshalb, weil die Endlosrekursion spätestens dann abbricht wenn der Speicher voll ist --> siehe Übung 7 Aufgabe 1).

• Die Anzahl der rekursiven Aufrufe bis zum Rekursionsabschluss bezeichnet man als Rekursionstiefe d.

• Jede rekursive Funktion kann in eine iterative Funktion umgewandelt werden, die statt rekursiver Aufrufe eine Schleife enthält. Wir beschreiben dies unten anhand von Beispielen.

Arten der Rekursion

Die Arten der Rekursion sind hier nicht vollständig angegeben, es gibt noch weitere. Aber die hier folgenden sind für die Programmierung am wichtigsten.

Lineare Rekursion

• Jeder Ausführungspfad durch die Funktion f enthält höchstens einen rekursiven Aufruf.
• Höchstens einen, weil mindestens ein Pfad existieren muss, der keinen rekursiven Aufruf enthält (der Basisfall).

⇒ Das Ergebnis der Aufrufe ist eine 1-dimensionale "Rekursionskette".

Baumrekursion

(auch Kaskadenrekursion)

• Mindestens ein Ausführungspfad durch die Funktion enthält mindestens 2 rekursive Aufrufe.
• Baumrekursion ist damit das Gegenteil der linearen Rekursion.

⇒ Das Ergebnis der Aufrufe ist ein verzweigter "Rekursionsbaum". Ein baum-rekursiver Algorithmus ist deshalb häufig ineffizient: Wird der Pfad mit mehreren rekursiven Aufrufen mindestens Ω(d)-mal ausgeführt (wobei d die Rekursionstiefe) ist, entsteht ein Rekursionsbaum mit O(2^d) Knoten, also ein Algorithmus mit exponentieller Komplexität.

Course-of-values recursion

• Das Ergebnis des rekursiven Aufrufes für Argument n hängt nur von den Ergebnissen der letzten p-Aufrufe, also für Argument n-1,n-2,...,n-p ab (wobei p eine Konstante ist).

Primitive Rekursion

• Spezialfall der course-of-values recursion mit p=1.

⇒ Das ist auch ein Spezialfall der linearen Rekursion, denn wenn das Ergebnis nur von einem rekursiven Aufruf abhängt, kann kein Rekursionsbaum entstehen.

Endrekursion

• In jedem rekursiven Ausführungspfad ist der rekursive Aufruf der letzte Befehl vor dem return-Befehl.

⇒ Das ist ein Spezialfall der linearen Rekursion, denn es kann nur einen letzten Befehl vor jedem return geben, ein zweiter rekursiver Aufruf könnte allenfalls der vorletzte Befehl sein.

Beispiele und Umwandlung in Iteration

Beispiel für alle Rekursionsarten: Fibonacci-Zahlen

Wir verdeutlichen die verschiedenen Rekursionsarten und ihre Umwandlung in iterative Algorithmen am Beispiel der Fibonacci-Zahlen.

Fibonacci-Zahlen

Die n-te Fibonacci-Zahl ist gemäß der folgenden Rekursionsformel definiert.

f₀=0

f₁=1

f_n=f_n-1+f_n-2

Es ergibt sich die Folge:

f_k=0, 1, 1, 2, 3, 5, 8, 13,....., (⇒ Die Reihe wächst exponentiell an.)

Im folgenden zeigen wir 5 verschiedene Algorithmen zu Berechnung der n-ten Fibonacci-Zahl:

Version 1: Naive rekursive Implementation

Implementiert man einfach die rekursive Formel der Definition, erhält man:

def fib1(n):                      # Funtion berechnet die n-te Fibonacci-Zahl
    if n <= 1: 
         return n                 # Rekursionsabschluss
    return fib1(n-1) + fib1(n-2)  # Baumrekursion

Die Funktion fib1(n) ist ein Beispiel für eine Baumrekursion mit exponentieller Komplexität. Der Aufrufbaum sieht dann wie folgt aus:

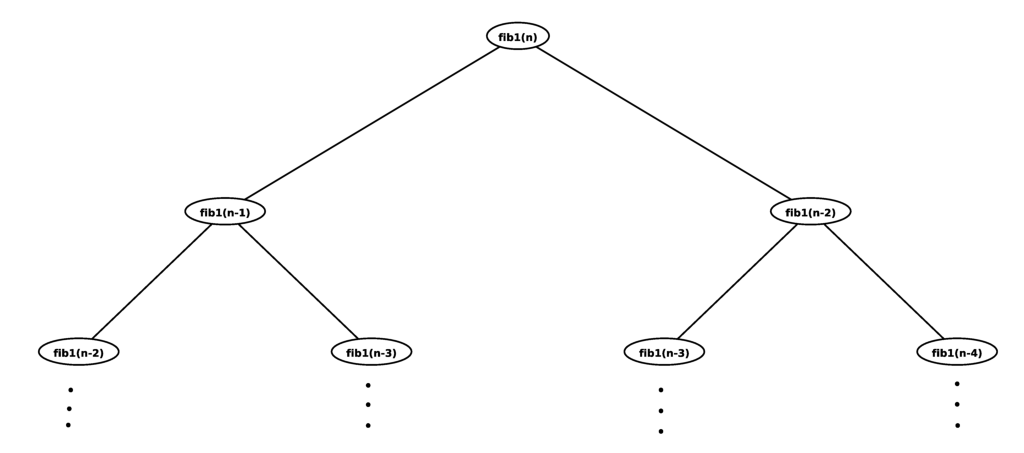
Im Falle der Fibonacci-Zahlen ist dies ein ungünstiger Algorithmus, weil viele Teilergebnise wiederholt berechnet werden (z.B. f_n-2 und f_n-3). Aber einige Probleme sind echt Baumrekursiv, z.B. das Ausrechnen der möglichen Züge beim Schachspiel.

Es gilt folgender grundlegender Satz

Jeder rekursiver Algorithmus kann mit Hilfe eines Stacks in einen iterativen Algorithmus umgewandelt werden (d.h. mit einer Schleife statt einer Rekursion). Das bedeutet, dass rekursive Programme gleichmächtig sind wie Programme mit Schleifen (z.B. WHILE-Programme, siehe erste Vorlesung), d.h. gleichmächtig wie die Turing-Maschine. Die Komplexität des Algorithmus ändert sich durch die Umwandlung nicht.

Version 2: Umwandlung in einen iterativen Algorithmus mit Stack

def fib2(n):
    stack = [n]   # der Stack enthält als erstes Teilproblem das ursprüngliche Problem "n-te Fibonacci-Zahl berechnen"
    f = 0         # f wird später die Lösung enthalten
    
    while len(stack) > 0:          # solange noch was auf dem Stack liegt, ist noch Arbeit zu tun
          k = stack.pop()          # Teilproblem von Stack entnehmen und lösen
          if k <= 1:               
               f += k              # entweder: Teilergebnis zur Lösung addieren (das war vorher der Rekursionsabschluss)
          else:                    
               stack.append(k-1)   # oder: zwei neue Teilprobleme auf dem Stack ablegen 
               stack.append(k-2)   # (das waren vorher die rekursiven Aufrufe)
    return f

Version 3: Course-of-values recursion

Wie man unmittelbar aus der Definitione erkennt, ist die Berechnung der Fibonacci-Zahlen Course-of-values rekursiv mit p=2. Eine entsprechende Implementation verwendet eine Hilfsunfktion, die immer die Ergebnisse der p letzten Aufrufe zurückgibt:

def fib3(n):
    if n == 0: return 0     # Rekursionsabschluss
    f1,f2 = fib3Impl(n)     # Hilfsfuntion, f1 ist die Fibonacci-Zahl von n und f2 ist dei Fibonacci-Zahl von (n-1)
    return f1

Die Hilfsfunktion enthält jetzt die eigentliche Rekursion. Sie berechnet die Fibonacci-Zahlen f_k und f_k-1 aus den Zahlen f_k-1 und f_k-2:

def fib3Impl(n):
    if n == 1: return 1, 0         # gebe die Fibonacci-Zahl von 1 und die davor zurück
    else:                          # rekursiver Aufruf
       f1,f2 = fib3Impl(n-1)       # f1 ist Fibonacci-Zahl von (n-1), f2 die von (n-2)
       return f1 + f2, f1          # gebe neue Fibonacci-Zahl fn=f1+f2 und die vorherige (fn-1=f1) zurück.

⇒ Diese Implementation ist jetzt linear-rekursiv (aber nicht endrekursiv). Sie hat damit lineare Komplexität und nicht exponentielle wie die beiden vorherigen Versionen.

Es gilt folgender Satz

Jede Course-of-values Rekursion kann in Endrekursion umgewandelt werden.

Version 4: Endrekursiv

Man gelangt von der Course-of-values recursion zur Endrekursion, indem man einfach die Berechnungsreihenfolge umkehrt: statt rückwärts von f_n nach f₀ zu arbeiten, arbeitet man vorwärts von f₀ nach f_n. Dazu muss der Hilfsfunktion eine Zählvariable übergeben werden, die angibt, wie viele Schritte noch bis zum Ziel f_n verbleiben. Außerdem erhält die Hilfsfunktion die beiden vorherigen Fibonacci-Zahlen als Argument übergeben:

def fib4(n)
    if n == 0: 
       return 0    
    else:                    
       return fib4Impl(0, 1, n) 

Die Hilfsfunktion:

def fib4Impl(f1, f2, counter)
    if counter == 1: 
       return f2
    else:
       return fib4Impl(f2, f1+f2, counter-1)   # f2 ist die vorletzte Fibonacci-Zahl,
                                               # f1+f2 wird die neue Fibonacci-Zahl und wir müssen counter um 1 herunterzählen

Beispiel mit n=3:

	f1	f2	counter
fib4Impl 1.Aufruf	0	1	3
fib4Impl 2.Aufruf	1	1	2
fib4Impl 3.Aufruf	1	2	1 ⇒ Rekursionsabschluss ⇒ return 2

⇒ Ergebnis von fib4(3) (die 3. Fibonacci-Zahl) ist 2.

Es gilt folgender grundlegender Satz

Jede endrekursive Funktion kann ohne Stack in eine iterative Funktion umgewandelt werden.

Bei einigen Programmiersprachen (z.B. Lisp, Scheme) wird dies von Compiler sogar automatisch erledigt (als Programmoptimierung, weil Iteration im allgemeinen schneller ist als Rekursion).

Version 5: Umwandlung in einen iterativen Algorithmus ohne Stack

def fib5(n):
    f1, f2 = 0, 1
    while n > 0:
        f1, f2 = f2, f1+f2
        n -= 1
    return f1

Das ist genau das gleiche wie fib4Impl. Aber anstelle eines rekursiven Aufrufes werden einfach die Variablen f₁ und f₂ wiederverwendet (mit den neuen Werten überschrieben). Dies ist möglich, weil die originalen Werte nicht mehr benötigt werden, denn der rekursive Aufruf bei fib4Impl war der letzte Befehl vor dem return (Endrekursion!).

Beispiel für die Umwandlung von Rekursion in Iteration: treeSort

Input:

• ein balancierter Binärbaum, repräsentiert durch seinen Wurzelknoten root
• ein leeres dynamisches Array a, das später die sortierten Elemente des Baums enthalten wird

Aufgerufen wird:

    treeSort(root,a)  # kopiert Elemente des Baums sortiert in Array a

Wiederholung des rekursiven Algorithmus (vergleiche Abschnitt "Sortieren mit Hilfe eines selbst-balancierenden Suchbaums"):

def treeSort(node,a):
   if node is None: 
       return
   treeSort(node.left,a)
   a.append(node.key)
   treeSort(node.right,a)

Dieser Algorithmus ist baumrekursiv, was nicht weiter überrascht, denn die Rekursion dient ja zur Traversierung eines Baumes. In diesem Fall führt Baumrekursion nicht zu exponentieller Komplexität, weil die Tiefe des Baum nur O(log N) ist. Dadurch benötigt treeSort nur O(2^{log N}) = O(N) Schritte zum Auslesen des Baumes (das Füllen das Baumes benötigt allerdings O(N log N) Schritte und dominiert den Algorithmus).

Die Implementation als iterative Funktion erfolgt mit Hilfe eines Stacks und einer Hilfsfunktion traverseLeft, die den Stack füllt:

def treeSortIterative(root, a):
   stack = []
   traverseLeft(root, stack)   # fülle Stack mit den Knoten des linken Teilbaums von root
   while len(stack) > 0:
       node = stack.pop()
       a.append(node.key)
       traverseLeft(node.right, stack)  # fülle Stack mit den Knoten des linken Teilbaums von node.right

Hilfsfunktion:

def traverseLeft(node, stack):
   while node is not None:
       stack.append(node)
       node = node.left

Auflösung rekursiver Gleichungen

Um die Komplexität eines rekursiven Algorithmus zu berechen, müssen wir die notwendige Schrittzahl für ein Problem der Größe N bestimmen. Die Schrittzahl einer rekursiven Funktion setzt sich zusammen aus den Schritten, die in der Funktion selbst ausgeführt werden, sowie denen, die die verschiednenen rekursiven Aufrufe beitragen. Um dies allgemein auszudrücken, nehmen wir an, dass jeder rekursive Aufruf sich auf ein Teilproblem des originalen Problems bezieht. Die Größe des i-ten Teilproblems sei n/b_i (wenn wir also auf dem Originalproblem weiterarbeiten, gilt b_i=1), und es soll a_i Teilprobleme dieser Größe geben. Dann wird die gesuchte Schrittzahl durch folgende Formel ausgedrückt:

<math>\underbrace{T(n)}_{\mbox{Schrittzahl}} = \underbrace{ a_1T\left(\frac{n}{b_1}\right)+a_2T\left(\frac{n}{b_2}\right)+\cdots+a_kT\left(\frac{n}{b_k}\right) }_{\mbox{rekursive Teilprobleme}}

+\underbrace{f(n)}_{\mbox{nicht-rekursiver Teil}}</math>

Bemerkung: Im allgemeinen arbeiten die rekursiven Aufrufe auf Teilproblemen ganzzahliger Größe. Daher muss man <math>\frac{n}{b_i}</math> gegebenenfalls aufrunden <math>\left\lceil\frac{n}{b_i}\right\rceil</math> oder abrunden <math>\left\lfloor\frac{n}{b_i}\right\rfloor</math>. Diese Rundungen spielen für die Auflösung der Formeln meist keine Rolle, weil die Rundungsfehler für große n vernachlässigbar sind.

Rekursionsformeln dieses Typs haben wir z.B. im Kapitel Sortieren bereits behandelt. Hier wollen wir allgemeine Strategien angeben, wie man die rekursive Form dieser Formeln in eine explizite Form (die keine Ausdrücke der Art <math>T\left(\frac{n}{b_i}\right)</math> mehr enthält) überführt .

Master-Theorem

Im Speziallfall k=1 (d.h. alle Unterprobleme haben die gleiche Größe) vereinfacht sich obige Formel zu:

<math>T(n) = a\,T\left(\frac{n}{b}\right)+f(n)</math>

Hier gibt es mit dem Master-Theorem eine sehr allgemeine Regel, wie man dies in eine explizite Form bringt. Einen Beweis für das Master-Theorem findet man z.B. bei T. Cormen, C. Leiserson, R.Rivest: "Algorithmen - eine Einführung".

Wir definieren zunächst den Rekursionsexponenten:

<math>\rho=\log_b (a)</math>

Ja nach dem Verhalten des nicht-rekursiven Anteils unterscheiden wir 3 Fälle

Fall 1:

Falls die Funktion f(n) sehr effizient ist, so dass für ihre Komplexität gilt

<math>f(n) \in O(n^{\rho-\epsilon}) , \epsilon>0</math>

In diesem Fall dominieren die Kosten der Rekursion, und die Komplexität der rekursiven Funktion ergibt sich aus dem Rekursionsexponenten

<math>T(n) =\Theta(n^{\rho})</math>

Fall 2:

Wenn die Funktion f(n) genauso effizient ist wie die Rekursion, wenn also gilt

<math>f(n) \in \Theta(n^{\rho}) </math>

dann addieren sich die Kosten für f(n) und für die Rekursion, und wir erhalten:

<math>T(n) =\Theta(n^{\rho}\cdot\log n)</math>

Fall 3:

Wenn die Funktion f(n) nicht sehr effizient ist, so dass für ihre Komplexität gilt

<math>f(n) \in \Omega(n^{\rho+\epsilon})</math>

kann das Master-Theorem nur dann eine Aussage machen, wenn außerdem gilt

<math>a\,f\left(\frac{n}{b}\right)\le c\,f(n)\,\textrm{mit}\,c<1</math>

Jetzt dominieren die Kosten von f(n), und die Komplexität wird

<math>T(n) =\Theta(f(n))</math>

Beispiel: Merge Sort

Im Falle von Merge Sort wird das Problem in zwei gleiche Teile zerlegt, die beide rekursiv sortiert werden (es gilt also a=2, b=2). Das Zusammenfügen der beiden Teile erfordert Θ(n) Vergleiche. Wir erhalten also die Formel

<math>T(n) = \underbrace{ 2\,T\left(\frac{n}{2}\right)}_{\mbox{rekursive Aufrufe von MergeSort}}+\underbrace {\Theta(n)}_{\textrm{Merge}}</math>

Für den Rekursionsexponenten erhalten wir

<math>\rho=log_2 2 = 1</math>

Mit f(n) ∈ Θ(n) = Θ(n^ρ) trifft Fall 2 zu, und wir erhalten für die Komplexität von MergeSort das bereits bekannte Ergebnis:

<math>T(n) \in \Theta(n^ \rho \log n) = \Theta(n\,\log n)</math>

Fälle die nicht durch das Master-Theorem abgedeckt sind:

• wenn <math>k \ > 1</math>: rekursive Teilprobleme verschiedener Grösse
• wenn <math>f(n) \in O\left(\frac{n^\rho}{\log n}\right)</math>: Die Komplexität von f(n) liegt genau zwischen den Fällen 1 und 2.
• wenn <math>f(n) \in \Omega\left(n^\rho \log n\right)</math>: Die Komplexität von f(n) liegt genau zwischen den Fällen 2 und 3.
• wenn für alle c<1 gilt <math>a\,f\left(\frac{n}{b}\right)> c\,f(n)</math>: Die Komplexität der Funktion f(n) auf den reduzierten Problemen ist zu groß.

Rekursionsbäume und Substitutionsmethode

Wenn das Master-Theorem nicht anwendbar ist, muss man die Rekursionsformel selbst auflösen. Dies gilt zum Beispiel, wenn der Algorithmus das Problem in zwei ungleich große Teile zerlegt. Wir betrachten das folgende Beispiel, bei dem das Problem in Teile der Größe 1/3 und 2/3 zerlegt wird und das Zusammenfügen der Teile c*n Schritte erfordert:

<math>T(n) = \underbrace{ T\left(\frac{n}{3}\right)}_{\frac{1}{3}\mbox{ der Daten}}+\underbrace {T\left(\frac{2n}{3}\right)}_{\frac{2}{3}\mbox{ der Daten}} +\underbrace {c\cdot n}_{\mbox{Zusammenfügen}}</math>

Wir bilden zuerst den Rekursionsbaum dieses Problems, wobei für jeden Knoten die Größe des Teilproblems angegeben ist, das dieser Knoeten lösen muss:

                                                n    
                                              /    \
                                             /      \
                                            /        \
                                           /          \
                                          /            \
                                      (n/3)            (2n/3)
                                    /       \          /     \
                                   /         \        /       \
                                  /           \      /         \
                               (n/9)       (2n/9)  (2n/9)      (4n/9)

Jeder Knoten ruft rekursiv seine Kindknoten auf und fügt dann deren Teilprobleme zusammen. Wir berechnen den Aufwand, den allein das Zusammenfügen auf jeder Ebene des Baumes verursacht. Auf der obersten Ebene (Ebene 1) gibt es nur ein Teilproblem, und der Aufwand ist c*n. Auf Ebene 2 haben wir zwei Teilprobleme mit Aufwand

<math>c\,\frac{n}{3}</math> und <math>c\,\frac{2\,n}{3}</math>

Der Gesamtaufwand für das Zusammenfügen auf Ebene 2 ist die Summe dieser Ausdrücke, wir erhalten also wieder c*n. Für Ebene 3 gilt wiederum

<math>c\left(\frac{n}{9}+\frac{2\,n}{9}+\frac{2\,n}{9}+\frac{4\,n}{9}\right)=c\,n</math>

Offensichtlich gilt also für alle Ebenen, dass das Zusammenfügen der Teilprobleme insgesamt c*n Schritte erfordert. Zur Berechnung des Gesamtaufwands müssen wir nun noch die Anzahl der Ebenen, also die Tiefe d des Baumes, schätzen. Die Rekursion muss spätestens dann enden, wenn ein Teilproblem der Größe 1 erriecht wird, weil dies nicht weiter zerlegt werden kann. Die Rekursion endet also, wenn

<math>\left(\frac{2}{3}\right)^d n=1</math>.

Auflösen dieser Formel nach d ergibt

<math>d=\log_\frac{3}{2}(n)</math>

Wir leiten daraus die Vermutung ab, dass für die Komplexität unseres Algorithmus gilt

<math>T(n) \in O\left(\log_\frac{3}{2}(n)\cdot c\cdot n\right)</math>

Nach den Regeln der O-Notation vereinfacht sich dies aber zu

<math>T(n) \in O\left(n\,\log n\right)</math>

Diese Vermutung muss aber noch formal bewiesen werden (der Rekursionsbaum reicht als Beweis nicht aus). Der Beweis erfolgt durch die Substitutionsmethode. Das bedeutet, dass wir unsere Vermutung auf der rechten Seite der Rekursionsformel einsetzen und beweisen, dass eine wahre Aussage herauskommt. Für hinreichend große n und hinreichend großes d kann die Vermutung geschrieben werden als

<math>T(n) \le d\,n\,\mbox{ld}(n) </math>

(wir haben hier willkürlich Logarithmen zu Basis 2 eingesetzt -- die Basis in der O-Notation ist bekanntlich beliebig). Einsetzen in die Rekursionsformel liefert

<math>T(n) \le T\left(\frac{n}{3}\right)+ T\left(\frac{2n}{3}\right)+ c\,n \le d\,\frac{n}{3}\,\mbox{ld}\left(\frac{n}{3}\right)+ d\,\frac{2n}{3}\,\mbox{ld}\left(\frac{2n}{3}\right)+ c\,n</math>

Durch Ausmultiplizieren der Klammern und Trennen der Logarithmen von Quotionten in Differenzen von Logarithmen erhalten wir

<math> T(n) \le d\frac{1}{3}\,n\,\mbox{ld}(n)-d\,\frac{1}{3}\,n\,\mbox{ld}(3)+d\,\frac{2}{3}\,n\,\mbox{ld}(n)+d\,\frac{2}{3}\,n\,\mbox{ld}(2)-d\,\frac{2}{3}\,n\,\mbox{ld}(3)+c\,n</math>

Unter Beachtung von ld(2)=1 können wir die Terme wie folgt zusammenfassen

<math> T(n) \le d\,n\,\mbox{ld}(n)-d\,n\left(\mbox{ld}(3)-\frac{2}{3}\right)+c\,n</math>

Falls unsere Vermutung richtig ist, muss die rechte Seite kleiner oder gleich <math>d\,n\,\mbox{ld}(n) </math> sein. Um dies zeigen zu können, setzen wir

<math> d \ge \frac{c}{\mbox{ld}(3)-\frac{2}{3}}\, \Leftrightarrow\, d\left(\mbox{ld}(3)-\frac{2}{3}\right) \ge c</math>

(nach den Regeln der O-Notation kann d beliebig gewählt werden, solange es hinreichend groß ist). Wenn wir die Konstante c mit Hilfe dieses Ausdrucks ersetzen, erhalten wir

<math> T(n) \le d\,n\,\mbox{ld}(n)-d\,n\left(\mbox{ld}(3)-\frac{2}{3}\right)+c\,n \le

d\,n\,\mbox{ld}(n)-d\,n\left(\mbox{ld}(3)-\frac{2}{3}\right)+d\left(\mbox{ld}(3)-\frac{2}{3}\right)n</math> Die beiden letzten Terme heben sich aber gerade weg, und es bleibt übrig:

<math> T(n) \le d\,n\,\mbox{ld}(n)</math>

und somit

<math>T(n) \in O\left(n\,\log n\right)</math>

w.z.b.w.

Allgemein gilt, dass eine ungleiche Aufteilung in Teilprobleme die Komplexität eines rekursiven Algorithmus nicht verschlechtert, falls das Teilungsverhältnis konstant bleibt, falls der nichtrekursive Aufwand f(n) auf jeder Ebene in O(n) ist. Das gilt aber nicht, wenn das Problem immer in ein Teilproblem konstanter Größe und den Rest geteilt wird. Dann gilt mit einer Konstante p

<math>T(n) = T(p) + T(n-p) + c\cdot n</math>

und das Teilungsverhältnis wird umso schlechter, je größer n wird. Dies ist gerade der ungünstige Fall bei Quicksort, und wir haben gesehen, dass sich die Komplexität hier auf O(n²) verschlechtert.