Suchen

Das Suchen ist eine grundlegende Operation in der Informatik. Viele Probleme in der Informatik können auf Suchaufgaben zurückgeführt werden.

Gemeint ist mit Suchen das Wiederauffinden eines Datensatzes aus einer Menge von früher gespeicherten Datensätzen, oder das Auffinden einer bestimmten Lösung in einem (potentiell großen) Suchraum möglicher Lösungen. Ein paar einleitende Worte zum Suchproblem findet man hier.

Überblick über verschiedene Suchmethoden

Um sich der Vielseitigkeit des Suchproblems bewusst zu werden, ist es sinnvoll, sich einen Überblick über verschiedene Suchmethoden zu verschaffen.

Hier sei auch auf einen bereits existierenden Wikipedia-Artikel zu Suchverfahren verwiesen.

Allen gemeinsam ist die grundlegende Aufgabe, ein Datenelement mit bestimmten Eigenschaften aus einer großen Menge von Datenelementen zu selektieren. Dies kann, natürlich ohne jeden Anspruch auf Vollständigkeit, nach einer der jetzt diskutierten Methoden geschehen:

Schlüsselsuche: meint das Suchen von Elementen mit bestimmtem Schlüssel; ein klassisches Beispiel wäre das Suchen in einem Wörterbuch, die Schlüssel entsprechen hier den Wörtern, die Datensätze wären die zu den Wörtern gehörigen Eintragungen.

Bereichssuche: Im Allgemeinen meint die Bereichssuche in n-Dimensionen die Selektion von Elementen mit Eigenschaften aus einem bestimmten n-dimensionalen Volumen. Im eindimensionalen Fall will man alle Elemente finden, deren Eigenschaft(en) in einem bestimmten Intervall liegen. Die Verallgemeinerung auf n-Dimensionen ist offensichtlich. Ein Beispiel für die Bereichssuche in einer 3D-Kugel wäre ein Handy mit Geolokalisierung, welches alle Restaurants in einem Umkreis von 500m findet. Lineare Ungleichungen werden graphisch durch Hyperebenen repräsentiert. In 2D sind diese Hyperebenen Geraden. Die Ungleichungen können dann den Lösungsraum in irgendeiner Form begrenzen.

Ähnlichkeitssuche: Finde Elemente, die gegebenen Eigenschaften möglichst ähnlich sind. Ein prominentes Beispiel ist Google (=Ähnlichkeit zwischen Suchbegriffen und Dokumenten) oder das Suchen des nächstengelegenen Restaurants (Ähnlichkeit zwischen eigener Position und Position des Restaurants). Ein wichtiger Spezialfall ist die nächste-nachbar Suche.

Graphensuche: Hier wäre beispielsweise das Problem optimaler Wege zu nennen (Navigationssuche). Dieser Punkt wird später im Verlauf der Vorlesung noch einmal aufgegriffen werden.

Im jetzt folgenden wird nur noch die Schlüsselsuche betrachtet werden.

Sequentielle Suche

Die sequentielle oder lineare Suche ist die einfachste Methode, einen Datensatz zu durchsuchen. Hierbei wird ein Array beispielsweise sequentiell von vorne nach hinten durchsucht. Ein prinzipieller Vorteil der Methode ist, dass auf der Eigenschaft der Datenelemente, nach denen das Array durchsucht wird, keine Ordnung im Sinne von > oder < definiert zu sein braucht, lediglich die Identität (==) muss feststellbar sein. Der folgende Python-Code zeigt, wie man sequentielle Suche einsetzen kann:

a = ... # array mit den zu durchsuchenden Elementen

foundIndex = sequentialSearch(a, key) 
# foundIndex == -1 wenn nichts gefunden, 0 <math>\leq </math> foundIndex < len(a) wenn key gefunden (erster Eintrag mit diesem Wert)

Wir verwenden hier die Konvention, dass der zugehörige Arrayindex zurückgegeben wird, falls ein Element mit dem Schlüssel key gefunden wird (falls es mehrere solche Elemente gibt, wird das erste zurückgegeben). Das Ergebnis -1 signalisiert hingegen, dass kein solches Element gefunden wurde. Die Funktion sequentialSearch kann folgendermaßen implementiert werden:

def sequentialSearch(a, key):
   for i in range(len(a)):
       if a[i] == key:  # bzw. allgemeiner a[i].key == key 
           return i
   return -1

Wir wollen jetzt die Komplexität dieses Algorithmus bestimmen, wobei die Problemgröße durch N = len(a) gegeben ist.

Dabei nimmt man an, dass der Vergleich in der inneren Schleife (a[i] == key) jeweils <math> \mathcal{O}(1)</math> ist (diese Annahme könnte verletzt sein, wenn der Vergleichsoperator eine komplizierte Berechnung mit höherer Komplexität ausführen muss). Bei einer erfolglosen Suche wird dieser Vergleich in der for-Schleife N-mal durchgeführt (<math> \mathcal{O}(N)</math>), bei einer erfolgreichen Suche im Mittel (N/2)-mal (ebenfalls <math> \mathcal{O}(N)</math>). Nach der Verschachtelungsregel erhält man also eine gesamte Komplexität von <math> \mathcal{O}(N)</math>.

Der Name lineare Suche rührt von diesem linearen Anwachsen der Komplexität mit der Arraygröße her.

Binäre Suche

Wie wir weiter unten zeigen werden, gestattet es diese Suchmethode, die Gesamtdauer der Suche in großen Datensätzen beträchtlich zu verringern. Die Methode beruht auf dem Divide and Conquer-Prinzip, wobei die Suche in jedem Schritt rekursiv auf eine Hälfte des Datensatzes eingeschränkt wird. Weitere Details zur Methode sind hier zu finden.

Die Methode ist nur dann anwendbar beziehungsweise effektiv, wenn folgendes gilt:

Auf der Eigenschaft der Daten, die zur Suche verwendet wird, ist eine Ordnung im Sinne von < oder > definiert.
Wir wollen uns auf Datensätze beschränken, die schon fertig aufgebaut sind, in die also keine neuen Elemente mehr eingefügt werden, wenn man mit dem Suchen beginnt. Ist dies nicht der Fall, müsste nach jeder Einfügung das Array neu sortiert werden (unter diesen Umständen wäre die Verwendung eines Suchbaumes geschickter).

Im unterschied zur sequenziellen Suche müssen wir jetzt das Array sortieren bevor die Suchfunktion aufgerufen werden kann:

a = [...,...]     # array
a.sort()   # sortiere über Ordnung des Schlüssels
foundIndex = binSearch(a, key, 0, len(a))  # (Array, Schlüssel, von wo bis wo suchen im Array)
# foundIndex == -1 wenn nichts gefunden, 0 <math>\leq</math>  foundIndex < len(a) wenn key gefunden (erster Eintrag mit diesem Wert)

Der folgende Algorithmus zeigt eine beispielhafte Implementierung der Methode:

def binSearch(a, key, start, end):  # start ist 1. Index, end ist letzter Index + 1
   size = end - start   # <math> \mathcal{O}(1)</math>
   if size <= 0:   # Bereich leer?  <math> \mathcal{O}(1)</math>
       return -1   # also nichts gefunden, <math> \mathcal{O}(1)</math>
   center = (start + end)/2   # Integer Division (d.h. Ergebnis wird abgerundet, wichtig für ganzzahlige Indizes) <math> \mathcal{O}(1)</math>
   if a[center] == key:  # <math> \mathcal{O}(1)</math>
       return center  # Schlüssel gefunden, <math> \mathcal{O}(1)</math>
   elif a[center] < key:  <math> \mathcal{O}(1)</math>
       return binSearch(a, key, center + 1, end)  # Rekursion in die rechte Teilliste
   else:
       return binSearch(a, key, start, center)  # Rekursion in die linke Teilliste

Zur Berechnung der Komplexität dieses Algorithmus vernachlässigen wir zunächst den Aufwand, den die Sortierung verursacht (wir diskutieren unten, wann dies nicht zulässig ist). Wir setzen N = len(a).

Im obigen Code ist zu erkennen, dass fast alle Anweisungen des Algorithmus die Komplexität <math>\mathcal{O}(1)</math>. Nach der Sequenzregel hat auch deren Hintereinanderausführung die Komplexität <math>\mathcal{O}(1)</math>. Es bleibt die Komplexität der Rekursion zu berechnen. Die gesamte Komplexität des Algorithmus (jetzt als Funktion f bezeichnet) setzt sich zusammen aus den oben erwähnten <math>\mathcal{O}(1)</math>-Anweisungen sowie der Rekursion auf einem Teilarray der halben Größe

<math>f(N) = \mathcal{O}(1) + f(N/2) = \mathcal{O}(1) + \mathcal{O}(1) + f(N/4) = ... = \underbrace{\mathcal{O}(1) + ... + \mathcal{O}(1) + \underbrace{f(0)}_{\mathcal{O}(1)\, \rightarrow \,\mathrm{size-Abfrage}}}_{n+1 \,\mathrm{Terme}} </math>

Zur Vereinfachung nehmen wir an <math> N = 2^n </math>, so dass gilt

<math> \rightarrow f(N) = \mathcal{O}(1) \cdot \mathcal{O}(n+1) = \mathcal{O}(n) = \mathcal{O}(\lg N) </math>

Für große Datenmengen ist die binäre Suche also weit effizienter als die lineare Suche. Verdoppelt sich beispielsweise die zu durchsuchende Datenmenge, so verdoppelt sich der Aufwand für die sequentielle Suche - bei der binären Suche hingegen benötigt man lediglich eine zusätzliche Vergleichsoperation.

Für kleine Daten (<math> N = 4,\, 5 </math>) ist die sequentielle Suche jedoch schneller als die binäre Suche, da hier die rekursiven Funktionsaufrufe teurer als das Mehr an Vergleichen sind. Ein anderer ungünstiger Fall ist gegeben, wenn nur sehr wenige Suchanfragen erfolgen (weniger als <math>\mathcal{O}(N)</math> viele). Dann wird der Aufwand durch das Sortieren des Arrays dominiert, ist also <math>\mathcal{O}(N \lg N) </math>. Auch dann ist sequentielle Suche vorzuziehen.

Eine relativ einfache Möglichkeit, die binäre Suche zu verbessern, ist die sogenannte Interpolationssuche. Hierbei wird die neue Position für die Suche, also die Mitte des Arrays, durch eine Schätzung ersetzt, die angibt, wo sich der Schlüssel innerhalb des Arrays befinden könnte. Bei der Suche in einem Telefonbuch nach dem Namen Zebra würde man ja auch nicht in der Mitte anfangen. Näheres hierzu im Buch von Sedgewick.

Um sich den Algorithmus der binären Suche klar zu machen, ist es instruktiv, sich die folgende Tabelle genauer anzusehen, die die sukzessive Belegung der Variablen bei verschiedenen Anfragen beschreibt. Die Testfälle wurden nach dem Prinzip des domain partitioning gewählt. Das zugehörige Array hat die Einträge

a = [2, 3, 4, 5, 6]

gesuchter key	start	end	size	center	return (-1 oder index)	Kommentare
4	0	5	5	2	2	gefunden
2	0	5	5	2		linker Randfall
	0	2	2	1
	0	1	1	0	0	gefunden
1	0	5	5	2		links außerhalb
	0	2	2	1
	0	1	1	0
	0	0	0		-1	nichts gefunden
6	0	5	5	2		rechter Randfall
	3	5	2	4	4	gefunden
5	0	5	5	2		typischer Fall
	3	5	2	4
	3	4	1	3	3	gefunden
7	0	5	5	2		rechts außerhalb
	3	5	2	4
	5	5	0		-1	nichts gefunden

Suchbäume

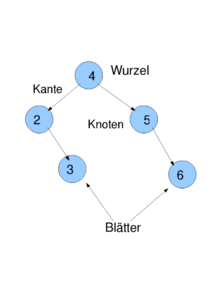
Effiziente Suchalgorithmen kann man elegent mit Hilfe von Binärbäumen realisieren. Eine kurze Einführung in Binärbäume findet man hier. Die Skizze erläutert wichtige Begriffe:

Bäume sind zweidimensional verkettete Strukturen. Sie gehören zu den fundamentalen Datenstrukturen in der Informatik. Da man in Bäumen nicht nur Daten speichern kann, sondern auch relevante Beziehungen der Daten untereinander, festgelegt über eine Ordnung auf der vergleichenden Dateneigenschaft (Schlüssel), eignen sich Bäume also insbesondere, um gesuchte Daten schnell wieder auffinden zu können.

Ein Binärbaum wie oben skizziert besteht aus einer Menge von Knoten, die untereinander durch Kanten verbunden sind. Jeder Knoten hat einen linken und einen rechten Unterbaum, der auch leer sein kann (in Python ließe sich dies mit None implementieren). Führt eine Kante von Knoten A zu Knoten B, so heißt A Vater von B und B Kind von A. Es gibt genau einen Knoten ohne Vater, den man Wurzel nennt. Knoten ohne Kinder heißen Blätter.

Ein Suchbaum hat zusätzlich die Eigenschaft, dass die Schlüssel jedes Knotens sortiert sind:

Suchbaumbedingung: Für jeden Knoten des Binärbaumes gilt: Alle Schlüssel im linken Unterbaum sind kleiner als der Schlüssel des gegebenen Knotens, alle Schlüssel im rechten Unterbaum sind größer. Wir wollen hierbei annehmen, dass jeder Schlüssel pro Datensatz nur einmal vorkommt, da sich sonst die >- oder <-Relation nicht mehr strikt erfüllen ließe.

Um die Verwendung eines Suchbaums zu motivieren, wollen wir von zwei Annahmen ausgehen:

Einfügen und Suchen im Baum wechseln sich ab. (Wenn das Suchen erst beginnt, nachdem alle Einfügungen erfolgt sind, wäre ein dynamisches Array mit binärer Suche wesentlich einfacher.)
Der Schlüssel, der die Anordnung bestimmt, kennt eine Ordnung (<-Relation oder >-Relation).

Zunächst definieren wir eine Knotenklasse für den Suchbaum:

class Node:
    def __init__(self, key):
        self.key = key
        self.left = self.right = None

Suche in einem Binärbaum

Wir nehmen nun an, dass der Baum durch eine Referenz auf den Wurzelknoten root gegeben ist. Dann kann man folgendermassen suchen:

root = ...    # Wurzel des Suchbaums
nodeFound = treeSearch(root, key)   # None, falls nichts gefunden

Hier verwenden wir die Konvention, dass der passende Knoten zurückgegeben wird, falls key gefunden wurde, oder None andernfalls. Die Suchfunktion wird rekursiv implementiert:

def treeSearch(node, key):
    if node is None:
        return None
    elif node.key == key: # gefunden
        return node       # => Knoten zurückgeben
    elif key < node.key:  # gesuchter Schlüssel ist kleiner
        return treeSearch(node.left, key)  # => im linken Unterbaum weitersuchen
    else:                 # andernfalls 
        return treeSearch(node.right, key) # => im rechten Unterbaum weitersuchen

Einfügen in einen Binärbaum

Bevor wir den Einfügealgorithmus implementieren, müssen wir festlegen, was passieren soll, wenn der einzufügende Schlüssel schon vorhanden ist. Mehrere Möglichkeiten bieten sich an:

Fehler signalisieren (exception auslösen)
nichts einfügen
nichts einfügen, aber einen boolean zurückgeben (false wenn nichts eingefügt wurde, true wenn etwas einfügt wurde)
nochmals einfügen (z.B. kann man die Klasse Node oben durch einen Zähler erweitern, der angibt, wie oft der betreffende Schlüssel bereits eingefügt wurde)

Die ersten 3 Punkte realisieren eine Mengensemantik, der letzte eine Multimenge. Wir entscheiden uns hier für Möglichkeit 2 (nichts einfügen). Das Prinzip des Einfügens besteht darin, im Baum dorthin abzusteigen, wo der Schlüssel sich befinden müsste (wie bei treeSearch), und dann an der betreffenden Stelle einen neuen Blattknoten zu erzeugen. Die Funktion gibt ein Knotenobjekt zurück, damit die Verkettungen im Elternknoten entsprechend angepasst werden können:

def treeInsert(node, key):
    if node is None:      # richtiger Platz gefunden
        return Node(key)  # => neuen Knoten einfügen
    if node.key == key:   # schon vorhanden
        return node       # => nicht tun
    elif key < node.key:     
        node.left = treeInsert(node.left, key) # im linken Teilbaum einfügen
    else:
        node.right = treeInsert(node.right, key) # im rechten Teilbaum einfügen
    return node

Ein Binärbaum wird aufgebaut, indem treeInsert für jeden Schlüssel aufgerufen wird. Wir verwenden hier ganze Zahlen als Schlüssel. Am Anfang ist der Baum leer:

root = None
root = treeInsert(root, 4)
root = treeInsert(root, 2)
root = treeInsert(root, 3)
root = treeInsert(root, 6)

Entfernen aus einem Binärbaum

Wir legen wiederum zuerst fest, was im Fehlerfall passieren soll, d.h. wenn der Schlüssel nicht vorhanden ist:

Auslösen einer Exception (KeyError)
nichts löschen
nichts löschen, aber ein boolean zurückgeben, das dies signalisiert.

Wir entscheiden uns wieder für Möglichkeit 2. Beim Entfernen eines Knotens unterscheiden wir nun 3 Fälle:

node, welcher key enthält, ist ein Blatt => kann einfach gelöscht werden
node hat nur linken Unterbaum oder nur rechten Unterbaum => durch Unterbaum ersetzen
node hat beide Unterbäume:
- Suche Vorgänger: <math>\max_{k < key} (k \in keys)</math> => ersetze node durch seinen Vorgänger und entferne Vorgänger. (Dies führt zu einem effizienten Algorithmus, weil der Vorgänger immer zu Fall 1 oder Fall 2 gehört. Wenn er nämlich einen rechten Unterbaum hätte, könnte er nicht der Vorgänger sein.)

Die Funktion, die den Vorgänger sucht, muss den größten Knoten im lnken Unterbaum suchen. Da diese Funktion nur in Fall 3 aufgerufen wird, gibt es den linken Unterbaum immer.

def treePredecessor(node):
    node = node.left
    while node.right is not None:
        node = node.right
    return node

Die oben angegebenen Fälle werden durch folgende Funktion realisiert:

def treeRemove(node, key):
    if node is None:   # key nicht vorhanden
        return node    # => nichts tun
    if key < node.key: 
        node.left = treeRemove(node.left, key)
    elif key > node.key:
        node.right = treeRemove(node.right, key)
    else:              # key gefunden
        if node.left is None and node.right is None:     # Fall 1
            node = None            
        elif node.left is None:     # Fall 2
            node = node.right       # +
        elif node.right is None:    # Fall 2
            node = node.left
        else:                       # Fall 3
            pred = treePredecessor(node)
            node.key = pred.key
            node.left = treeRemove(node.left, pred.key)
    return node

Komplexitätsanalyse

Um die Komplexität der Operationen auf einem Binärbaum zu bestimmen, müssen wir zunächst einige weitere Begriffe einführen:

Pfad

Ein Pfad zwischen zwei Knoten node₁ und node₂) ist eine Folge von Knoten node_k1,...,node_kn, so dass:

node_k1 == node₁
node_kn == node₂
node_ki und node_ki+1 haben eine gemeinsame Kante.

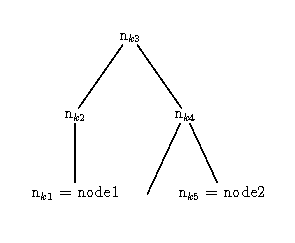Ein Baum ist definiert als ein Graph, in dem es zwischen beliebigen Knoten stets genau einen Pfad gibt.

Länge eines Pfades: Anzahl der Kanten im Pfad (= Anzahl der Knoten - 1)
Tiefe eines Knotens: Pfadlänge vom Knoten zur Wurzel des Baumes (die Wurzel hat also die Tiefe 0)
Tiefe des Baumes: maximale Tiefe eines Knotens

Allen Baumoperationen ist gemeinsam, dass sie entlang genau eines Pfades im Baum absteigen (welcher Pfad dies ist ergibt sich aus der Ordnung der Schlüssel). Der Abstieg endet, wenn entweder der gesuchte Schlüssel gefunden wird, oder wenn erkannt wird, dass der Schlüssel nicht vorhanden ist (wenn das Kind, wo der Schlüssel sein müsste, den Wert None hat). Während des Abstiegs werden in jedem Knoten nur Anweisungen ausgeführt, die konstante Zeit benötigen (1 Vergleich, wenn die Suche in dem Knoten erfolglos beendet wird, 2 Vergleiche, wenn der Schlüssel gefunden wird, und 3 Vergleiche, wenn im rechten oder linken Teilbaun weiter abgestiegen werden muss). Daraus folgt, dass die Suche im ungünstigsten Fall die Komplexität <math>\mathcal{O}(T)</math> hat, wobei T die Tiefe des Baumes (= längster Pfad, der durchlaufen werden kann) ist.

Ungünstigster Fall für die Baumoperationen

Um den ungünstigsten Fall für die Baumoperationen zu finden, müssen wir offensichtlich herausfinden, wie groß die Tiefe maximal werden kann. Es ist leicht zu erkennen, dass die Tiefe maximiert wird, wenn man sortierte Daten in den Baum einfügt:

Fügt man [1,2,3,4,5] in dieser Reihenfolge ein, muss man bei treeInsert stets in den rechten Teilbaum absteigen (weil der nächste Schlüssel immer größer als der größte bisherige Schlüssel ist) und dort ein rechtes Kind einfügen. Es ergibt sich folgender Baum:

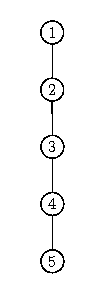
Dieser Baum hat die Tiefe 4. Die Funktion treeSerach verhält sich dann wie sequentielle Suche, man hat also durch die Verwendung des Suchbaums nichts gewonnen.

Allgemein gilt: Alle Operationen eine binären Suchbaums haben im ungünstigsten Fall die Komplexität <math>\mathcal{O}(N)</math>, wo N die Anzahl der Elemente im Baum bezeichnet. Eine offensichtliche Lösung der Problems besteht darin, die Elemente nicht in einer so ungünstigen Reihenfolge einzufügen (siehe Übungsaufgabe 5.1.c). Allerdings ist dies nicht immer möglich. Abhilfe schaffen dann selbst-balancierende Bäume.

Selbst-balancierende Suchbäume

Balance eines Suchbaumes

Um die Komplexität der Suchbaum-Operationen zu minimieren, müssen wir die Höhe des Baumes minimieren. Wir wollen also die Länge des längsten Pfades verkürzen, ohne dass ein anderer Pfad dadurch unnötig lang wird. Mit anderen Worten wollen wir erreichen, dass alle Pfade von der Wurzel zu den Blättern ungefährt die gleiche Länge haben. Diese Idee kann man formal durch den Begriff der Balance eines Suchbaums fassen. Um die Balance zu definieren, betrachten wir None als zusätzlichen Knoten, als sogenannten Sentinel (engl. für Wächter). Der sentinel-Knoten wird als rechter oder linker Nachfolger verlinkt, wenn der entsprechende Nachfolger nicht durch einen echten Knoten belegt ist:

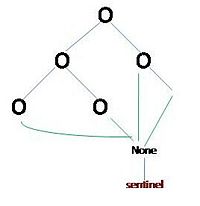
Wir definieren nun:

RS-Pfade

Pfad von root → sentinel. In jedem Binärbaum gibt es mehrere RS-Pfade.

Balance eines Baumes

Differenz zwischen der Länge des längsten und kürzesten RS-Pfads:

wobei <math>\{RS\}</math> die Menge aller RS-Pfade bezeichnet, und |P| die Länge des Pfades P.

vollständiger Baum

Balance <math>B=0</math>

Daraus folgt, dass alle Knoten (außer den Blättern) 2 Kinder haben müssen.

perfekt balancierter Baum

Balance <math>B \le 1</math>

alternative Definition für perfekt balancierte Bäume: Für jeden Knoten gilt, dass der rechte und linke Unterbaum ebenfalls perfekt balancierte Bäume sind und ihre Höhe sich höchstens um 1 unterscheidet. Leere Unterbäume sind per Definition perfekt balanciert und haben die Höhe Null.

Größe eines Baumes in Abhängigkeit von Balance und Tiefe

vollständiger Baum

Aus der Abbildung erkennt man, dass Ebene k eines vollständigen Baumes stets 2^k Knoten enthält (der grüne Knoten gehört nicht zum vollständigen Baum). Hat der Baum die Tiefe d, dann enthält er

N = 2⁰ + 2¹.....+ 2^d = 2^d+1 - 1

Knoten (und damit ebensoviele Datenelemente).

perfekt balancierter Baum

Für eine gegebene Tiefe d kann kein Baum mehr Elemente enthalten als der entsprechende vollständige Baum. Also gilt für jeden perfekt balancierten Baum der Größe N:

Der kleinste perfekt balancierte Baum der Tiefe d ist ein vollständiger Baum der Tiefe d-1 (mit <math>2^{(d-1)+1} - 1</math> Knoten), wo an einem einzigen Knoten noch ein weiteres Datenelement angehängt wurde (grüner Knoten in der Abbildung). Dieser Baum enthält

<math>N = \left(2^{(d-1)+1} - 1\right) + 1 = 2^d</math>

Datenelemente. Folglich gilt für perfekt balancierte Bäume die Ungleichung

und demzufolge auch

Da die Baumoperationen im ungünstigsten Fall die Komplexität <math>\mathcal{O}(d)</math> haben, gilt für perfekt balancierte Bäume, dass alle Operationen im schlechtesten Fall die Komplexität

<math>\mathcal{O}(\log(N))</math>

haben, das ist logarithmische Komplexität. Ein perfekt balancierter Baum wird z.B. durch die Datenstruktur des AVL-Baums realisiert. Die Implementation eines AVL-Baums ist jedoch kompliziert, und es zeigt sich, dass die Eingenschaft der perfekten Balance gar nicht notwendig ist, um logarithmische Komplexität zu garantieren. Wir definieren:

balancierter Baum

Für die Tiefe d(N) eines balancierten Baumes mit N Knoten gilt

<math>\forall N:d(N)\le c \cdot d_{PB}(N)</math> mit <math>1 \le c < \infty</math>

wobei d_PB(N) die Tiefe eines perfekt balancierten Baumes mit N Knoten ist. Für die Komplexität der Operationen in einem balancierten Baum gilt dann:

<math>f(N) \le c\cdot f_{PB}(N) = c\, \mathcal{O}(\log(N)) = \mathcal{O}(\log(N))</math>

d.h. die Komplexität ändert sich nicht. Balancierte Bäume sind fast genauso schnell wie perfekt balancierte Bäume (bis auf den Faktor c), aber ihr Aufbau ist algorithmisch einfacher.

Idee selbst-balencierender Bäume

Die grundlegende Idee der selbst-balancierenden Bäume besteht darin, nach jeder Einfügung die Balance des Baumes zu optimieren. Dies geschieht am zweckmäßigsten im aufsteigenden Zweig der Rekursion, also nach der Rückkehr von den rekursiven Aufrufen der Funktion treeInsert. Dies entspricht folgendem Pseudo-Code:

 def insertTree(node,key):
     if node is None: 
         return Node(key)       
     if node.key == key:
         return node
     if key < node.key:
         node.left  = insertTree(node.left, key)
     else:
         node.right = insertTree(node.right, key)    
     optimiere die Balance hier
     return node

Dabei muss man beachten, dass bei den Optimierungen die Suchbaumbedingung (Definition siehe oben) erhalten bleibt. Dies ist garantiert, wenn alle Umstrukturierungen durch die elementare Operation der Rotation implementiert werden. Eine Rechtsrotation ersetzt die Wurzel n eines Teilbaumes durch sein linkes Kind, und fügt die alte Wurzel als rechtes Kind der neuen Wurzel ein. Die Linksrotation ist die Inverse dieser Operation. Die Abbildung verdeutlicht die Umstrukturierungen:

Die Rotationen werden wie folgt implementiert:

def rotateRight(node):
    newRoot = node.left
    node.left = newRoot.right
    newRoot.right = node
    return newRoot

def rotateLeft(node):
    newRoot = node.right
    node.right = newRoot.left
    newRoot.left = node
    return newRoot

Man erkennt leicht, dass die Suchbaumbedingung erhalten bleibt. Wir erläutern dies für die Rechtsrotation, bei der Linksrotation gilt die Erklärung entsprechend. Knoten n hat einen größeren Schlüssel als Knoten L, denn L ist vor der Rechtsrotation das linke Kind von n. Nach der Rotation ist n deshalb korrekterweise das rechte Kind von L. Weiter gilt für den Teilbaum mit der Wurzel LR, dass er größer als L ist (denn er ist das rechte Kind von L), aber kleiner als n (denn er liegt im linken Teilbaum von n). Nach der Rechtsrotation ist diese Bedingung immer noch erfüllt, denn LR ist jetzt linker Teilbaum von n, welches wiederum rechter Teilbaum von L geworden ist. Alle anderen Teilbäume sind von der Rotation nicht betroffen.

Verschiedene Arten von selbst-balancierenden Bäumen unterscheiden sich im Wesentlichen dadurch, wann welche Rotation ausgeführt wird. Wichtige Beispiele sind

AVL-Bäume (älteste Variante)
Rot-Schwarz-Bäume (verbreitetste Variante)
Treaps (flexibelste Variante, siehe Übung 6.1)
Splay trees
Andersson-Bäume (einfachste Variante, siehe unten)

Daneben wird gern die Skip List verwendet, die aber kein Binärbaum ist, sondern auf einem anderen Prinzip beruht.

Andersson-Bäume

Jeder selbst-balancierende Baum benötigt Zusatzinformationen, die die augenblickliche Balance beschreiben, so dass diese gegebenenfalls optimiert werden kann. Der Andersson-Baum fügt zu diesem Zweck in jedem Knoten ein neues Feld level ein, welches mit 1 initialisiert wird:

 class AnderssonNode:
   def__init__(self, key):
       self.key = key
       self.left = selft.right = None
       self.level = 1

Grob gesprochen kodiert das level-Feld den Abstand des Knotens vom Sentinel. Genauer gelten folgende

Regeln:

Es gibt vertikale Kanten (parent.level == child.level + 1 ) und horizontale Kanten (parent.level == child.level).
Die reduzierte Länge eines Pfades zwischen zwei Knoten wird berechnet, indem nur die vertikalen Kanten im Pfad gezählt werden.
Das Sentinel hat level = 0. Alle Kanten zum Sentinel sind vertikal.
Die reduzierte Höhe eines Knotens entspricht der reduzierten Länge des Pfades von diesem Knoten zum Sentinel. Das level-Feld jedes Knotens speichert die reduzierte Höhe dieses Knotens. Folglich gilt für alle Knoten, die direkt mit dem Sentinel verbunden sind, level = 1. Insbesondere gilt dies auch für neu eingefügte Knoten (siehe obige Initialisierung).

Die nächsten zwei Regeln sichern die Balance:

Alle RS-Pfade haben die gleiche reduzierte Länge. Dies ist äquivalent zu der Bedingung, dass die Wurzel des Andersson-Baumes über alle möglichen RS-Pfade auf dem gleichen Level erreicht wird.
Kein Pfad hat 2 aufeinander folgende horizontale Kanten.

Die letzte Regel führt zu starken algorithmischen Vereinfachungen gegenüber den konzeptionell sehr ähnlichen Rot-Schwarz-Bäumen:

Nur Kanten zum rechten Kind dürfen horizontal sein.

Das folgende Bild zeigt einen Andersson-Baum, bei dem allerdings nicht alle Verbindungen zum Sentinel eingezeichnet sind:

Es gilt folgender

Satz

Jeder Andersson-Baum ist balanciert. Beweis:

1. Sei h_r die reduzierte Höhe des Andersson-Baumes. Die Eigenschaft, dass alle RS-Pfade die reduzierte Länge h_r (also die gleiche Länge) haben, hat eine wichtige Folge: Hat der Andersson-Baum keine horizontalen Kanten, so muss er ein vollständiger Baum der Tiefe d_v = h_r - 1 sein, denn nur ein vollständiger Baum hat die Eigenschaft, dass alle RS-Pfade die gleiche Länge besitzen. Gibt es hingegen horizontale Kanten, muss der Andersson-Baum mehr Elemente enthalten als der vollständige Baum der Tiefe d_v. Folglich gilt für die Anzahl der Knoten eines Andersson-Baumes:

2. Da niemals zwei aufeinenderfolgende Kanten horizontal sein dürfen, ist in jedem RS-Pfad höchstens die Hälfte aller Kanten horizontal. Daher gilt für die Tiefe d eines Andersson-Baumes

3. Fasst man 1. und 2. zusammen, erhält man:

<math>d \le 2 \log_2(N + 1)</math>.

Da die Komplexität der Baumoperationen <math>f(N) = \mathcal{O}(d)</math> ist, gilt für den Andersson-Baum:

<math>f(N) = \mathcal{O}(2 \log_2(N + 1)) = \mathcal{O}(\log(N))</math>

q.e.d.

Wie erreicht man die Balance

Der Baum ist nicht mehr balanciert, wenn obige Regeln verletzt sind. Dies kann durch Einfügen eines neuen Knotens oder durch Löschen eines Knotens passieren. Nach jeder Einfügung haben sowohl der neue Knoten als auch sein Vater das Level 1 (denn der Vater war vorher direkt mit dem Sentinel verbunden). Kanten zu neu eingefügten Knoten sind deshalb immer horizontal. Dies kann die Regeln verletzen, indem entweder

eine horizontale Kante zum linken Kind enstanden ist (falls der neue Knoten ein linkes Kind ist), oder
zwei aufeiender folgende horizontale Kanten zu rechten Kindern entstanden sind (falls der neue Knoten ein rechtes Kind ist, und sein Vater bereits ein horizontales rechtes Kind war).

Diese Fehler können durch Rotation leicht behoben werden:

Linke horizontale Kanten werden durch Rechtsrotation in rechte horizontale Kanten verwandelt.
Bei zwei aufeinander folgenden rechten horizontalen Kanten wird der mittlere Knoten um eine Ebene angehoben.

Dabei ist zu beachten, dass die erste Reparatur einen neuen Fehler erzeugen kann: Es können zwei aufeinanderfolgende rechte horizontale Kanten enstehen. Daher muss die zweite Operation stets nach der ersten ausgeführt werden. Das Anheben des Levels in der zweiten Operation kann wiederum dazu führen, dass auf der nächsthöheren Ebene verbotene horizontale Kanten entstehen. Deshalb müssen die Reparaturoperationen auf der nächsten Ebene rekursiv wiederholt werden. Dies führt uns zu folgender Implementation des Insert-Algorithmus

 def anderssonTreeInsert(node,key):
     if node is None: 
         return AnderssonNode(key)       
     if node.key == key:
         return node
     if key < node.key:
         node.left  = anderssonTreeInsert(node.left, key)
     else:
         node.right = anderssonTreeInsert(node.right, key)    
     if node.left is not None and node.level == node.left.level: # linke horizontale Kante
           node = rotateRight(node)  # wird zu rechter horizontaler Kante gemacht
     if node.right is not None and node.right.right is not None and node.level==rotate.right.right.level:  # aufeinanderfolgende horizontale Kanten
           node = rotateLeft(node)   # mache den mittleren Knoten zur Wurzel des Teilbaums
           node.level += 1           # und hebe die Wurzel um ein level an    
     return node

Da die Reparaturoperationen auf dem Rückweg von der Rekursion ausgeführt werden, ist gewährleistet, dass sie auf der nächsten Ebene des Baumes ebenfalls ausgeführt werden, falls nötig. Die folgende Skizze verdeutlicht die Anwendung der Reparaturen, wenn Knoten c über eine linke horizontale Kante an Knoten b angefügt wurde. Im oberen Beispiel genügt die erste Operation zur Reparatur, beim unteren Beispiel muss hingegen auch noch die zweite Operation angewendet werden.

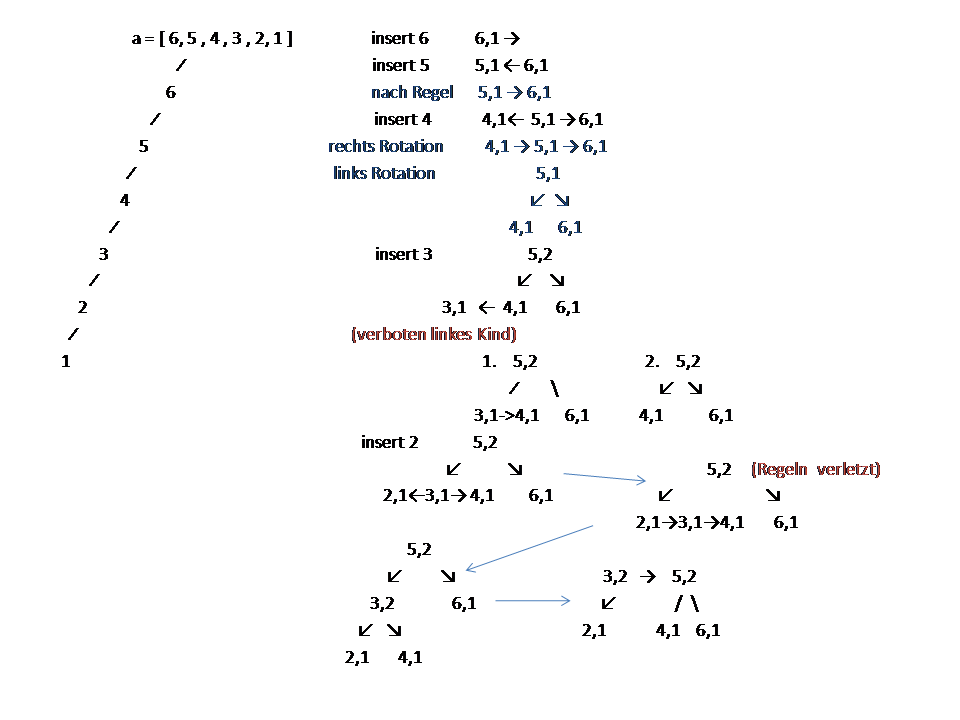
Die folgende Illustration verdeutlicht das Verhalten des Andersson-Baumes, wenn die Schlüssel in der Folge [6,5,4,3,2,1] eingefügt werden. Beim einfachen Binärbaum sind solche vorsortierten Daten sehr ungünstig und führen zu entarteten Bäumen mit linearer Zugriffzeit (links). Die Umstrukturierungen beim Andersson-Baum stellen hingegen sicher, dass die Balance immer gewahrt bleibt (rechts). Diese Illustration sollte unbedingt verbessert werden. Die entscheidenden Punkte sind sehr schwer erkennbar, und es gibt auch Fehler.

Die Löschoperation anderssonTreeRemove benötigt in jedem Knoten bis zu 5 Rotationen. Wegen der Einzelheiten verweisen wir auf Anderssons Originalartikel.

Beziehungen zwischen dem Suchproblem und dem Sortierproblem

Sortieren mit Hilfe eines selbst-balancierenden Suchbaums

Mit Hilfe eines selbst-balancierenden Suchbaums kann ein effizienter Sortieralgorithmus implementiert werden, indem man zunächst die Daten in beliebiger Reihenfolge in einen Baum einfügt, und dann in der richtigen Sortierung wieder ausliest.

  a = ...   # unsortiertes Array
  t = None  # leerer Andersson-Baum
  for e in a:
      t = anderssonTreeInsert(t, e) # Baum erzeugen
  r = []    # leeres dynamisches Array
  treeSort(t, r) 
  # r enthält jetzt die Daten aus a in sortierter Reihenfolge

Die Funktion treeSort navigiert im Sinne eines sogenannten in-order traversals durch den Baum und fügt die Datenelemente in der richtigen Reihenfolge an des Array an:

def treeSort(node,array):          # dynamisches Array als 2. Argument
    if node is None:               # <math>\mathcal{O}(1)</math>
        return
    treeSort(node.left, array)     # rekursiv
    array.append(node.key)         # amortisiert <math>\mathcal{O}(1)</math>
    treeSort(node.right, array)    # rekursiv

Komplexität

Jede Einfügeoperation in den Baum hat logarithmische Komplexität. Der Aufbau eines Baumes aus N Elementen hat daher Komplexität <math>\mathcal{O}(N \log(N))</math>.
treeSort führt in jedem Knoten eine oder zwei Operationen mit Komplexität <math>\mathcal{O}(1)</math> sowie zwei rekursive Aufrufe aus. Die Auflösung der Rekursion ergibt

<math>
f(N)=\mathcal{O}(1)+f(N_\mathrm{left})+f(N_\mathrm{right})=\mathcal{O}(1)+\mathcal{O}(1)+f(N_\mathrm{left.left})+f(N_\mathrm{left.right})+\mathcal{O}(1)+f(N_\mathrm{right.left})
+f(N_\mathrm{left.right})=N\cdot\mathcal{O}(1)=\mathcal{O}(N)
</math>

Insgesamt erhalten wir also Komplexität <math>\mathcal{O}(\max(N \log(N), N)) = \mathcal{O}(N \log(N))</math> wie bei Merge Sort. Allerdings sind der konstante Faktor sowie der Speicherverbrauch größer, so dass diese Sortiermethode in der Praxis kaum angewendet wird.

Sortieren als Suchproblem

Stellt man systematisch Fragen, die nur mit True oder False beantwortet werden können, kann dieses Vorgehen auch als Entscheidungsbaum dargestellt werden.

Als Beispiel verwenden wir den Algorithmus zum Sortieren von drei Elementen aus der Vorlesung über Sortieren. Als Eingabe sind drei Zahlen vorgegeben a={1,2,3}, deren Reihenfolge (Permutation) nicht bekannt ist. Wie die Illustration für den linke Hälfte des Entscheidungsbaumes zeigt, können wir die Reihenfolge mit nur 3 Fragen herausbekommen.
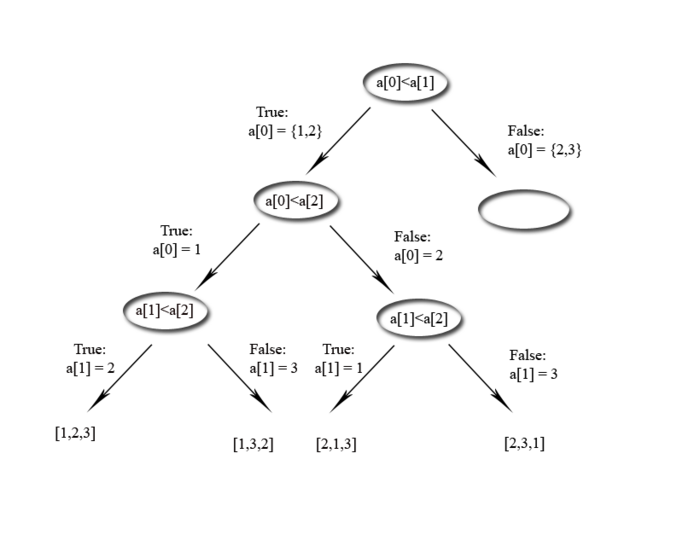
(Die Reihenfolge der Antworten True, False, True kann allerdings gar nicht auftreten, weil sie widersprüchlich ist (bitte aus der Graphik löschen!)
Die allgemeine Regel lautet: Wenn es N mögliche Lösungen gibt, muss der Baum N Blätter haben. Wie wir oben gezeigt haben, hat ein Baum mit N Blättern mindestens die Tiefe log(N).

vollständiger Baum [1]
2^d+1 Knoten
2^d Blätter

Im Fall des Sortierens von n Elementen gilt, dass es N = n! mögliche Permutation gibt. Ein Baum mit n! Blättern hat mindestens die Tiefe log(n!). Im obigen Beispiel für n=3 gilt 3! = 1*2*3 = 6 und damit für die Tiefe d

<math>d = \lceil \log_2(6)\rceil \approx \lceil 2.6\rceil = 3</math>

Im ungünstigsten Fall braucht man bei dem Frage-Baum drei Schritte. Weil aber <math>\log(6)\approx 2.6 < 3</math> muss nicht jeder Pfad zu Ende durchlaufen werden, um die Lösung zu bekommen. Allgemein gilt

Die letzte Identität gilt, weil <math>\ln(1) = 0</math> und in der Summe weggelassen werden kann. Eine untereSchranke für die Höhe kann man explizit bestimmen durch die Methode der

Abschätzung von Summen durch Integrale

Gegeben seine eine monoton wachsende Funktion f(x) (blaue Kurve). Das bestimmte Integral über die Funktion sei

<math>\int_{x_1}^{x_2} f(x)dx</math>.

Wenn wir das Funktionsargument x abrunden (schwarze Kurve), entsteht ein Integral, das einen kleineren Wert als das ursprüngliche Integral hat. Runden wir auf (rote Kurve), entsteht ein Integral mit einem größeren Wert:

<math>\int_{x_1}^{x_2} f(\lfloor x \rfloor)dx \le \int_{x_1}^{x_2} f(x)dx \le \int_{x_1}^{x_2} f(\lceil x \rceil)dx</math>

In unserem Zusammenhang sind x₁ und x₂ positive ganze Zahlen. Deshalb gilt

<math>f(\lfloor x \rfloor)_{x_1}^{x_1+1}= f(x_1),</math>

<math>f(\lfloor x \rfloor)_{x_1+1}^{x_1+2}= f(x_1+1)</math>

<math>f(\lfloor x \rfloor)_{x_2-1}^{x_2}= f(x_2-1)</math>

Wir können die obigen Integrale daher folgendermaßen vereinfachen:

<math>\begin{array}{lcl}

\int_{x_1}^{x_2} f(\lfloor x \rfloor) dx &=& \int_{x_1}^{x_1 + 1} f(\lfloor x \rfloor) dx + ...+ \int_{x_2-1}^{x_2} f(\lfloor x \rfloor) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2-1) dx \\ & = & f(x_1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2-1) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1) + ...+ f(x_2-1) \\ & = & \sum_{k=x_1}^{x_2-1} f(k) \end{array}</math> für die Fläche unter den schwarzen Rechtecken sowie

<math>\begin{array}{lcl}

\int_{x_1}^{x_2} f(\lceil x \rceil) dx &=& \int_{x_1}^{x_1 + 1} f(\lceil x \rceil) dx + ...+ \int_{x_2-1}^{x_2} f(\lceil x \rceil) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1+1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2) dx \\ & = & f(x_1+1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1+1) + ...+ f(x_2) \\ & = & \sum_{k=x_1+1}^{x_2} f(k) \end{array}</math> für die Fläche unter den roten Rechtecken. Zusammenfassend gilt also <math> \sum_{k=x_1}^{x_2-1} f(k) \le \int_{x_1}^{x_2} f(x)dx</math> und <math> \sum_{k=x_1+1}^{x_2} f(k) \ge \int_{x_1}^{x_2} f(x)dx</math> Für unser Problem setzen wir f(k) = ln(k), x₁+1 = 2, und x₂ = n. Also können wir abschätzen

Das Integral ist leicht zu lösen, und wir erhalten

<math>\frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \ge \frac{1}{\ln(2)}\left[x\ln(x)-x\right]_{x=1}^{n} = \frac{1}{\ln(2)}(n\ln(n)-n+1)=n\log_2(n) - \frac{n-1}{\ln(2)}</math>

Folglich gilt:

<math>d=\log_2(n!) = \frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \in \Omega(n \log(n))</math>

Mit anderen Worten: Kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymptotisch schneller als Mergesort, denn die Anzahl der Vergleiche (= die Höhe des Entscheidungsbaumes) ist <math>\Omega(n \log(n))</math>. Falls man einen schnelleren Sortieralgorithmus benötigt, muss man ein anderes algorithmisches Prinzip verwenden, siehe dazu Übungsaufgabe 6.2.