Suchen

Es wäre super wenn jemand ganz kurz schreiben könnte, was am Donnerstag zu den Funktionen treeInsert/Remove/HasKey gemacht wurde, was man ja für den aktuellen Übungszettel braucht. Danke :-)

Das Suchen ist eine grundlegende Operation in der Informatik. Viele Probleme in der Informatik können auf Suchaufgaben zurückgeführt werden.

Gemeint ist mit Suchen das Wiederauffinden einer oder mehrerer Datensätze aus einer Menge von früher gespeicherten Datensätzen. Ein paar einleitende Worte zum Suchproblem findet man hier.

Überblick verschiedener Suchmethoden

Um sich der Vielseitigkeit von Suchproblemen bewusst zu werden, ist es sinnvoll, sich einen Überblick über verschiedene Suchmethoden zu verschaffen.

Hier sei auch auf einen bereits existierenden Wikipedia-Artikel zu Suchverfahren verwiesen.

Allen gemeinsam ist die grundlegende Aufgabe, ein Datenelement mit bestimmten Eigenschaften aus einer großen Menge von Datenelementen zu selektieren. Dies kann, natürlich ohne jeden Anspruch auf Vollständigkeit, nach einer der jetzt diskutierten Methoden geschehen:

• Schlüsselsuche: meint das Suchen von Elementen mit bestimmtem Schlüssel; ein klassisches Beispiel wäre das Suchen in einem Wörterbuch, die Schlüssel entsprechen hier den Wörtern, die Datensätze wären die zu den Wörtern gehörigen Eintragungen.

• Bereichssuche: im Allgemeinen meint die Bereichssuche in n-Dimensionen die Selektion von Elementen mit Eigenschaften aus einem bestimmten n-dimensionalen Volumen. Im eindimensionalen Fall will man alle Elemente finden, deren Eigenschaft(en) in einem bestimmten Intervall liegen. Die Verallgemeinerung auf n-Dimensionen ist offensichtlich. Ein Beispiel für die Bereichssuche in einer 3D-Kugel wäre ein Handy mit Geolokalisierung, welches alle Restaurants in einem Umkreis von 500m findet. Lineare Ungleichungen werden durch graphisch durch Hyperebenen repräsentiert. In 2D sind diese Hyperebenen Geraden. Die Ungleichungen können dann den Lösungsraum in irgendeiner Form begrenzen.

• Ähnlichkeitssuche: finde Elemente, die gegebenen Eigenschaften möglichst ähnlich sind. Ein prominentes Beispiel ist Google oder das Suchen des nächsten Restaurants.

• Graphensuche: Hier wäre beispielsweise das Problem optimaler Wege zu nennen (Navigationssuche). Dieser Punkt wird später im Verlauf der Vorlesung noch einmal aufgegriffen werden.

Im jetzt Folgenden wird nur noch die Schlüsselsuche betrachtet werden.

Sequentielle Suche

Die sequentielle oder lineare Suche ist die einfachst mögliche Methode, einen Datensatz zu durchsuchen. Hierbei wird ein Array beispielsweise sequentiell von vorne nach hinten durchsucht. Ein prinzipieller Vorteil der Methode ist, dass auf der Eigenschaft der Datenelemente, nach denen das Array durchsucht wird, keine Ordnung im Sinne von > oder < definiert zu sein braucht, lediglich die Identität (==) muss feststellbar sein. Der folgende (Pseudo)-Python-Code zeigt eine Implementation der Suchmethode.

a = ... # array
len(a) == N
foundIndex = seqSearch(a, key) 
# foundIndex == -1 wenn nichts gefunden, 0 <math>\leq </math> foundIndex <math> \leq </math> N wenn key gefunden (erster Eintrag mit diesem Wert)

def SeqSearch(a, key):
   for i in range(len(a)):
       if a[i] == key:  # bzw. allgemeiner a[i].key == key 
           return i
   return -1

Wir wollen jetzt die Komplexität dieses Algorithmus bestimmen.

Nimmt man an, dass der innerste Vergleich (a[i] == key) jeweils <math> \mathcal{O}(1)</math> ist - was dann sinnvoll ist, wenn der Vergleichsoperator nicht überladen und somit evtl. komplexer ist. Dieser Vergleich wird in der for-Schleife jeweils N-mal durchgeführt (<math> \mathcal{O}(N)</math>), so dass man nach der Verschachtelungsregel eine gesamte Komplexität von <math> \mathcal{O}(N)</math> erhält.

Der Name lineare Suche rührt von diesem linearen Anwachsen der Komplexität mit der Arraygröße her.

Binäre Suche

Wie wir weiter unten zeigen werden, gestattet es diese Suchmethode, die Gesamtdauer der Suche in großen Datensätzen beträchtlich zu verringern. Die Methode beruht auf dem Divide and Conquer-Prinzip, wobei die Suche in jedem Schritt rekursiv auf eine Hälfte des Datensatzes eingeschränkt wird. Weitere Details zur Methode sind hier zu finden.

Die Methode ist nur dann anwendbar beziehungsweise effektiv, wenn folgendes gilt:

1. Auf der Eigenschaft der Daten, die zur Suche verwendet wird, ist eine Ordnung im Sinne von < oder > definiert.
2. Wir wollen uns auf Datensätze beschränken, die schon fertig aufgebaut sind, in die also keine neuen Elemente mehr eingefügt werden wenn man mit dem Suchen beginnt. Ist dies nicht der Fall, so ist unter Umständen die Implementierung über einen Binärbaum

(siehe auch weiter unten) geschickter.

Der folgende Algorithmus zeigt eine beispielhafte Implementierung der Methode:

a = []   # array
len(a) == N
a.sort()  # sortiere über Ordnung des Schlüssels
foundIndex = binSearch(a, key, 0, len(a))  # (Array, Schlüssel, von wo bis wo suchen im Array)

def binSearch(a, key, start, end):  # start ist 1. Index, end ist letzter Index + 1
   size = end - start   # <math> \mathcal{O}(1)</math>
   if size <= 0:   # Bereich leer?  <math> \mathcal{O}(1)</math>
       return -1   # <math> \mathcal{O}(1)</math>
   center = (start + end)/2   # Integer Division, Ergebnis wird abgerundet, wichtig für ganzzahlige Indizes <math> \mathcal{O}(1)</math>
   if a[center] == key:  # <math> \mathcal{O}(1)</math>
       return center  # <math> \mathcal{O}(1)</math>
   elif a[center] < key:  <math> \mathcal{O}(1)</math>
       return binSearch(a, key, center + 1, end)  # Rekursion
   else:
       return binSearch(a, key, start + 1, center)  # Rekursion

Zur Berechnung der Komplexität dieses Algorithmus vernachlässigen wir zunächst den Aufwand, den die Sortierung weiter oben verursacht. Dieser Schritt mag oder mag nicht zulässig sein.

Nach der Sequenzregel haben auch alle <math>\mathcal{O}(1)</math> Anweisungen die Komplexität <math>\mathcal{O}(1)</math>. Es bleibt die Komplexität der Rekursion zu berechnen. Die gesamte Komplexität des Algorithmus (jetzt als Funktion f bezeichnet) setzt sich zusammen aus den oben erwähnten <math>\mathcal{O}(1)</math> Anweisungen sowie der Rekursion und ist

<math>f(N) = \mathcal{O}(1) + f(N/2) = \mathcal{O}(1) + \mathcal{O}(1) + f(N/4) = ... = \underbrace{\mathcal{O}(1) + ... + \mathcal{O}(1) + \underbrace{f(0)}_{\mathcal{O}(1)\, \rightarrow \,\mathrm{size-Abfrage}}}_{n+1 \,\mathrm{Terme}} </math>

Falls jetzt gilt <math> N = 2^n </math>

<math> \rightarrow f(N) = \mathcal{O}(1) \cdot \mathcal{O}(n+1) = \mathcal{O}(n) = \mathcal{O}(\lg N) </math>

Für große Datenmengen ist die binäre Suche also weit effizienter als die lineare Suche. Verdoppelt sich beispielsweise die zu durchsuchende Datenmenge, so verdoppelt sich der Aufwand für die sequentielle Suche - bei der binären Suche hingegen benötigt man lediglich eine zusätzliche Vergleichsoperation.

Für kleine Daten jedoch (<math> N = 4, 5 </math>) ist die sequentielle Suche jedoch schneller als die binäre Suche, da hier die rekursiven Funktionsaufrufe teurer als das Mehr an Vergleichen sind.

Eine relativ einfache Möglichkeit, die binäre Suche zu verbessern, ist die sogenannte Interpolationssuche. Hierbei wird die neue Position für die Suche, also die Mitte des Arrays, durch eine Schätzung ersetzt, die angibt, wo sich der Schlüssel innerhalb des Arrays befinden könnte. Bei der Suche in einem Telefonbuch nach dem Namen Zebra würde man ja auch nicht in der Mitte anfangen. Näheres hierzu im Buch von Sedgewick.

Um sich den Algorithmus der binären Suche klar zu machen, ist es instruktiv, sich die folgende Tabelle genauer anszusehen:

key	start	end	size	center	return	Kommentare
4	0	5	5	2	2
2	0	5	5	2		linker Randfall
	0	2	2	1
	0	1	1	0	0	gefunden
1	0	5	5	2		links außerhalb
	0	2	2	1
	0	1	1	0
	0	0	0		-1	rechter Randfall
6	0	5	5	2
	3	5	2	4	4
5	0	5	5	2		typischer Fall
	3	5	2	4
	3	4	1	3	3
7	0	5	5	2		rechts außerhalb
	3	5	2	4
	5	5	0		-1

Suche in einem Binärbaum

Eine kurze Einführung in Binärbäume findet man hier.

Bäume sind zweidimensional verkettete Strukturen. Sie gehören zu den fundamentalen Datenstrukturen in der Informatik. Da man in Bäumen nicht nur Daten speichern kann, sondern auch relevante Beziehungen der Daten untereinander, festgelegt über eine Ordnung auf der vergleichenden Dateneigenschaft, eignen sich Bäume also insbesondere, um gesuchte Daten schnell wieder auffinden zu können.

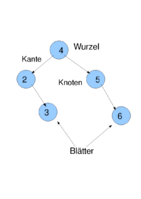
Ein Binärbaum wie oben skizziert besteht aus einer Menge von Knoten, die untereinander durch Kanten verbunden sind. Jeder Knoten hat einen linken und einen rechten Unterbaum, der auch leer sein kann (in Python ließe sich dies mit None implementieren). Führt eine Kante von Knoten A zu Knoten B, so heißt A Vater von B und B Kind von A. Es gibt genau einen Knoten ohne Vater, den man Wurzel nennt. Knoten ohne Kinder heißen Blätter.

Ein Suchbaum