Randomisierte Algorithmen
1. Randomisierte Algorithmen
Def.: Algorithmen, die bei Entscheidung oder bei der Wahl der Parameter Zufallszahlen benutzen
Bsp.: Lösen des K-SAT-Problems durch RA
geg.: logischer Ausdruck in K-CNF (n Variablen, m Klauseln, k Variablen pro Klausel)
<math>\underbrace {\underbrace {\left(x_1 \vee x_3 \vee...\right)}_{k\; Variablen} \wedge \left( x_2 \vee x_4 \vee...\right)}_{m\;Klauseln}</math>
for i in range (trials): #Anzahl der Versuche
#Bestimme eine Zufallsbelegung des <math>\{ x_i \}</math>:
for j in range (steps):
if <math>\{ x_i \}</math> erfüllt alle Klauseln: return <math>\{ x_i \}</math>
#wähle zufällig eine Klausel, die nicht erfüllt ist und negiere zufällig eine der Variablen in dieser Klausel
(die Klausel ist jetzt erfüllt)
return None
Eigenschaft: falls <math>k>2</math> : steps *trials <math>\in O\left(\Alpha^n \right) \Alpha >1</math>
z.B. <math>k=3</math> steps=3*n, trials=<math>\left(\frac{4}3\right)^n</math>
aber: bei <math>k=2</math> sind im Mittel nur steps=<math>O\left(n^2\right)</math> nötig, trials=<math>O\left(1\right)</math>
-Zufallsbelegung hat <math>t\leq n</math> richtige Variablen (im Mittel <math>t\approx \frac {n} 2</math>)
Negieren einer Variable ändert t um 1, u.Z. <math>t\rightarrow t+1</math> mit Wahrscheinlichkeit <math>\frac 1 2</math> ::(für beliebiges k: <math>\frac 1 k</math>)
- <math>t\rightarrow t-1</math> mit Wahrscheinlichkeit <math>\frac 1 2</math> ::(für beliebiges k: <math>\frac {k-1} k</math>)
-Wieviele Schritte braucht man im Mittel, um zu einer Lösung mit t Richtigen zu kommen?
<math>S\left(t\right)=\frac 1 2 S\left(t-1\right) + \frac 1 2 S\left(t+1\right) +1</math>
<math>S\left(n\right)=0</math> #Abbruchbedingung der Schleife
<math>S\left(0\right) = S\left( 1\right) + 1 \Rightarrow S\left(t\right) = n^2-t^2</math>
Probe:
<math>
\begin{align}
S\left(n\right) & = n^2-n^2=0 \\
S\left(0\right) &= n^2-0^2 \\
&= S\left(1\right)+1 \\
&= n^2-1^2+1 \\
&= n^2 \\
S\left(t\right) &= \frac 1 2 \left(n^2-\left(t-1\right)^2\right) + \frac 1 2 \left(n^2-\left(t+1\right)^2\right)+1 \\
&= \frac 1 2 n^2-\frac 1 2 \left( t^2-2t+1\right) + \frac 1 2 n^2-\frac 1 2 \left(t^2+2t+1\right) + 1 \\
&= n^2-t^2
\end{align}</math>
Das ist das Random Walk Problem
Im ungünstigsten Fall (t=0) werden im Mittel <math>n^2</math> Schritte benötigt, um durch random walk nach t=n zu gelangen.
2. RANSAC-ALGORITHMUS (Random Sample Consensus)
Aufgabe: gegeben: Datenpunkte
- gesucht: Modell, das die Datenpunkte erklärt
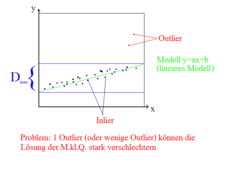
Messpunkte:
übliche Lösung: Methode der kleinsten Quadrate
<math>\min_{a,b} \sum_{i} \left(a x_i + b + y_i\right)^2</math>
Schulmathematik: <math>Minimum\stackrel{\wedge}{=}Ableitung=0</math>
Lineares Gleichungssystem
<math>\frac{d}{da}\sum{i} \left(ax_i+b-y_i\right)^2=\sum{i} \frac{d}{da} \left[ax_i+b-y_i\right)^2</math>
- <math>f\left(g\left(x\right)\right)</math>
- <math>f\left(x\right)=x^2</math>
- <math>y\left(a\right)=ax_i+b-y_i</math>
<math>=\sum_{i}2\left(ax_i+b-y_i\right)\frac{d}{da} \underbrace {ax_i+b-y_i}_{x_i}</math>
<math>\underline {=2\sum_{i}\left(ax_i+b-y_i\right)x_i\stackrel{!}{=}0}</math>
- <math>a\sum_{i}{x_i}^2+b\sum_{i}x_i=\sum_{i}x_iy_i</math>
- <math>a\sum_{i}x_i+b\sum_{i}1=\sum_{i}y_i</math>
<math>\frac{d}{db}\sum_{i}\left(ax_i+b-y_i\right)^2=2\sum_{i}\left(ax_i+b-y_i\right)*1</math>
- Problem: <math>\epsilon %</math> der Datenpunkte sind Outlier
- <math>\Longrightarrow</math> Einfaches Anpassen des Modells an die Datenpunkte funktioniert nicht
- Seien mindestens k Datenpunkte notwendig, um das Programm anpassen zu können
RANSAC-Algorithmus
for l in range (trials):
wähle zufällig k Punkte aus
passe das Modell an die k Punkte an
zähle, wieviele Punkte in der Nähe des Modells liegen (d.h. <math>d_i < d_max</math> muss geschickt gewählt werden)
#Bsp. Geradenfinden:-wähle a,b aus zwei Punkten
-berechne: <math>|ax_i+b-y_i|=d_i</math>
-zähle Punkt i als Inlier, falls <math>d_i<d_ma</math>
return: Modell mit höchster Zahl der Inlier
<math>trials= \frac{log\left(1-p\right)}{log\left(1-\left(1-\epsilon\right)^k\right)}</math> mit k=Anzahl der Datenpunkte und p=Erfolgswahrscheinlichkeit, <math>\epsilon</math>=Outlier-Anteil
Erfolgswahrscheinlichkeit: p=99%
<math>\begin{array}{|c||c|c|c|c|c|}
Beispiel & k & \epsilon=10% & 20% & 50% & 70%\\
\hline
Linie\;in\;2D & 2 & 3 &5 & 17 & 49\\
Kreis\;in\;2D & 3 & 4 & 7 & 35 & 169\\
Ebene\;in\;3D & 8 & 9 & 26 & 1172 & 70188\\
\end{array}</math>
Ein Spiel: Wie viel Schritte braucht man im Mittel zum Ziel?
geg.: 5 Plätze, 2 Personen: eine Person rückt vom einem Platz zu dem enderen Platz;
die zweite Person wirft die Münze.
Wenn die Münze auf Kopf landet, rücke nach rechts und wenn die Münze auf Zahl landet, rücke nach links.
<--- Zahl Kopf-->
Kopf: /////
Zahl: ///
- => mit 8 Schritten bis zum Ziel
- im Mittel: bei N Plätzen braucht man N2 Schritte
- all: mit N2 Schritten um N Plätze rücken
- Wie viel Schritte braucht man im Mittel zum Ziel?
<math>S\left(N\right)=0</math> #wenn wir uns im Stuhl Nr.1 befinden
<math>S\left(i\right)=\frac 1 2 S\left(1 + S\left(i+1\right)\right) + \frac 1 2 S\left(1 + S\left(i-1\right)\right) = \frac 1 2 S\left(i+1\right) + \frac 1 2 S\left(i-1\right) +1 </math>
<math>S\left(0\right)=1 + S\left(1\right)</math> #bei 0.Platz
- Lösung:
<math>S\left(i\right)= N^2 - i^2</math>
- speziell:
<math>S\left(i\right)= N^2</math> #wenn man am ungünstigsten Platz startet
Beziehung zu randomisiertem 2-SAT
"Platz <math>i</math> ": <math>i</math> Variablen haben den richtigen Wert, <math>\left(N-i\right)</math> sind falsch gesetzt
<math>S\left(\frac N 2\right)=N^2 - \left(\frac N 2\right)^2 = N^2 - \frac N 4 ^2 = \frac 3 4 N^2 </math>
<math>S\left(\frac N 2\right)</math> # Anfangszustand
Las Vegas vs. Monte Carlo
* Las Vegas - Algorithmen
- Ergebnis ist immer korrekt.
- Berechnung ist mit hoher Wahrscheinlichkeit effizient (d.h. Randomisierung macht den ungünstigsten Fall unwahrscheinlich).
* Monte Carlo - Algorithmen
- Berechnung immer effizient.
- Ergebnis mit hoher Wahrscheinlichkeit korrekt (falls kein effizienter Algorithmus bekannt, der immer die richtige Lösung liefert).
| Las Vegas | Monte Carlo |
|---|---|
| - Erzeugen einer perfekten Hashfuktion | - Algorithmus von Freiwald(Matrizenmultiplikation) |
| - universelles Hashing | - RANSAC |
| - Quick Sort mit zufälliger Wahl des Pivot-Elements | - randomisierte K-SAT(k>=3)(Alg. von Schöning) |
| - Treep mit zufälligen Prioritäten | - |
Zufallszahlen
- - kann man nicht mit deterministischen Computern erzeugen
- - aber man kann Pseudo-Zufallszahlen erzeugen, die viele Eigenschaften von echten Zufallszahlen haben
- * sehr ähnlich zum Hash
"linear Conguential Random number generator"
<math>I_{i+1}= \left(a*I_i + c\right)mod m</math>
<math>\begin{array}{ll}
\mathrm{=> } & I_i \in [0, m-1]\\
\end{array}</math>
- -sorgfältige Wahl von a, c, m notwendig
- Bsp. m = 232
- a = 1664525, c = 1013904223
- "quick and dirty generator"
- Bsp. m = 232
Nachteile
- nicht zufällig genug für viele Anwendungen
- Bsp. wähle Punkt in R3
- <math>\begin{array}{ll}
\mathrm{ } & p = (rand(), rand(), rand())\\
\end{array}</math>
- gibt Zahl u, v, w so, dass
- <math>\begin{array}{ll}
\mathrm{ } & u * p[0] + v * p[1] + w * p[3]\\
\end{array}</math>
- stark geclustert ist.
- Periodenlänge ist zu kurz:
- spätestens nach m Schritten wiederholt sich die Folge
- allgemein: falls der interne Zustand des Zufallsgenerators k bits hat, ist Periodenlänge:
- <math>\begin{array}{ll}
\mathrm{ } & Periode < 2^k\\
\end{array}</math>
- lowbits sind weniger zufällig als die highbits
Mersenne Twister
bester zur Zeit bekannter Zufallszahlengenerator (ZZG)
- innere Zustand: <math>\begin{array}{ll}
\mathrm{ } & 624*32 bit\ Integers => 19968 bits\\
\end{array}</math>
- Periodenlänge: <math>2^ {19937} \approx 4 * 10^{6000}</math>
- Punkte aus aufeinanderfolgende Zufallszahlen in <math>\mathbb{R}^n</math> sind gleich verteilt bis <math>\begin{array}{ll}
\mathrm{ } & n = 623\\
\end{array}</math>
- alle Bits sind unabhängig voneinander zufällig ("Twister")
- schnell
class MersenneTwister:
def __init__(self, seed):
self.N = 624 # Größe des inneren Zustands festlegen
self.i = 0 # zählt mit in welchem Zustand wir uns gerade aufhalten
self.state = [0]*self.N # Speicher für den inneren Zustand reservieren
# inneren Zustand mit einfachem Zufallszahlengenerator initialisieren
self.state[0] = seed # initiale Zufallszahl vom Benutzer
for i in xrange(1, self.N):
self.state[i] = (1812433253 * (self.state[i-1] ^ (self.state[i-1] >> 30)) + i) % 4294967296
def __call__(self):
"""gibt die nächste Zufallszahl im Bereich [0, 2**32-1] aus"""
N, M = self.N, 397
# Zustand aktualisieren (neue Zufallszahl ausrechnen)
i = self.i
r = ((self.state[i] & 0x80000000) | (self.state[(i+1)%N] & 0x7FFFFFFF)) >> 1
if self.state[(i+1)%N] & 1:
r ^= 0x9908B0DF
self.state[i] = self.state[(i+M)%N] ^ r
# aktuelle Zufallszahl auslesen und ihre Zufälligkeit durch verwürfeln der Bits verbessern
y = self.state[i]
y ^= (y >> 11)
y ^= ((y << 7) & 0x9D2C5680)
y ^= ((y << 15) & 0xEFC60000)
y ^= (y >> 18)
# Zustand weitersetzen und endgültige Zufallszahl ausgeben
self.i = (self.i + 1) % N
return y
geg.: Zufallszahl
<math>\begin{array}{ll}
\mathrm{ } & [0, \overbrace{2^{32}-1}^{m-1}]\\
\end{array}</math>
ges.: Zufallszahl <math>\begin{array}{ll}
\mathrm{ } & [0, k - 1]\\
\end{array}</math>
naive Lösung: <math>\begin{array}{ll}
\mathrm{ } & rand()%k\\
\end{array}</math> ist schlecht.
Bsp. <math>\begin{array}{ll}
\mathrm{ } & \qquad m = 16\qquad k = 11\\
\end{array}</math>
| rand() | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rand()%k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 0 | 1 | 2 | 3 | 4 |
=> 0,...,n kommt doppelt so häufig wie 5,...,10 "nicht zufällig"
Lösung: Zurückweisen des Rests der Zahlen (rejektion sampling)
<math>\begin{array}{ll}
\mathrm{ } & remainder = (m - 1 - (k - 1))% k = (m - k)%k\\
\mathrm{ } & last\ Good\ Value = m-1-remainder\\
\end{array}</math>
r = rand()
while r > last.GoodValue:
r = rand()
return r%k