Sortieren in linearer Zeit
under construction
Wir kehren an dieser Stelle nochmals zum Sortierproblem zurück und stellen uns die Frage, ob wir noch schnellere Algorithmen finden können, die eventuell sogar in O(N) statt in O(N*log(N))zum Ziel kommen. Mit Hilfe der gerade eingeführten Suchbäumen werden wir zeigen, dass dies nicht möglich ist, solange für die Sortierschlüssel nur eine paarweise Vergleichsfunktion definiert ist. Besitzen wir jedoch zusätzliche Informationen über die Schlüssel, die uns die Anwendung des Bucket-Prinzips erlauben, ist das Sortieren in linearer Zeit möglich.
Sortieren und Permutationen
Bevor wir die Grenzen des Sortierens mit Paarvergleichen analysieren, wollen wir noch etwas näher beleuchten, was beim Sortieren eigentlich geschieht. Dazu gehen wir noch einen Schritt zurück und schauen uns an, was beim Mischen eines zunächst sortierten Arrays passiert. Wir betrachten das Array mit den drei Element A, B, C sowie ein korrespondierendes Indexarray, das angibt, an welcher Position im sortierten Array die drei Elemente gehören. Solange das Hauptarray noch sortiert ist, enthält das Indexarray einfach die aufsteigende Folge 0, 1, 2:
L = A B C # Hauptarray sortiert (0. Permutation) I = 0 1 2 # Indexarray
Es gibt jetzt 5 weitere Anordnungsmöglichkeiten (imsgesamt also 6 = 3! Permutationen) für die drei Elementa A, B und C. Immer, wenn wir diese drei Elemente umordnen, ordnen wir das Indexarray so, dass das Element I[k] in jedem Indexarray uns angibt, wo sich der Buchstabe jetzt befindet, der ursprünglich (also in der sortierten Anordnung) an Position k stand:
L = A C B # 1. Permutation I = 0 2 1
L = B A C # 2. Permutation I = 1 0 2
L = B C A # 3. Permutation I = 2 0 1
L = C A B # 4. Permutation I = 1 2 0
L = C B A # 5. Permutation I = 2 1 0
In der 5. Permutation sagt beispielsweise I[0] = 2, dass der ursprünglich 0. Buchstabe (das A) jetzt an Position 2 ist. Daraus folgt, dass wir ein permutiertes Array in linearer Zeit sortieren können, wenn uns das Indexarray bekannt ist. Wir müssen einfach einmal durch das Indexarray gehen und jedes Element von Position I[k] wieder an Position k verschieben:
def sortByIndexArray(L, I):
R = [None]*len(L) # zunächst leeres Ergebnisarray
for k in xrange(len(L)):
R[k] = L[I[k]] # Elemente sortiert in R einfügen
return R
Da man nur einmal über den Bereich k = 0 ... len(L)-1 gehen muss, ist der Aufwand dieser Funktion O(len(L)), also linear. Dieser Algorithmus ist z.B. nützlich, wenn man mehrere Arrays in der gleichen Weise sortieren muss, z.B. die Liste der Studentennamen und die Liste der dazugehörigen Übungspunkte. Man kann dann einfach einmal die Permutation des Indexarrays bestimmen, und dann alle Listen entsprechend sortieren. Wie man das Indexarray mit dem Standard-Sortieralgorithmus array.sort() bestimmen kann, ist Aufgabe im Übungsblatt 9.
Sortieren als Suchproblem
Wir haben gesehen, dass wir in linearer Zeit sortieren können, wenn uns die Permutation bzw. das zugehörige Indexarray bekannt ist. Die nächste Frage lautet deshalb: Wie viele Schritte brauchen wir, um die Permutation zu finden? Dabei ist es nur erlaubt, Schlüssel paarweise zu vergleichen, und man erhält jeweils eine ja/nein Antwort. Ein solches Vorgehen kann als Entscheidungsbaum dargestellt werden. Jeder Knoten ist eine Frage, und wir gehen zum linken Kind weiter, wenn die Frage mit "ja" beantwortet wurde, ansonsten zum rechten Kind. An jeder Kante stehen die jetzt noch in Frage kommenden Permutationen, und der jeweilige Kindknoten gibt uns die nächste Frage vor. Die Blätter enthalten das Indexarray, das der Permutation entspricht:
(L[0] < L[1])
ja / \ nein
ABC / \ BAC
ACB / \ CAB
BCA / \ CBA
/ \
(L[0] < L[2]) (L[0] < L[2])
/ \ / \
ja / nein \ / ja \ nein
ABC / BCA | | BAC \ CAB
ACB / | | \ CBA
/ (2 0 1) (1 0 2) \
(L[1] < L[2]) (L[1] < L[2])
/ \ / \
ja / \ nein ja / \ nein
ABC / \ ACB CAB / \ CBA
/ \ / \
(0 1 2) (0 2 1) (1 2 0) (2 1 0)
Der Suchaufwand im schlimmsten Fall entspricht offensichtlich der Tiefe des Baumes. Bei Arrays mit drei Elementen ist die Tiefe gerade 3, wir benötigen maximal 3 Fragen bis zum Ziel. Für Arrays der Länge N gilt allgemein: Es gibt M = N! verschiedene Permutationen, der Baum muss also N! Blätter haben. Wir haben im Abschnitt Suchen gesehen, dass die Tiefe eines Baumes minimal wird, wenn der Baum perfekt balanciert ist, und dass der balancierte Baum mit den meisten Blättern der vollständige Baum ist. Die Tiefe des vollständigen Baums mit N! Blättern gibt uns also eine untere Schranke für die minimale Anzahl der Vergleiche im schlechtesten Fall.
Ein vollständiger Baum der Tiefe d hat 2d+1 Knoten und 2d Blätter:
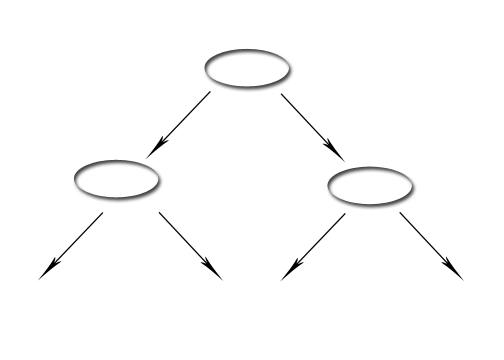 |
vollständiger Baum 2d+1 Knoten 2d Blätter |
Im Fall des Sortierens von n Elementen gilt, dass es N = n! mögliche Permutation gibt. Ein Baum mit n! Blättern hat mindestens die Tiefe log(n!). Im obigen Beispiel für n=3 gilt 3! = 1*2*3 = 6 und damit für die Tiefe d
- <math>d = \lceil \log_2(6)\rceil \approx \lceil 2.6\rceil = 3</math>
Im ungünstigsten Fall braucht man bei dem Frage-Baum drei Schritte. Weil aber <math>\log(6)\approx 2.6 < 3</math> muss nicht jeder Pfad zu Ende durchlaufen werden, um die Lösung zu bekommen.
Allgemein gilt
- <math>d \ge \log_2(n!) = \log_2(1\cdot 2\cdot ... \cdot n) = \log_2(1) + \log_2(2) + ... + \log_2(n) = \sum_{k=1}^n \log_2(k) = \frac{1}{\ln(2)}\sum_{k=1}^n \ln(k) = \frac{1}{\ln(2)}\sum_{k=2}^n \ln(k)</math>
Die letzte Identität gilt, weil <math>\ln(1) = 0</math> in der Summe weggelassen werden kann. Eine untere Schranke für die Tiefe kann man explizit bestimmen durch die Methode der
Abschätzung von Summen durch Integrale
Gegeben sei eine monoton wachsende Funktion f(x) (blaue Kurve). Das bestimmte Integral über die Funktion sei
- <math>\int_{x_1}^{x_2} f(x)dx</math>.
Wenn wir das Funktionsargument x abrunden (schwarze Kurve), entsteht ein Integral, das einen kleineren Wert als das ursprüngliche Integral hat. Runden wir auf (rote Kurve), entsteht ein Integral mit einem größeren Wert:
 |
<math>\int_{x_1}^{x_2} f(\lfloor x \rfloor)dx \le \int_{x_1}^{x_2} f(x)dx \le \int_{x_1}^{x_2} f(\lceil x \rceil)dx</math> |
In unserem Zusammenhang sind x1 und x2 positive ganze Zahlen. Deshalb gilt
- <math>f(\lfloor x \rfloor)_{x_1}^{x_1+1}= f(x_1),</math>
- <math>f(\lfloor x \rfloor)_{x_1+1}^{x_1+2}= f(x_1+1)</math>
- <math>...</math>
- <math>f(\lfloor x \rfloor)_{x_2-1}^{x_2}= f(x_2-1)</math>
Wir können die obigen Integrale daher folgendermaßen vereinfachen:
- <math>\begin{array}{lcl}
\int_{x_1}^{x_2} f(\lfloor x \rfloor) dx &=& \int_{x_1}^{x_1 + 1} f(\lfloor x \rfloor) dx + ...+ \int_{x_2-1}^{x_2} f(\lfloor x \rfloor) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2-1) dx \\ & = & f(x_1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2-1) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1) + ...+ f(x_2-1) \\ & = & \sum_{k=x_1}^{x_2-1} f(k) \end{array}</math> für die Fläche unter den schwarzen Rechtecken sowie
- <math>\begin{array}{lcl}
\int_{x_1}^{x_2} f(\lceil x \rceil) dx &=& \int_{x_1}^{x_1 + 1} f(\lceil x \rceil) dx + ...+ \int_{x_2-1}^{x_2} f(\lceil x \rceil) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1+1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2) dx \\ & = & f(x_1+1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1+1) + ...+ f(x_2) \\ & = & \sum_{k=x_1+1}^{x_2} f(k) \end{array}</math> für die Fläche unter den roten Rechtecken. Zusammenfassend gilt also <math> \sum_{k=x_1}^{x_2-1} f(k) \le \int_{x_1}^{x_2} f(x)dx</math> und <math> \sum_{k=x_1+1}^{x_2} f(k) \ge \int_{x_1}^{x_2} f(x)dx</math> Für unser Problem setzen wir f(k) = ln(k), x1+1 = 2, und x2 = n. Also können wir abschätzen
- <math>\sum_{k=x_1+1}^{x_2} f(k) = \frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \ge \frac{1}{\ln(2)}\int_1^n \ln(x) dx</math>
Das Integral ist leicht zu lösen, und wir erhalten
- <math>\frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \ge \frac{1}{\ln(2)}\left[x\ln(x)-x\right]_{x=1}^{n} = \frac{1}{\ln(2)}(n\ln(n)-n+1)=n\log_2(n) - \frac{n-1}{\ln(2)} \in \Omega(n \log(n))</math>
Folglich gilt:
- <math>d\ge\log_2(n!) = \frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \in \Omega(n \log(n))</math>
Mit anderen Worten: Kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymptotisch schneller als Mergesort, denn die Anzahl der Vergleiche (= Tiefe des Entscheidungsbaumes) ist <math>\Omega(n \log(n))</math>. Falls man einen schnelleren Sortieralgorithmus benötigt, muss man ein anderes algorithmisches Prinzip verwenden, siehe dazu Übungsaufgabe 6.2.
Bucket Prinzip
Mit dem Bucket Prinzip verteilt man die Schlüssel geschickt auf die "Fächer" (buckets) und arbeitet dann mit jedem Bucket einzeln.
1) Die Schlüssel sind bereits ganze Zahlen von [0, M)
def integerSort(a, M):
buckets = [[] for k in xrange(M)] #leere buckets
for k in xrange(len(a)):
b[a[k].key].append(a[k]) #verteilen
i = 0
for k in xrange(M):
a[i : i+len(b[k])] = b[k]
i += len(b[k])
2) Schlüssel sind keine integer
- -> umwandeln in [0, M)
- - entweder Ordnung erhalten key1 <= key2
- bucketMap(key1) <= bucketMap(key2)
- -> "Quantisierung"
- - entweder Ordnung erhalten key1 <= key2
- - oder Ordnung nicht erhalten
- -> "Hashing"
- - oder Ordnung nicht erhalten
Bucket Sort
Bucket Sort sortiert die keys in die buckets.
def bucketSort(a, bucketMap, c):
M = int(c * len(a))
b = [[] for k in xrange(M)]
for k in xrange(len(a)):
index = bucketMap(a[k].key, M)
b[index].append(a[k])
i = 0
for k in xrange(M):
insertionSort(b[k])
a[i : i + len(b[k])] = b[k]
i+= len(b[k])
Beispiel:
keys sind reelle Zahlen in [0, 1)
def bucketMap(key, M):
return int(key + M)