Sortieren in linearer Zeit

under construction

Sortieren als Suchproblem

Stellt man systematisch Fragen, die nur mit True oder False beantwortet werden können, kann dieses Vorgehen auch als Entscheidungsbaum dargestellt werden.

Als Beispiel verwenden wir den Algorithmus zum Sortieren von drei Elementen aus der Vorlesung über Sortieren. Als Eingabe sind drei Zahlen vorgegeben a={1,2,3}, deren Reihenfolge (Permutation) nicht bekannt ist. Wie die Illustration für den linke Hälfte des Entscheidungsbaumes zeigt, können wir die Reihenfolge mit nur 3 Fragen herausbekommen.
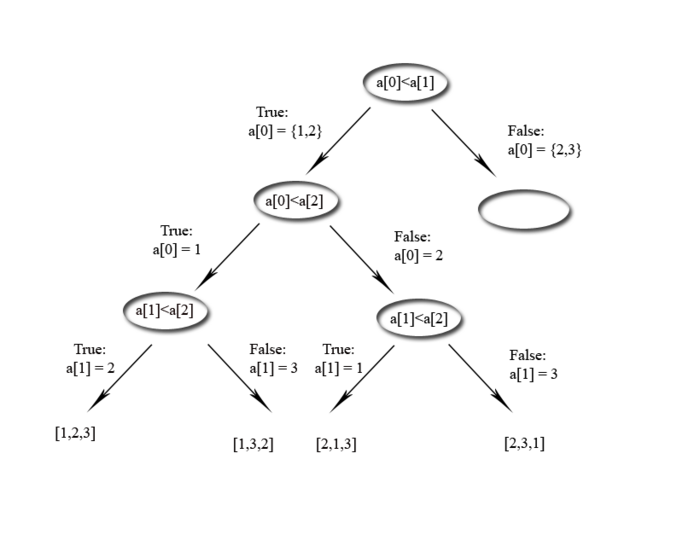
(Die Reihenfolge der Antworten True, False, True kann allerdings gar nicht auftreten, weil sie widersprüchlich ist (bitte aus der Graphik löschen!)
Die allgemeine Regel lautet: Wenn es N mögliche Lösungen gibt, muss der Baum N Blätter haben. Wie wir oben gezeigt haben, hat ein Baum mit N Blättern mindestens die Tiefe log(N).

vollständiger Baum [1] 2d+1 Knoten 2d Blätter

Im Fall des Sortierens von n Elementen gilt, dass es N = n! mögliche Permutation gibt. Ein Baum mit n! Blättern hat mindestens die Tiefe log(n!). Im obigen Beispiel für n=3 gilt 3! = 1*2*3 = 6 und damit für die Tiefe d

<math>d = \lceil \log_2(6)\rceil \approx \lceil 2.6\rceil = 3</math>

Im ungünstigsten Fall braucht man bei dem Frage-Baum drei Schritte. Weil aber <math>\log(6)\approx 2.6 < 3</math> muss nicht jeder Pfad zu Ende durchlaufen werden, um die Lösung zu bekommen.

Allgemein gilt

<math>d \ge \log_2(n!) = \log_2(1\cdot 2\cdot ... \cdot n) = \log_2(1) + \log_2(2) + ... + \log_2(n) = \sum_{k=1}^n \log_2(k) = \frac{1}{\ln(2)}\sum_{k=1}^n \ln(k) = \frac{1}{\ln(2)}\sum_{k=2}^n \ln(k)</math>

Die letzte Identität gilt, weil <math>\ln(1) = 0</math> in der Summe weggelassen werden kann. Eine untere Schranke für die Tiefe kann man explizit bestimmen durch die Methode der

Abschätzung von Summen durch Integrale

Gegeben sei eine monoton wachsende Funktion f(x) (blaue Kurve). Das bestimmte Integral über die Funktion sei

<math>\int_{x_1}^{x_2} f(x)dx</math>.

Wenn wir das Funktionsargument x abrunden (schwarze Kurve), entsteht ein Integral, das einen kleineren Wert als das ursprüngliche Integral hat. Runden wir auf (rote Kurve), entsteht ein Integral mit einem größeren Wert:

<math>\int_{x_1}^{x_2} f(\lfloor x \rfloor)dx \le \int_{x_1}^{x_2} f(x)dx \le \int_{x_1}^{x_2} f(\lceil x \rceil)dx</math>

In unserem Zusammenhang sind x₁ und x₂ positive ganze Zahlen. Deshalb gilt

<math>f(\lfloor x \rfloor)_{x_1}^{x_1+1}= f(x_1),</math>

<math>f(\lfloor x \rfloor)_{x_1+1}^{x_1+2}= f(x_1+1)</math>

<math>...</math>

<math>f(\lfloor x \rfloor)_{x_2-1}^{x_2}= f(x_2-1)</math>

Wir können die obigen Integrale daher folgendermaßen vereinfachen:

<math>\begin{array}{lcl}

\int_{x_1}^{x_2} f(\lfloor x \rfloor) dx &=& \int_{x_1}^{x_1 + 1} f(\lfloor x \rfloor) dx + ...+ \int_{x_2-1}^{x_2} f(\lfloor x \rfloor) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2-1) dx \\ & = & f(x_1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2-1) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1) + ...+ f(x_2-1) \\ & = & \sum_{k=x_1}^{x_2-1} f(k) \end{array}</math> für die Fläche unter den schwarzen Rechtecken sowie

<math>\begin{array}{lcl}

\int_{x_1}^{x_2} f(\lceil x \rceil) dx &=& \int_{x_1}^{x_1 + 1} f(\lceil x \rceil) dx + ...+ \int_{x_2-1}^{x_2} f(\lceil x \rceil) dx \\ & = & \int_{x_1}^{x_1 + 1} f(x_1+1) dx + ...+ \int_{x_2-1}^{x_2} f(x_2) dx \\ & = & f(x_1+1) \int_{x_1}^{x_1 + 1} dx + ...+ f(x_2) \int_{x_2-1}^{x_2} dx \\ & = & f(x_1+1) + ...+ f(x_2) \\ & = & \sum_{k=x_1+1}^{x_2} f(k) \end{array}</math> für die Fläche unter den roten Rechtecken. Zusammenfassend gilt also <math> \sum_{k=x_1}^{x_2-1} f(k) \le \int_{x_1}^{x_2} f(x)dx</math> und <math> \sum_{k=x_1+1}^{x_2} f(k) \ge \int_{x_1}^{x_2} f(x)dx</math> Für unser Problem setzen wir f(k) = ln(k), x₁+1 = 2, und x₂ = n. Also können wir abschätzen

<math>\sum_{k=x_1+1}^{x_2} f(k) = \frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \ge \frac{1}{\ln(2)}\int_1^n \ln(x) dx</math>

Das Integral ist leicht zu lösen, und wir erhalten

<math>\frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \ge \frac{1}{\ln(2)}\left[x\ln(x)-x\right]_{x=1}^{n} = \frac{1}{\ln(2)}(n\ln(n)-n+1)=n\log_2(n) - \frac{n-1}{\ln(2)} \in \Omega(n \log(n))</math>

Folglich gilt:

<math>d\ge\log_2(n!) = \frac{1}{\ln(2)}\sum_{k=2}^{n} \ln(k) \in \Omega(n \log(n))</math>

Mit anderen Worten: Kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymptotisch schneller als Mergesort, denn die Anzahl der Vergleiche (= Tiefe des Entscheidungsbaumes) ist <math>\Omega(n \log(n))</math>. Falls man einen schnelleren Sortieralgorithmus benötigt, muss man ein anderes algorithmisches Prinzip verwenden, siehe dazu Übungsaufgabe 6.2.

Bucket Prinzip

Mit dem Bucket Prinzip verteilt man die Schlüssel geschickt auf die "Fächer" (buckets) und arbeitet dann mit jedem Bucket einzeln.

1) Die Schlüssel sind bereits ganze Zahlen von [0, M)

  def integerSort(a, M):
     buckets = [[] for k in xrange(M)]          #leere buckets
     for k in xrange(len(a)):
        b[a[k].key].append(a[k]) 		#verteilen
     i = 0
     for k in xrange(M):
        a[i : i+len(b[k])] = b[k]
        i += len(b[k])

2) Schlüssel sind keine integer

-> umwandeln in [0, M)

- entweder Ordnung erhalten key1 <= key2

bucketMap(key1) <= bucketMap(key2)

-> "Quantisierung"

- oder Ordnung nicht erhalten

-> "Hashing"

Bucket Sort

Bucket Sort sortiert die keys in die buckets.

  def bucketSort(a, bucketMap, c):
     M = int(c * len(a))
     b = [[] for k in xrange(M)]
     for k in xrange(len(a)):
        index = bucketMap(a[k].key, M)
        b[index].append(a[k])
     i = 0
     for k in xrange(M):
        insertionSort(b[k])
        a[i : i + len(b[k])] = b[k]
        i+= len(b[k])

Beispiel: keys sind reelle Zahlen in [0, 1)

  def bucketMap(key, M):
     return int(key + M)

Nächstes Thema