Prioritätswarteschlangen
Definitionen
Prioritätswarteschlangen verwendet man, wenn man in einem Container wiederholt das jeweils kleinste (Min Priority Queue) oder größte (Max Priority Queue) Element finden und gewöhnlich auch aus dem Container entfernen muss. Die typische Schnittstelle einer Prioritätswarteschlange pq enthält also typischerweise folgende effizient implementierte Operationen:
- Max Priority Queue
pq.insert(x) # Element x einfügen x = pq.largest() # das aktuell größte Element zurückgeben (aber es bleibt in der Queue) pq.removeLargest() # das aktuell größte Element entfernen
- Min Priority Queue
pq.insert(x) # Element x einfügen x = pq.smallest() # das aktuell kleinste Element zurückgeben (aber es bleibt in der Queue) pq.removeSmallest() # das aktuell kleinste Element entfernen
Die Funktionen insert und remove werden auch oft mit push bzw. pop bezeichnet (wie beim Stack). In vielen Implementationen gibt remove außerdem das aktuelle größte bzw. kleinste Element zurück. Neben Min und Max Queue gibt es auch die Min-Max Priority Queue (bidirektionale Prioritätswarteschlange), die das kleinste und das größte Element effizient finden und entfernen kann.
Prioritätswarteschlange als sequentielles Suchproblem
Am einfachsten kann eine Prioritätswarteschlange durch sequentielle Suche realisiert werden. In diesem Fall ist einfach ein (unsortiertes) dynamisches Array a gegeben, dessen Elemente mit Prioritäten ausgestattet sind. Dann gilt
pq.insert(x)<=> a.append(x) (amortisierte Komplexität <math>\mathcal{O}(1)</math>)
Die Suche (in diesem Fall nach dem Element mit maximaler Priorität) wird durch sequenzielles Durchlaufen des Arrays realisiert
def largest(a):
N = len(a)
if N == 0:
raise RuntimeError("Access to empty priority queue.")
max = a[0]
k = 0
for n in range(1, N): # Dieser Code entspricht der inneren Schleife von Selection Sort
if a[n] > max: # Die Suche hat also die Komplexität O(N).
max = a[n]
k = n
return k # Den Index des kleinsten Elements zurückgeben
Ähnlich implementiert man das Entfernen des größten Elements: Man sucht zunächst dessen Index, schiebt dann alle nachfolgenden Elemente um einen Index nach vorn, und verkürzt schließlich das dynamische Array um ein Element.
Alternativ kann man auch die Komplexität von insert und largest vertauschen: insert kann die Queue sortiert aufbauen (indem jedes neue Element an seinem richtigen Platz eingefügt wird, was einen Aufwand von O(N) verursacht, da man im Mittel N/2 Elemente einen Platz nach hinten verschieben muss), so dass bei largest einfach in O(1) auf das letzte Element des Array zugegriffen wird. Auch das Entfernen des größten, also letzten Elements hat jetzt die amortisierte Komplexität O(1).
Bei kleinen Arrays ist die sequentielle Suche die schnellste Methode. Bei großen Arrays hingegen ist die Suche mit O(N) nicht effizient.
Prioritätssuche mit einem binären (balancierten) Suchbaum
Ein binärer Suchbaum eignet sich offensichtlich für die Prioritätssuche, weil das Einfügen und Entfernen eines Elements sowie die Suche nach dem kleinsten oder größten Element jeweils in <math>\mathcal{O}(\log N)</math> realisiert werden kann, falls der Baum balanciert ist. Man implementiert also insert z.B. wie beim Andersson-Baum. Die Suche nach dem größten Element wird durch eine einfache rekursive Funktion realisiert:
def largest(node): # node istr die Wurzel des zu durchsuchenden Teilbaums
if node.right is not None: # rechts stehen immer die großen Elemente
return largest(node.right) # => Rekursion in den rechten Teilbaum
return node # wenn es nicht mehr nach rechts geht, dann haben wir den größten Knoten gefunden
Diese Funktion hat, wie auch insert und remove, die Komplexität <math>\mathcal{O}(\log N)</math>. Alle Funktionen sind somit für große Datenstrukturen effizient. Allerdings stellt sich heraus, dass die Datenstruktur eines balancierten Suchbaums viel komplizierter ist, als für die Prioritätssuche notwendig wäre.
Heap
Die Datenstruktur des Heap ist speziell für die Prioritätssuche optimiert. Im Unterschied zum Suchbaum sucht man ja nicht nach einem beliebigen Element, sondern stets nach dem größten oder kleinsten. Dadurch kann die Datenstruktur signifikant vereinfacht werden.
Linkslastiger perfekt-balancierter Binärbaum
Ein linkslastiger Binärbaum ist ein Binärbaum, bei dem für jeden Knoten gilt, dass die Tiefe des linken Unterbaumes größer oder gleich der Tiefe des rechten Unterbaumes ist. Ein leerer Unterbaum hat dabei die Tiefe Null.
- d(node.left) ≥ d(node.right)
Wenn ein linkslastiger Binärbaum außerdem perfekt balanciert ist, gilt für alle Knoten sogar
- 1 ≥ d(node.left) - d(node.right) ≥ 0
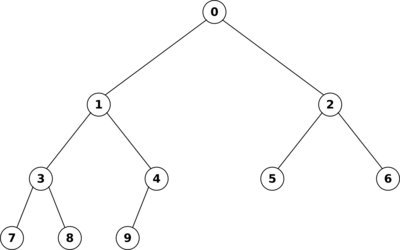
d.h., die Höhe des linken Teilbaums kann maximal um Eins größer sein als die des rechten. Die folgende Graphik zeigt, dass man einen linkslastigen, perfekt balancierter Binärbaum effizient als Array implementieren kann, indem man die Knoten von oben nach unten und von rechts nach links durchnummeriert, und diese Nummern als Array-Indizes verwendet:
Dieser Baum entspricht dem Array
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
In der Array-Repräsentation kann man den Vater und die Kinder eines gegebenen Knotens index durch einfache Umrechnung der Arrayindizes bestimmen:
parentIndex = ⌊(index - 1)/2⌋ # ⌊.⌋ heißt abrunden leftChildIndex = 2*index + 1 rightChildIndex = 2*index + 2
Diese Formeln gelten unter der Voraussetzung, dass die Indexzählung bei Null beginnt. Die Wurzel des Baumes hat also den Index 0. Ein neuer Knoten wird einfach am Ende des Arrays angehängt, und er ist ein linkes Kind, falls sein Index ungerade ist, andernfalls ein rechtes Kind. Offensichtlich bleibt durch diese Einfügestrategie die Eigenschaften der Linkslastigkeit und perfekten Balance erhalten.
Heap-Bedingung
Ein Heap ist ein linkslastiger perfekt-balancierter Binärbaum, für den zusätzlich eine Heap-Bedingung gilt. Ein Baum erfüllt die Max-Heap-Bedingung, wenn für jedem Teilbaum gilt, dass die Wurzel eine höhere Prioriät hat als die Kinder. Entsprechend erfüllt der Baum die Min-Heap-Bedingung, wenn die Wurzel kleinere Priorität hat als die Kinder.
Im Kontext der array-basierten Repräsentation bedeutet dies, dass die Wurzel, also das Element heap[0] die größte (bzw. kleinste) Priorität hat. Die Funktion largest kann somit trivial implementiert werden:
def largest(heap):
return heap[0] # Komplexität <math>\mathcal{O}(1)</math>
Einfügen und Löschen bei einem Heap
Bei Einfügen in einem Heap müssen wir sicherstellen, dass einerseits die Heap-Bedingung erfüllt wird, und andererseits der Baum linkslastig und perfekt balanciert bleibt. Wir hatten bersits gesehen, dass letzteres immer gilt, wenn wir das neue Element einfach am Ende des Arrays anhängen. Danach rufen wir eine Hilffunktion upheap auf, die die Heap-Bedingung wieder herstellt, falls sie durch das neu eingefügte Element verletzt wird:
def insert(heap, x):
heap.append(x) # Speichern des neuen Elements am Ende (in <math>\mathcal{O}(1)</math> amortisiert) => Heap bleibt linkslastiger, perfekt balancierter Baum
upheap(heap, len(heap)-1) # repariere die Heap-Bedingung für Element len(heap)-1 (also das gerade eingefügte Element)
Die Funktion upheap prüft, dass der Vaterknoten höhere (Max-Heap) bzw. niedrigere (Min-Heap) Priorität hat als der neue Knoten. Ist dies nicht der Fall, werden die beiden Knoten getauscht, und die Überprüfung wird rekursiv auf den Vaterknoten angewendet. Während der Reparaturen wandert man also im Baum aufwärts Richtung Wurzel, daher der Name der Funktion:
def upheap(heap, k):
"""das k-te Element ist evtl. im Heap zu tief einsortiert und erfüllt die Heap-Bedingung nicht"""
v = heap[k] # k-tes Element zwischenspeichern
while True: # Endlosschleife wird unten durch break verlassen
if k == 0: # wir sind an der Wurzel
break # => Heap-Bedingung ist auf jeden Fall erfüllt
parent = (k - 1)/2 # Berechnung der Vaterindex (automatisches Abrunden wegen Integer-Division)
if heap[parent] > v: # wenn die Max-Heap-Bedingung erfüllt ist
break # => Abbruch der Rekursion
heap[k] = heap[parent] # sonst: parent-Element muss eine Ebene nach unten verschoben werden
k = parent # und parent wird der neue Index k
heap[k] = v # heap[k] ist jetzt die richtige Stelle für das neue Element
Die Anzahl der Schleifendurchläufe entspricht maximal der Tiefe des Baumes. Die Komplexität von insert ist somit <math>\mathcal{O}(\log N)</math>, weil der Baum balanciert ist.
Bei removeLargest müssen wir entsprechend das erste Element heap[0] aus dem Array entfernen. Allerdings kann aus einem dynamischen Array nur das letzte Element effizient (in amortisiert O(1)) entfernt werden. Wir verwenden deshalb einen Trick: Wir überschreiben das Element heap[0] mit dem letzten Element heap[-1], und löschen dann das letzte Element (das ja jetzt zweimal im Heap ist). Da das letzte Element normalerweise nicht das Element mit der größten Priorität sein wird, muss mit der Hilfsfunktion downHeap noch die Heap-Bedingung repariert werden.
def removeLargest(heap):
heap[0] = heap[-1] # das letzte Element auf die erste Stelle bringen (das bisherige erste Element ist damit gelöscht)
del heap[-1] # das letzte Element löschen <math>\mathcal{O}(1)</math>
downHeap(heap, 0) # repariere die Heap-Bedingung für Element 0
Die Funktion downHeap geht jetzt im Baum abwärts in Richtung der Blätter und stellt sicher, dass die Kinder jedes Knotens kleinere Prioritäten haben als der Knoten selbst:
def downHeap(heap, k):
"""das k-te Element ist evtl. im Heap zu hoch einsortiert und erfüllt die Heap-Bedingung nicht"""
v = heap[k] # k-tes Element zwischenspeichern
while True: # Endlosschleife wird unten durch break verlassen
child = 2*k + 1 # linkes Kind
if child >= len(heap): # Kind existiert nicht (k ist Blattknoten)
break # => Rekursion abbrechen
if child + 1 < len(heap) and heap[child] < heap[child + 1] # rechtes Kind existiert und ist größer
child = child + 1 # => vergleiche mit rechtem Kind (sonst mit linkem)
if v >= heap[child]: # wenn die Max-Heap-Bedingung erfüllt ist
break # => Abbruch der Rekursion
heap[k] = heap[child] # sonst: child-Element muss eine Ebene nach oben verschoben werden
k = child # und child wird der neue Index k
heap[k] = v # heap[k] ist jetzt die richtige Stelle für das Element v
Auch in dieser Funktion erreicht die Anzahl der Schleifendurchläufe maximal die Tiefe des Baumes. removeLargest hat somit eine Komplexität von <math>\mathcal{O}(\log N)</math>.
Beispiel am Wort "SORTING"
Wir fügen die Buchstaben [S, O, R, T, I, N, G] in dieser Reihenfolge in eine Max Priority Queue ein. Bei den ersten drei Buchstaben passiert nichts interessantes, da S der größte von ihnen ist und somit die Heap-Bedingung nicht verletzt wird. Wir bekommen also den Heap:
S | \ | \ O R
(um das Ganze anschaulicher zu machen, verwenden wir die Baumdarstellung des Heap anstelle der Array-Darstellung). Fügt man jetzt T am Ende des Heap ein, wird es zum linken Kind von O, und die Heap-Bedingung ist verletzt. Wir benötigen zwei Iterationen von upheap, um die Heap-Bedingung wieder herzustellen:
S S T | \ | \ | \ | \ | \ | \ O R => T R => S R | | | T O O
Beim Einfügen von I, N und G am Ende des Heaps wird die Heap-Bedingung nicht verletzt:
T | \ | \ S R |\ |\ O I N G
Entfernen wir jetzt das größte Element T, wird zuerst das letzte Element (also G) an die Position 0 gebracht. Die Heap-Bedingung muss jetzt durch zwei Iterationen von downHeap repariert werden:
G S S | \ | \ | \ | \ | \ | \ S R => G R => O R |\ | |\ | |\ | O I N O I N G I N
Beim Entfernen von S kommt N an die Position 0. Hier genügt eine Iteration, um die Heap-Bedingung wieder herzustellen:
N R | \ | \ | \ | \ O R => O N |\ |\ G I G I
Der nächste Aufruf von removeLargest bringt das I an Position 0, und es wird ein Schritt zur Reparatur benötigt:
I O | \ | \ | \ | \ O N => I N | | G G
Weitere Heapvarianten
- Min-Max-Priority Queue ("Deap", Double Ended Heap): Implementiert largest, smallest, reamoveLargest, removeSmallest jeweils in <math>\mathcal{O}(\log N)</math>.
- Binomialer Heap: Erlaubt das effiziente Zusammenführen zweier Prioritätslisten. Fügt eine effiziente Operation "mergeHeaps" hinzu, die aus zwei gegebenen Heaps mit N1 und N2 in <math>\mathcal{O}(\log N)</math> einen neuen Heap mit N=N1+N2 Elementen erzeugt. Der Name der Datenstruktur leitet sich von den Binomialkoeffizienten her, die in den Beweisen der Eigenschaften benutzt werden.
- Fibonacci-Heap: Einfügen und Entfernen erfolgen in amortisiert konstanter Zeit <math>\mathcal{O}(1)</math>. Der Name kommt von den Fibonacci-Zahlen, die in den Beweisen benutzt werden.