Hashing und assoziative Arrays

Mitschrift gibts hier als PDF und hier gibts die TeX-Sourcen, leider als PDF weil man wohl keine .TeXs hochladen darf. Originale gibts auf Anfrage bei kirchner at cl dot uni minus heidelberg dot de. Wird das Package "listings" verwendet, das gibts bei http://tug.ctan.org/tex-archive/macros/latex/contrib/listings/

Tipp- und sonstige Fehler dürfen gerne verbessert und erneut hochgeladen werden, oder gebt mir per Email Bescheid, dann pflege ich die Korrektur ein :)

Ich Finde dein Aufschrieb sollte ins Wiki übetragen werden, das bietet auch alles, was du mit Latex machen kannst. Die Bäume kannst du z.B. mit Latex zeichnen, einen pro Seite und diese dann in eine png Datei umwandeln. Wie sowas geht kann man z.B. in den Quellen von doxygen oder mediawiki selbst nachlesen. Oder man zoomt rein und macht einen Screenshot :-)

Assotiative Arrays

• ähnlich Arrays X = a[i], a[i] = x, wobei der Typ von i beliebig sein kann (beim Array gilt <math> i \in 0 \ldots N-1</math>)
• z.B. Wörterbuch x = toEnglish[word], typ[word] == string, (word ist in diesem Fall i, außerdem ist ein String als Index einer der häufigsten Fälle)

offensichtliche Realisierung

zurückführen auf Suchen. Die Datenstruktur muss also erweitert so werden, dass mehr Informationen gespeichert werden können, z.B. durch eine erweiterte Node-Klasse um Feld "data" node: key, node: data

Verwende sequentielle Suche oder Baumsuche um die beiden Zugriffsoperatoren zu implementieren: a[i] mit sequentieller Suche <math> a[i] \in O(n)</math> mit Baumsuche <math> a[i] \in O(log n)</math>

• Beispiel: Die std-map wird mit Baumsuche realisiert

Nun stellt sich die Frage, ob das auch schneller, möglicherweise sogar in <math> O(1) </math> geht:

Die Antwort lautet: Ja, mit einer Hashtablle bzw. Hashing

Hashing

• gegeben: ein Schlüssel aus dem Universum U, wobei U die Menge von allem was als Schlüssel legal ist darstellt
• Hashfunktion: <math> f: u \rightarrow 0 \ldots M -1 \subset N </math>
• Definition einer Kollision wenn <math> f(u_1 \in U) = f(u_2 \in U) </math> d.h. wenn zwei Schlüssel auf die selbe Zahl Zeigen. Außerdem sind Kollisionen unvermeidlich, wenn <math> |U| > M </math> (Müsste es hier nicht < heißen?)

Aufgabe: Hash-Funktion entwerfen, die möglichst wenige Kollisionen erzeugt Hashfunktion ähnlich eines Zufallszahlengenerators, jede <math> k \in 0 \ldots M-1 </math> soll mit gleicher Wahrscheinlichekeit herauskommen (=uniformes Hashing)

Aber: für jede Hashfunktion gibt es ungünstige Konstellationen (<math> U_f \subset U f(U_f)) </math> hat viele Kollisionen. Veranschaulicht heißt das: Wenn man eine Party veranstaltet, zu der nur Leute eingeladen werden, die an einem 8ten im Monat Geburtstag haben, dann ist es viel wahrscheinlich, Leute zu finden, die am selben (oder gleichen) Tag Geburtstag haben, als wenn man alle einlädt.

D.h. die Wahl einer guten Hashfunktion ist eine Kunst und man muss die Daten analysieren um ein gutes f zu finden

Kennt man die erlaubten Schlüssel schon (<math>U_f \subset U</math>) und nur <math>U_f</math> kommt vor erhält man eine perfekte Hashfunktion ohne Kollisionen

Beispiel: Monatsnamen U ist Strings der Länge 09 -> <math>30^{9}</math> Möglichkeiten, benutzt werden 12 <math>U_f</math> = {"Januar"; "Februar"; ... ; "Dezember"}

• Hashfunktion: Anfangsbuchstabe des Monatsnamen 5bit -> M = 32 -> J, F, M, A, M, J, J, A, S, O, N, D

Dabei enstehen viele Kollisionen (J 3x, M 2x, A 2x etc.), es ist also keine gute Hashfunktion

• Hashfunktion: erste 3 Buchstaben -> 15bit -> M = <math>2^{15}</math>

-> Jan, Feb, März, Apr, Mai, Jun, Jul, Aug, Sep, Okt, Nov, Dez -> keine Kollision aber M ist groß

Die Aufgabe wird also präzisiert: die minimale, perfekte Hashfunktion wird gesucht <math> |U_f| = M </math>

• universelles Hashing: wähle die Hashfunktion per Zufallszahl -> Wahrscheinlichkeit, dass die Funktion für die Schlüssel ungünstig ist, wird minimiert
• cryptographische Hashfunktionen: (z.B. md5, sha1, ...) unter anderem für Verschlüsselung bzw. verschlüsselte Kommunikation

-> Anforderung:

• Kollision sehr unwahrscheinlich
• Hash darf nicht umkehrbar sein

aus beidem folgt, dass M sehr groß wird. So z.B. <math>M^{128}</math>

beliebte Hashfunktionen:

• Assotiatives Array M mit festgelegter Größe des Arrays

<math> f(U) = f'(U) \% M \Rightarrow \in 0\ldots M-1 </math> <math> f'(U)</math> falls

• U unsigned int(32bit int Datentyp) -> f'(U) = U
• U signed int -> |U| oder Typkonvertierung (unsigned int) U

• Andere Schlüsseltypen interpretiert man als Array of byte f'(U) konvertiert Array fo Byte -> unsigned int

beliebte Beispiele:

• Bernsteinfunktion

 def bHash(u):    #U: Array of Byte
   h=0
   for k in U:
     h = 33 * h + k  (müsste vll. eher h = heißen, hatte mir k = aufgeschrieben)
   return h

• modifizierte Bernsteinfunktion:

 def bHash(u):    #U: Array of Byte
   h=0
   for k in U:
     h = 33 * h ^ k  (^ ist bitweises Xor)
   return h

• Shift-Add-Xor-Funktion:

 def saxhash(u):
   h=0
   for k in u:
     h ^= (h << 5) + (h >> 2) + k
   return h

• Fowler/Noll/Vo-Funktion:

 def FNVhash(u):
   h = 2166136261
   for k in u:
     h = (h * 16777619) ^ k
   return h

(...)

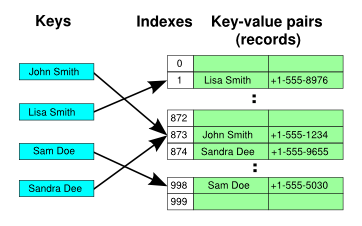
Hash-Tabelle

Kollisionen unvermeidlich, wenn Schlüssel unbekannt

• besteht aus einer Hashfunktion und einem Array der Größe M
• insert (naiv):

 def insert(u):
    index = hash(u) % M
    array[index] = u

das funktioniert allerdings nicht gar so einfach, weil eine Kollision zum überschreiben führt. Um die Kollision geschickt zu behandeln gibt es zwei Ansätze:

• lineare Verkettung
• offene Adressierung

lineare Verkettung

Das Array der Hashtabelle ist ein Array von Listen, wodurch jedes Arrayfeld beliebig viele Elemente speichern kann

 def instert(u):
   index = hash(u)%M
   array[index].append(u)   

(Laufzeit bis hier <math> O (1)</math>)

 def get(u):
   index = hash(u) % M # <math> O(1)</math>
   k = sequentialsearch(array[index],u) # <math> O(\alpha) </math> -> zusammen <math> 0 ( 1 + \alpha) </math>
   if k == -1:
     return None
   else:
     return array[index][k]

Füllstand <math> \alpha = \frac{N}{M}</math> wobei N die Größte der Hashtabelle und M die Größe des Arrays ist

Wenn alles klappt ist bei uniformen hashing die Länge der Listen <math> O ( \alpha ) </math> bei gleichmäßiger Verteilung sind alle Listen <math> \frac{N}{M} lang</math>

Beispiel: C++ std.hashmap

Hashtabelle mit linearer Verkettung

Prinzip (Quelle)

Pessimistischer Ansatz: Kollisionen treten häufig auf, deshalb wird unter jedem Hashindex gleich eine Liste angelegt, in der Einträge aufgenommen werden können.

Implementation in Python

HashNode ist eine Hilfsdatenstruktur, die Schlüssel und Wert speichert und mit Hilfe von next eine verkettete Liste realisiert

 class HashNode:
     def __init__(self,key,data,next):
         self.key = key
         self.data = data
         self.next = next # Verkettung!

Die eigentliche Hashtabelle wird in der Klasse HashTable implementiert:

 class HashTable:
     def __init__(self):
        self.capacity = ... # Geeignete Werte siehe unten
        self.size = 0
        self.array = [None]*self.capacity

In Python (Python Docs zum Thema) wird der Zugriffsoperator [ ] für eine Datenstruktur wie folgt (innerhalb einer Klasse) implementiert:

 def __setitem__(self, key, value)

so dass im Programmtext dann folgende Syntax möglich ist: a[key] = value (schreibender Zugriff auf a[key]). Analog wird der lesende Zugriff value = a[key] wie folgt umgesetzt:

 def __getitem__(self, key, value)

Implementierung der __setitem__-Funktion in der HashTable-Klasse:

 def __setitem__(self, key, value):
     index = hash(key) % self.capacity
     node = self.array[index]
     while node is not None:
         if node.key == key:
             # Element key ist schon in der Tabelle
             #Überschreibe die Daten mit dem neuen Wert
             node.data = value
             return
         # Kollision des Hashwerts, probiere nächsten Key aus
         node = node.next
     # Kein Element hatte den richtigen Schlüssel.
     # ==>Es gibt diesen Schlüssel noch nicht
     # Füge also ein neues Element in die Hashtabelle ein
      
     self.array[index] = HashNode(key, value, self.array[index])
     # Der alte Anfang der Liste wurde der Nachfolger des neu eingefügten
     # ersten Elements
      
     self.size += 1

Und die Implementierung der __getitem__ Funktionen:

 def __getitem__(self, key):
     index = hash(key) % self.capacity
     node = self.array[index]
     while node is not None:
          if node.key == key: # Gefunden!
              return node.data
          node = node.next
     raise KeyError(key)

Wahl der Kapazität

In der C++ Standardbibliothek (Klasse std::hash_map) wird die Hashtabelle häufig mit Hilfe der linearen Verkettung implementiert. Dabei wird capacity immer als Primzahl gewählt, wobei sich aufeinanderfolgende Kapazitäten immer ungefähr verdoppeln:

 53, 97, 193, 398, 769, ...

GCC hashtable.cc (Primzahlen) GCC Hash Implementation

Das hat zur Folge, dass hash(key) % self.capacity alle Bits von h benutzt (Eigenschaft aus der Zahlentheorie). Die Kapizität wird vergrößert, wenn size == capacity erreicht wird. Analog zum dynamischen Array werden die Daten dann aus dem alten Array (self.array) in ein entsprechend vergrößertes neues Array kopiert.

Hashtabelle mit offener Adressierung (offenes Hashing)

Prinzip (Quelle)

Wikipedia (de) Wikipedia (en)

Optimistischer Ansatz: Kollisionen werden nicht so häufig auftreten.

Idee

Wenn array[index] durch Kollision bereits vergeben ist, probiere einen anderen Index aus.

• Das Array enthält pro Element höchstens ein (key,value)-Paar
• Das Array muss stets mindestens einen freien Platz haben (sonst gäbe es beim Ausprobieren anderer Indizes eine Endlosschleife). Es gilt immer self.size < self.capacity. Dies war bei der vorigen Hash-Implementation mit linearer Verkettung nicht notwendig (aber im Sinne schneller zugriffszeiten trotzdem wünschenswert).

Vorgehen bei Kollisionen

Sequentielles Sondieren

Probiere den nächsten Index: index = (index+1) % capacity

• Vorteil: einfach
• Nachteil: Clusterbildung

Clusterbildung heißt, dass sich größere zusammenhängende Bereiche bilden die belegt sind, unterbrochen von Bereichen die komplett frei sind. Beim Versuche des Einfügens eines Elements an einen Platz, der schon belegt ist, muss jetzt das ganze Cluster sequentiell durchlaufen werden, bis ein freier Platz gefunden wird. Damit entspricht die Komplexität der Suche der mittleren Länge der belegten Bereiche, was sich entsprechend in einer langsamen Suche widerspiegelt.

Doppeltes Hashing

Wikipedia (de) Wikipedia (en)

Bestimme einen neuen Index (bei Kollisionen) durch eine 2. Hashfunktion.

Das doppelte Hashing wird typischerweise in der Praxis angewendet und liegt auch der Python Implementierung des Datentyps Dictionary (Syntax {'a':1, 'b':2, 'c':3} zugrunde.

Eine effiziente Implementierung dieses Datentyps ist für die Performance der Skriptsprache Python extrem wichtig, da z.B. beim Aufruf einer Funktion der auszuführunde Code in einem Dictionary unter dem Schlüssel Funktionsname nachgeschlagen wird oder die Werte lokaler Variablen innerhalb einer Funktion ebenfalls in einem Dictionary zu finden sind.

Für die Implementierung in Python werden wieder die obigen Klassen HashNode (das Attribut next kann allerdings jetzt entfernt werden) und HashTable benötigt, es folgen die angepassten Implementationen von __setitem__ und __getitem__:

 def __setitem__(self, key, value):
     h = hash(key)
     index = h % self.capacity
     while True:
         if self.array[index] is None or self.array[index].key is None:
              # das Feld ist frei (1. Abfrage)
              # oder das Feld ist als frei markiert (2. Abfrage)
              self.array[index] = HashNode(key, value)
              self.size +=1
              return
         if self.array[index].key == key:
              # Es gibt diesen Schlüssel schon,
              # überschreibe die Daten
              self.array[index].data = value
              return
         # Letzter Fall: Kollision => neuer Index durch 2. Hashfunktion
         index = (5*index+1+h) % self.capacity
         h = h >> 5

(für den >>-Operator, siehe die Python Dokumentation)

Die vorgestellte Implementierung orientiert sich an Pythons interner Dictionary Implementierung, der zugehörige Quelltext (mit ausführlichem Kommentar) findet sich unter dictobject.c Python Implementation (SVN)

Beispiel

Mit Zahlen <math>2^5</math> statt <math>2^{32}</math>.

 h=25, capacity=8
 i_0 = 25%8 = 1
 Es finde eine Kollision statt.
 i_1 = (5*1+h)%8 = 31%8 = 7
 h = h>>2 <==> h = (0b11001)>>2 = 0b00110 = 6
 Es finde eine Kollision statt.
 i_2 = (5*7+1+h)%8  =42%8 = 2
 h = h>>2 <==> h=1
 Es finde eine Kollision statt.
 i_3 = (5*2+1+h)%8 = 12%8 = 4
 h = h>>2 <==> h=0
 Es finde eine Kollision statt.
 i_4 = (5*4+1+0)%8 = 5
 i_5 = (5*5+1)%8 = 2
 i_6 = (5*2+1)%8 = 3
  ...

Allen Indizes werden erreicht bevor sich die Folge wiederholt.

Komplexität des offenen Hashings

• Annahme: uniformes Hashing, das heißt alle Indizes haben gleiche Wahrscheinlichkeit
• Füllstand <math>\alpha = \frac{\text{size}}{\text{capacity}}</math>

• Erfolglose Suche (d.h. es wird entweder ein neues Element eingefügt oder ein KeyError geworfen): Untere Schranke für die Komplexität ist <math>\Omega\left(\frac{1}{1-\alpha}\right)</math> Schritte (= Anzahl der notwendigen index-Berechnungen).
• Erfolgreiche Suche <math>\Omega\left(\frac{1}{\alpha}\ln\left(\frac{1}{1-\alpha}\right)\right)</math> Schritte.

<math>\alpha</math>	0.5	0.9
erfolglos	2.0	10
erfolgreich	1.4	2.6

Wahl der Kapazität

In Python wird capacity Aufgrund der obigen Beobachtung so gewählt, dass <math>\alpha \leq 2/3</math>. Falls <math>\alpha</math> größer werden sollte, verdopple die Kapazität und kopiere das alte array in das neue Array (analog zum dynamischen Array)

In Python werden die Kapazitätsgrößen als Zweierpotenzen gewählt, also 4,8,16,32,..., so dass h % self.capacity nur die unteren Bits von h benutzt.

Anwendung von Hashing

• Hashtabelle, assoziatives Aray
• Sortieren in linearer Zeit (Übungsaufgabe 6.2)
• Suchen von Strings in Texten: Rabin-Karp-Algorithmus
• ...

Rabin Karp Algorithmus

Wikipedia (de) Wikipedia (en)

In Textverarbeitungsanwendungen ist eine häufig benutzte Funktion die Search & Replace Funktionalität. Die Suche sollte in O(len(text)) möglich sein, aber ein naiver Algorithmus braucht O(len(text)*len(searchstring))

Naive Implementierung der Suche

 def search(text, s):
     M, N = len(text), len(s)
     for k in range(M-N):
         if s==text[k:k+N]:   # O(N), da N Zeichen verglichen werden müssen
             return k
     return -1 #nicht gefunden

Idee des Rabin Karp Algorithmus

Statt Vergleichen s==text[k:k+N], die O(N) benötigen da N Vergleiche der Buchstaben durchgeführt werden müssen, Vergleiche die Hashs von Suchstring und dem zu untersuchenden Textabschnitt: hash(s) == hash(text[k:k+N]). Dabei muss natürlich hash(s) nur einmal berechnet werden, wohingegen hash(text[k:k+N]) immer wieder neu berechnet werden muss. Damit der Vergleich O(1) sein kann, ist es deswegen erforderlich, eine solche Hashfunktion zu haben, die nicht alle Zeichen (das wäre O(N) ) einlesen muss, sondern die vorhergehende Hashfunktion mit einbezieht.

Eine solche Hashfunktion heißt Running Hash und funktioniert analog zum Sliding Mean.

Die Running Hash Funktion berechnet in O(1) den hash von text[k+1:k+1+N] ausgehend vom hash für text[k:k+N].

Idee: Interpretiere den Text als Ziffern in einer base d Darstellung:

<math>h_k = \text{text}[k]\cdot d^{N-1} + \text{text}[k]\cdot d^{N-2} + \cdots + \text{text}[k+N-1]</math>

Für die Basis 10 (Dezimalsystem) ergibt sich also

<math>h_k = \text{text}[k]\cdot {10}^{N-1} + \text{text}[k]\cdot {10}^{N-2} + \cdots + \text{text}[k+N-1]</math>

Daraus folgt

<math>h_{k+1} = 10\cdot h_k - \text{text}[k]\cdot {10}^{N} + \text{text}[k+N]</math>

Die Komplexität dieses Updates ist O(1), falls man <math>{10}^{N}</math> vorberechnet hat.

In der Realität wählt man dann d=32 und benutzt noch an einigen Stellen modulo Operationen, um die Zahlen nicht zu groß werden zu lassen.

Implementation

 def searchRabinKarp(text, s):
     ht, hs, dN = 0, 0, 1
     M, N = len(text), len(s)
     d, q = 32, 33554393
     #q ist eine große Primzahl, aber so,
     #dass d*q < 2**32 (um Überlauf zu vermeiden)
     
     #Initialisierung      
     for k in range(N):
         ht = (ht*d + ord(text[k])) % q
         #ord() gibt die ASCIInummer des übergebenen Zeichens zurück
         hs = (hs*d + ord( s[k] )) % q
         dN = (dN*d) % q
     #Die Variablen sind jetzt wie folgt initialisiert:
     #ht = hash(text[0:N])
     #hs = hash(s)
     #dN = (d**N) % q
     
     #Hauptschleife
     k = 0 
     while k < M-N:
         if hs == ht and s==text[k:k+N]:
             return k # serch string an Position k gefunden
         if k+N < M:
             ht = (d*ht - dN * ord(text[k]) + dN*q + ord(text[k+N]) ) % q
         k +=1
     return -1  # search string nicht gefunden