Prioritätswarteschlangen

* Max Priority Quene : insert(x)
                      x = largest()
                      removeLargest()

* Min Priority Quene: smallest()
                     removeSmallets()

Prioritätswarteschlange als Suchproblem

Sequentielle Suche - Array mit Prioritäten : insert(x)<=> a.append(x) ( <math>\mathcal{O}(1)</math>(amortisierte Komplexität))

def largest(a):

   if len (a) == 0:  

       raise RuntimeError("...")

    max = a[0]

    k = 0

    for n in range(1, len(a):             (innere Schleife von SelectionSort)

       if a[n] > max                       (Das ganze hat die Komplexität: N = len(a) => <math>\mathcal{O}(N)</math>

           max = a[n]

               k = n

    return k

Bei kleine Array ist dies die schnellste Methode

Binärer (balancierter)Suchbaum

insert => z.B. wie beim Anderson Baum [1] <math>\mathcal{O}(logN)</math>

def largest(node):                     # Wurzel

   if node.right is not None:    #rechts stehen immer  die großen

       return largest(node.right)

   return node                   #wenn es nicht mehr nach rechts geht, dann haben wir den größten Knoten gefunden

Das ganze hat <math>\mathcal{O}(logN)</math> Komplexität
Ergebnis: gute Komplexität aber komplizierte Datenstruktur

Heap

Datenstruktur optimiert für Prioritätssuche - man sucht nicht effizient alle Knoten, sondern nur einen bestimmten z.B. Heap max
Definition: ein linkslastiger Binärbaum ist ein Baum mit <math>d(node.left) \geq d(node.right)</math>

Ein Heap ist ein linkslastiger, perfekt balancierter Baum. (lässt sich max. um 1 unterscheiden)

Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht:

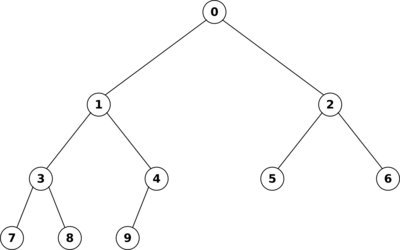
index[parent] = [(indexChild - 1)/2]   #[] heißt abgerundet

index[left] = index[parent]2 + 1

index[right] = index[parent]2 + 2

=> linkslastiger perfect balancierter Binärbaum kann effizient als Array abgespeichert werden
=>verwende Indizes wie oben

Heap - Bedingung

die Wurzel hat höhere Prioriät als die Kinder(gilt für jeden Teilbaum)

=>Wurzel = array[0] hat die größte Priorität

def largest(h):

    return h[0]        <math>\mathcal{O}(N)</math>

Einfügen in einem Heap

h - Array #speichrt Haep

 def insert(h,x):

     h.append(x)  # wir speichern den Wurzel am Ende, so wird glecih zu einem linkslastigen perfect balancierten Baum (die Haep - Bedingung ist erfüllt)

     upheap(h, len(h) - 1):

def upheap(h, k):

   """k-tes Element evtl. an der falsche Stelle

   """

   v = h[k]

   while True      #endlose Schleife
        
       if k == 0:

           break

       parent = (k - 1)/2

       if h[parent]>v:

           break

       h[k] = h.parent

       k = parent

   h[k] = v

def removeLargest(h):
    h[0] = h[len(h) - 1]

    del h[len(n) - 1]              <math>\mathcal{O}(1)</math>

    downHeap(h, 0)                       <math>\mathcal{O}(logN)</math>

def downHeap(h, k):

    v = h[k]

    while True

        child = 2k + 1              #linke Kind

        if child <math>\ge</math>len(h):

              break

        if child < and h[child] < h[child + 1]         #rechtes Kind

              child = child + 1
        if v <math>\ge</math> h[child]:

              break

        h[k] = h[child]

        k = child

   h[k] = v

Beispiel am Wort "SORTING"

(Grafiken folgen)

weitere Heapvarianten

Min-Max-Priority Queue ("Deap", Double Ended Heap)
Binomialer Heap, effiziente Operation "merege Heap" <math>\mathcal{O}(n * log N (i*N_1 + N_2)</math>

(Beweis durch binomiale Koeffizienten, Zusammenführen zweier Prioritätslisten)

Fibonacci-Heap, einfügen in amortisierter Zeit <math>\mathcal{O}(1)</math>

(Beweis durch Fibonacci Zahlen)

Prioritätswarteschlangen

Contents