Effizienz: Difference between revisions
(New page: (Vorlesung 7.5.:) == Laufzeit == Die Laufzeit ist für den Benutzer ein wichtiges Kriterium. Schwierigkeit bei der Bestimmung: Die Laufzeit hängt von vielen Faktoren ab die evtl. nicht k...) |
No edit summary |
||
| Line 84: | Line 84: | ||
* Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme. | * Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme. | ||
* Formal: Eine Funktion <math>f(x) \in O(g(x)) \!</math>* genau dann wenn es gibt eine Konstante <math>c \!</math>, so dass <math>f(x) \le cg(x), \forall x > x_0 \!</math> | * Formal: Eine Funktion <math>f(x) \in O(g(x)) \!</math>* genau dann wenn es gibt eine Konstante <math>c \!</math>, so dass <math>f(x) \le cg(x), \forall x > x_0 \!</math> | ||
=== Ein einfaches Beispiel === | |||
[[Image:Sqsqrt.png]] | [[Image:Sqsqrt.png]] | ||
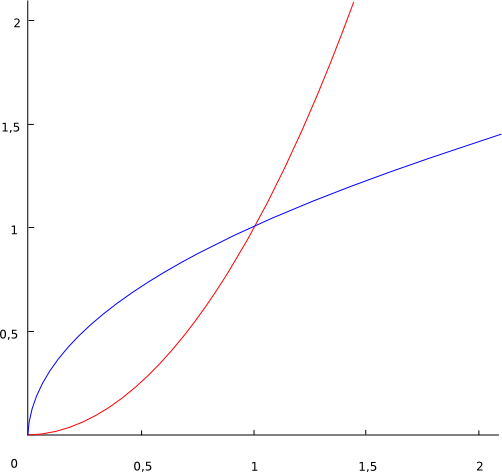
Rot = <math>x^2 \!</math> | |||
Blau = <math>\sqrt{x} \!</math> | |||
<math>\sqrt{x} \in O(x^2)\!</math> weil <math>\sqrt{x} \le x^2\!</math> für alle <math>x < x_0 = 1 \!</math> | |||
=== Komplexität bei kleinen Eingaben === | |||
Algorithmus 1: <math>O(N^2) \!</math> | |||
Algortihmus 2: <math>=O(N\log{N}) \!</math> | |||
Algorithmus 2 ist schneller (Von geringerer Komplexität), aber bei vielen wiederholten kleinen Eingaben ist Algorithmus 1 schneller. | |||
=== Eigenschaften der O-Notation(Rechenregeln) === | |||
# Transitiv: | |||
<math>f(x) \in O(g(x)) \land g(x) \in O(h(x)) \to f(x) \in O(h(x)) \!</math> | |||
# Additiv: | |||
<math>f(x) \in O(h(x)) \land g(x) \in O(h(x)) \to f(x) + g(x) \in O(h(x)) \!</math> | |||
# Für Monome gilt: | |||
<math>x^k \in O(x^k)) \land x^k \in O(x^{k+j}), \forall j \ge 0 \!</math> | |||
Revision as of 15:08, 8 May 2008
(Vorlesung 7.5.:)
Laufzeit
Die Laufzeit ist für den Benutzer ein wichtiges Kriterium. Schwierigkeit bei der Bestimmung: Die Laufzeit hängt von vielen Faktoren ab die evtl. nicht kontrollierbar sind:
- Prozessor/Auslastung des Systems
- Speicher/Cache/Bus
- Compiler/Optimierer des Compilers (Compiler auf verschiedene Architekturen optimiert?)
- Geschick des Programmierers
- Daten (Beispiel Quiclsort: Best case und worst case[Vorsortierter Input] stark unterschiedlich)
All diese Faktoren sind untereinander abhängig.
Laufzeitvergleiche sind mit Vorsicht zu interpretieren. Generell sollten bei Vergleichen möglichst wenige Parameter verändert werden, z.B.
- gleiches Programm(gleiche Kompilierung), gleiche Daten, andere Prozessoren
oder
- gleiche CPU, Daten, andere Programme (Vergleich von Algorithmen)
Beobachtung: Durch Laufzeitmessung ist schwer festzustellen, ob ein Alg prinzipiell besser ist als ein anderer.
Komplexität
Komplexitätsbetrachtungen ermöglichen den Vergleich der prinzipiellen Eigenschaften von Algorithmen unabhängig von einer Implementation, Umgebung etc.
Eine einfache Möglichkeit ist das Zählen der Aufrufe einer Schlüsseloperation. Beispiel Sortieren:
- Anzahl der Vergleiche
- Anzahl der Vertauschungen
Beispiel: Selection Sort
for i in range(len(a)-1):
max = i
for j in range(i+1, len(a)):
if a[j] < a[max]:
max = j
a[max], a[i] = a[i], a[max] # swap
- Anzahl der Vergleiche: Ein Vergleich in jedem Durchlauf der inneren Schleife. Es ergibt sich folgende Komplexität:
- Ingesamt <math>\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1}1 = \frac{N}{2} (N-1) \!</math> Vergleiche.
- Anzahl der Vertauschungen: Eine Vertauschung pro Durchlauf der äußeren Schleife:
- Insgesamt <math>N-1 \!</math> Vertauschungen
Komplexität ist in der Regel eine Funktion der Eingabegröße (Kann auch von der Art der Daten abhängen, nicht nur von der Menge, z.B. vorsortierte Daten bei Quicksort)
Fallunterscheidung: Worst und average case
- Komplexität im ungünstigsten Fall
- Komplexität im durchschnittlichen/typischen Fall
- Der typischer Fall ist oft nur schwer oder granicht festlegbar. Es werden dann Approximationen geschaffen, z.B. können alle möglichen Permutationen der Eingabe für Sortieralgorithmen als typischer Fall angenommen werden.
Exakte Formeln für Komplexität sind schwer zu gewinnen.
Beispiele aus den Übungen (Gemessene Laufzeiten für Mergesort/Selectionsort)
- Mergesort: <math>\frac{0,977x\log x}{\log 2} + 0,267x-4.39 \!</math>
- andere Lösung: <math>1140*x*log(x) - 1819*x + 6413 \!</math>
- Selectionsort: <math>\frac{1}{2}x^2 - \frac{1}{2x} - 10^{-12} \!</math>
- andere Lösung: <math>1275x^2 - 116003^x + 11111144 \!</math>
In diesen Fällen gibt es also keine offensichtlichen Lösungen (für die Frage welcher Alg besser ist). Näherung: Betrachte nur sehr große Eingaben (Meist sind alle Algorithmen schnell genug für kleine Eingaben). Dieses Vorgehen wird Asymptotische Komplexität bezeichnet (N gegen unendlich).
Asymptotische Komplexität am Beispiel Polynom
Polynom: <math>ax^2+bx+c=p\!</math>
<math>x \!</math> sei die Eingabegröße, und wir betrachten die Entwicklung von <math>p \!</math> in Abhängigkeit von <math>x \!</math>.
- <math>x=0 \!</math>
- <math>p=c \!</math>
- <math>x=1 \!</math>
- <math>p=a+b+c \!</math>
- <math>x=1000 \!</math>
- <math>p=1000000a+1000b+c \approx 1000000a\!</math>
- <math>x \to \infty \!</math>
- <math>p \approx x^2a\!</math>
Für sehr große Eingaben verlieren also b und c immer mehr an Bedeutung, so dass am Ende nur noch a für die Komplexitätsbetrachtung wichtig ist.
O-Notation
- Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme.
- Formal: Eine Funktion <math>f(x) \in O(g(x)) \!</math>* genau dann wenn es gibt eine Konstante <math>c \!</math>, so dass <math>f(x) \le cg(x), \forall x > x_0 \!</math>
Ein einfaches Beispiel
Rot = <math>x^2 \!</math> Blau = <math>\sqrt{x} \!</math>
<math>\sqrt{x} \in O(x^2)\!</math> weil <math>\sqrt{x} \le x^2\!</math> für alle <math>x < x_0 = 1 \!</math>
Komplexität bei kleinen Eingaben
Algorithmus 1: <math>O(N^2) \!</math> Algortihmus 2: <math>=O(N\log{N}) \!</math>
Algorithmus 2 ist schneller (Von geringerer Komplexität), aber bei vielen wiederholten kleinen Eingaben ist Algorithmus 1 schneller.
Eigenschaften der O-Notation(Rechenregeln)
- Transitiv:
<math>f(x) \in O(g(x)) \land g(x) \in O(h(x)) \to f(x) \in O(h(x)) \!</math>
- Additiv:
<math>f(x) \in O(h(x)) \land g(x) \in O(h(x)) \to f(x) + g(x) \in O(h(x)) \!</math>
- Für Monome gilt:
<math>x^k \in O(x^k)) \land x^k \in O(x^{k+j}), \forall j \ge 0 \!</math>