NP-Vollständigkeit

Das Problem des Handlungsreisenden

(engl.: Traveling Salesman Problem; abgekürzt: TSP)<br\> Wikipedia (de) (en)

Optimaler Reiseweg eines Handlungsreisenden(Quelle)

• Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden.
• Hierbei soll ein Handlungsreisender nacheinander n Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden.
• Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen.

gegeben: zusammenhängender, gewichteter Graph (oft vollständiger Graph)

gesucht: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\>

auch genannt: kürzester Hamiltonkreis

- durch psychologische Experimente wurde herausgefunden, dass Menschen (in 2D) ungefähr proportionale Zeit zur Anzahl der Knoten brauchen, um einen guten Pfad zu finden, der typischerweise nur <math>\lesssim 5%</math> länger als der optimale Pfad ist<br\>

vorgegeben: Startknoten (kann willkürlich gewählt werden), vollständiger Graph

=> v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger...

also <math>\frac{(v-1)!}{2}</math> mögliche Wege in einem vollständigen Graphen

• Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird.
• Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität.

Approximationsalgorithmus

Für viele Probleme in der Praxis sind keine effizienten Algorithmen bekannt (NP-schwer). Diese (z.B. TSP) werden mit Approximationsalgorithmen berechnet, die effizient berechenbar sind, aber nicht unbedingt die optimale Lösung liefern. Beispielsweise ist es relativ einfach, eine Tour zu finden, die höchstens um den Faktor zwei länger ist als die optimale Tour. Die Methode beruht darauf, dass einfach der minimale Spannbaum ermittelt wird.

Approximationsalgorithmus für TSP<br\>

• TSP für n Knoten sei durch Abstandsmatrix D = <math>(d_{ij}) 1 \le i, j \le n</math>

gegeben (vollständiger Graph mit n Knoten, <math>d_{ij}</math> = Kosten der Kante (i,j)) <br\>

gesucht: Rundreise mit minimalen Kosten. Dies ist NP-schwer!<br\>

• D erfüllt die Dreiecksungleichung <math> \Leftrightarrow d_{ij} + d_{jk} \geq d_{ik} \text{ fuer } \forall{i, j, k} \in \lbrace 1, ..., n \rbrace</math> <br\>
• Dies ist insbesondere dann erfüllt, wenn D die Abstände bezüglich einer Metrik darstellt oder D Abschluss einer beliebigen Abstandsmatrix C ist, d.h. :<math>d_{ij}</math> = Länge des kürzesten Weges (bzgl. C) von i nach j.

• Die ”Qualität”der Lösung mit einem Approximationsalgorithmus ist höchstens um einen konstanten Faktor schlechter ist als die des Optimums.

Systematisches Erzeugen aller Permutationen

• Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\>
• Trick: interpretiere jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\>
• Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst.

gegeben: zwei Wörter a, b der Länge n=len(a) bzw. m=len(b). Sei k = min(n,m) (im Spezialfall des Vergleichs von Permutationen gilt k = n = m)<br\> Mathematische Definition, wie die Wörter im Wörterbuch sortiert sind: <br\>

<math>a<b \Leftrightarrow

\begin{cases} n < m & \text{ falls fuer } 0 \le i \le k-1 \text{ gilt: } a[i] = b[i] \\ a[j] < b[j] & \text{ falls fuer } 0 \le i \le j-1 \text{ gilt: } a[i] = b[i], \text{ aber fuer ein } j<k: a[j] \ne b[j] \end{cases}</math><br\>

Algorithmus zur Erzeuguung aller Permutationen:

1. beginne mit dem kleinsten Wort bezüglich der lexikographischen Ordnung => das ist das Wort, wo a aufsteigend sortiert ist
2. definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt

Beispiel: Die folgenden Permutationen der Zahlen 1,2,3 sind lexikographisch geordnet

1 2 3    6 Permutationen, da 3! = 6
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
-----
0 1 2 Position

Die lexikographische Ordnung wird deutlicher, wenn wir statt dessen die Buchstaben a,b,c verwenden:

abc
acb
bac
bca
cab
cba

Eine Funktion, die aus einer gegebenen Permutation die in lexikographischer Ordnung nächst folgende erzeugt, kann wie folgt implementiert werden:

def next_permutation(a):
	i = len(a) -1  #letztes Element; man arbeitet sich von hinten nach vorne durch
	while True:  # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird
		if i <= 0: return False  # a ist letzte Permutation
		i -= 1
		if a[i]<a[i+1]: break
	#lexikogr. Nachfolger hat größeres a[i]
	j = len(a)
	while True:
		j -= 1
		if a[i] < a[j]: break
	a[i], a[j] = a[j], a[i] #swap a[i], a[j]
	#sortiere aufsteigend zwischen a[i] und Ende
	#zur Zeit absteigend sortiert => invertieren
	i += 1
	j = len(a) -1
	while i < j:
		a[i], a[j] = a[j], a[i]
		i += 1
		j-= 1
	return True  # eine weitere Permutation gefunden
 	
 def naiveTSP(graph):
	start = 0
	result = range(len(graph))+[start]
	rest = range(1,len(graph))
	c = pathCost(result, graph)
	while next_permutation(rest):
		r = [start]+rest+[start]
		cc = pathCost(r, graph)
		if cc < c:
			c = cc
			result = r
		return c, result

Komplexität: <math>(v-1)!</math> Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also <math>O(v!) = O(v^v)</math>

Beispiel

i = 0			j = 3
↓			↓
1	4	3	2	#input für next_permutation
	i = 2		j = 3
	↓		↓
2	4	3	1	# vertauschen der beiden Elemente
		i = 2
		j = 2
		↓
1	2	3	4	#absteigend sortiert

Stirling'sche Formel

Wikipedia (de) (en)

Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Stirling'sche Formel z.T. starke Vereinfachungen erzielen. <math>v! \approx \sqrt{2 \pi v} \left(\frac{v}{e}\right)^v</math>

<math>O(v!) = O\left(\sqrt{v}\left(\frac{v}{e}\right)^v\right) \approx O(v^v)</math>

Anwendung: Das Erfüllbarkeitsproblem in Implikationengraphen

Das Erfüllbarkeitsproblem hat auf den ersten Blick nichts mit Graphen zu tun, denn es geht um Wahrheitswerte logischer Ausdrücke. Man kann logische Ausdrücke jedoch unter bestimmten Bedingungen in eine Graphendarstellung überführen und somit das ursprüngliche Problem auf ein Problem der Graphentheorie reduzieren, für das bereits ein Lösungsverfahren bekannt ist. In diesem Abschnitt wollen wir dies für die sogenannten Implikationengraphen zeigen, ein weiteres Beispiel findet sich im Kapitel NP-Vollständigkeit.

Das Erfüllbarkeitsproblem

(vgl. WikiPedia (de))

Das Erfüllbarkeitsproblem (SAT-Problem, von satisfiability) befasst sich mit logischen (oder Booleschen) Funktionen: Gegeben sei eine Menge <math>\{x_1, ... ,x_n\}</math> Boolscher Variablen (d.h., die <math>x_i</math> können nur die Werte True oder False annehmen), sowie eine logische Formel, in der die Variablen mit den üblichen logischen Operatoren

<math>\neg\quad</math>: Negation ("nicht", in Python: not)

<math>\vee\quad</math>: Disjunktion ("oder", in Python: or)

<math>\wedge\quad</math>: Konjuktion ("und", in Python: and)

<math>\rightarrow\quad</math>: Implikation ("wenn, dann", in Python nicht als Operator definiert)

<math>\leftrightarrow\quad</math>: Äquivalenz ("genau dann, wenn", in Python: ==)

<math>\neq\quad</math>: exklusive Disjunktion ("entweder oder", in Python: !=)

verknüpft sind. Klammern definieren die Reihenfolge der Auswertung der Operationen. Für jede Belegung der Variablen <math>x_i</math> mit True oder False liefert die Formel den Wert der Funktion, der natürlich auch nur True oder False sein kann. Wenn Formel und Belegung gegeben sind, ist die Auswertung der Funktion ein sehr einfaches Problem: Man transformiert die Formel in einen Parse-Baum (siehe Übungsaufgabe "Taschenrechner) und wertet jeden Knoten mit Hilfe der üblichen Wertetabellen für logische Operatoren aus, die wir hier zur Erinnerung noch einmal angeben:

<math>a</math>	<math>b</math>	<math>a \vee b </math>	<math>a \wedge b</math>	<math>a \rightarrow b</math>	<math>b \rightarrow a</math>	<math>a \leftrightarrow b</math>	<math>a \neq b</math>
0	0	0	0	1	1	1	0
0	1	1	0	1	0	0	1
1	0	1	0	0	1	0	1
1	1	1	1	1	1	1	0

Beim Erfüllbarkeitsproblem wird die Frage umgekehrt gestellt:

Gegeben sei eine logische Funktion. Ist es möglich, dass die Funktion jemals den Wert True annimmt?

Das heisst, kann man die Variablen <math>x_i</math> so mit True oder False belegen, dass die Formel am Ende wahr ist? Im Prinzip kann man diese Frage durch erschöpfende Suche leicht beantworten, indem man die Funktion für alle <math>2^n</math> möglichen Belegungen einfach ausrechnet, aber das dauert für große n (ab ca. <math>n\ge 40</math>) viel zu lange. Erstaunlicherweise ist es aber noch niemanden gelungen, einen Algorithmus zu finden, der für beliebige logische Funktionen schneller funktioniert. Im Gegenteil wurde gezeigt, dass das Erfüllbarkeitsproblem NP-vollständig ist, so dass wahrscheinlich kein solcher Algorithmus existiert. Trotz (oder gerade wegen) seiner Schwierigkeit hat das Erfüllbarkeitsproblem viele Anwendungen gefunden, vor allem beim Testen logischer Schaltkreise ("Gibt es eine Belegung der Eingänge, so dass am Ausgang der verbotene Wert X entsteht?") und bei der Planerstellung in der künstlichen Intelligenz ("Kann man ausschließen, dass der generierte Plan Konflikte enthält?"). Es ist außerdem ein beliebtes Modellproblem für die Erforschung neuer Ideen und Algorithmen für schwierige Probleme.

Normalformen für logische Ausdrücke

Um die Beschreibung von Erfüllbarkeitsproblemen zu vereinfachen und zu vereinheitlichen, hat man verschiedene Normalformen für logische Ausdrücke eingeführt. Die wichtigste ist die Konjuktionen-Normalform (CNF - conjunctive normal form). Ein Ausdruck in Konjuktionen-Normalform ist eine UND-Verknüpfung von M Klauseln:

(CLAUSE1) <math>\wedge</math> (CLAUSE2) <math>\wedge</math> ...  <math>\wedge</math> (CLAUSEM)

Jede Klausel ist wiederum ein logischer Ausdruck, der aber sehr einfach sein muss: Er darf nur noch k Variablen enthalten, die nur mit den Operatoren NICHT und ODER verknüpft werden dürfen, z.B.

 CLAUSE1 := <math>x_1 \vee \neg x_3 \vee x_8</math>

Je nachdem, wie viele Variablen pro Klausel erlaubt sind, spricht man von k-CNF und entsprechend von einem k-SAT Problem. Es ist außerdem üblich, die Menge der Variablen und die Menge der negierten Variablen zusammen als Menge der Literale zu bezeichnen:

 LITERALS := <math>\{x_1,...,x_n\} \cup \{\neg x_1,...,\neg x_n\}</math>

Formal definiert man die k-Konjunktionen-Normalform (k-CNF) am besten durch eine Grammatik in Backus-Naur-Form:

   k_CNF    ::=  CLAUSE | k_CNF <math>\wedge</math> CLAUSE
   CLAUSE   ::= (LITERAL <math>\vee</math> ... <math>\vee</math> LITERAL)  # genau k Literale pro Klausel
   LITERAL  ::=  VARIABLE | <math>\neg</math>VARIABLE
   VARIABLE ::=  <math>x_1</math> | ... | <math>x_n</math>

Beispiele:

• 3-CNF: <math>(x_1 \vee \neg x_2 \vee x_4) \wedge (x_2 \vee x_3 \vee \neg x_4) \wedge (\neg x_1 \vee x_4 \vee \neg x_5)</math>
• 2-CNF: <math>(x_1 \vee \neg x_2) \wedge (x_3 \vee x_4)</math> ...

Gesucht ist eine Belegung der Variablen mit True und False, so dass der Ausdruck den Wert True hat. Aus den Eigenschaften der UND- und ODER-Verknüpfungen folgt, dass ein Ausdruck in k-CNF genau dann True ist, wenn jede einzelne Klausel True ist. In jeder Klausel wiederum hat man k Chancen, die Klausel True zu machen, indem man eins der Literale zu True macht. Eventuell werden dadurch aber andere Klauseln wieder zu False, was die Aufgabe so schwierig macht. Die Bedeutung der k-CNF ergibt sich aus folgendem

Satz

Jeder logische Ausdruck kann effizient nach 3-CNF transformiert werden, jedoch im allgemeinen nicht nach 2-CNF.

Man kann sich also auf Algorithmen für 3-SAT-Probleme konzentrieren, ohne dabei an Ausdrucksmächtigkeit zu verlieren.

Leider gilt der entsprechende Satz nicht für k=2: Ausdrücke in 2-CNF sind weit weniger mächtig, weil man in jeder Klausel nur noch zwei Wahlmöglichkeiten hat. Bestimmte logische Ausdrücke sind aber auch nach 2-CNF transformierbar, beispielsweise die Bedingung, dass zwei Literale u und v immer den entgegegesetzten Wert haben müssen. Dies ergibt ein Paar von ODER-Verknüpfungen:

<math>(u \leftrightarrow \neg v) \equiv (u \vee \neg v) \wedge (\neg u \vee v)</math>

Die 2-CNF hat den Vorteil, dass es effiziente Algorithmen für das 2-SAT-Problem gibt, die wir jetzt kennenlernen wollen. Es zeigt sich, dass man Ausdrücke in 2-CNF als Graphen repräsentieren kann, indem man sie zunächst in die Implikationen-Normalform (INF für implicative normal form) überführt. Die Implikationen-Normalform besteht ebenfalls aus einer Menge von Klauseln, die durch UND-Operationen verknüpft sind, aber jede Klausel ist jetzt eine Implikation. Die Grammatik der Implikationen-Normalform (INF) lautet:

   INF      ::=  CLAUSE | INF <math>\wedge</math> CLAUSE
   CLAUSE   ::= (LITERAL <math>\rightarrow</math> LITERAL)  # genau 2 Literale pro Implikation
   LITERAL  ::=  VARIABLE | <math>\neg</math>VARIABLE
   VARIABLE ::=  <math>x_1</math> | ... | <math>x_n</math>

und ein gültiger Ausdruck wäre z.B.

<math>(x_1 \to x_2) \wedge (x_2 \to \neg x_3) \wedge (x_4 \to x_3)</math>

Die Umwandlung von 2-CNF nach INF beruht auf folgender Äquivalenz, die man sich aus der obigen Wahrheitstabelle leicht herleitet:

<math>(x \vee y) \equiv (\neg x \rightarrow y) \equiv (\neg y \rightarrow x)</math>

Aus dieser Äquivalenz folgt der

Satz

Ein Ausdruck in 2-CNF kann nach INF transformiert werden, indem man jede Klausel <math>(x \vee y)</math> durch das Klauselpaar <math>(\neg x \rightarrow y) \wedge (\neg y \rightarrow x)</math> ersetzt.

Man beachte, dass man für jede ODER-Klausel des ursprünglichen Ausdrucks zwei Implikationen (eine für jede Richtung des "wenn, dann") einfügen muss, um die Symmetrie des Problems zu erhalten.

Lösung des 2-SAT-Problems mit Implikationgraphen

Jeder Ausdruck in INF kann als gerichteter Graph dargestellt werden:

1. Für jedes Literal wird ein Knoten in den Graphen eingefügt. Es gibt also für jede Variable und für ihre Negation jeweils einen Knoten, d.h. 2n Knoten insgesamt.
2. Jede Implikation ist eine gerichtete Kante.

Implikationengraphen eignen sich, um Ursache-Folge-Beziehungen oder Konflikte zwischen Aktionen auszudrücken. Beispielsweise kann man die Klausel <math>(x \rightarrow \neg y)</math> als "wenn man x tut, darf man y nicht tun" interpretieren. Ein anderes schönes Beispiel findet sich in Übung 12.

Für die Implementation eines Implikationengraphen in Python empfiehlt es sich, die Knoten geschickt zu numerieren: Ist die Variable <math>x_i</math> dem Knoten i zugeordnet, so sollte die negierte Variable <math>\neg x_i</math> dem Knoten (i+n) zugeordnet werden. Zu jedem gegebenen Knoten i findet man dann den negierten Partnerknoten j leicht durch die Formel j = (i + n ) % (2*n).

Die Aufgabe besteht jetzt darin, folgende Fragen zu beantworten:

1. Ist der durch den Implikationengraphen gegebene Ausdruck erfüllbar?
2. Finde eine geeignete Belegung der Variablen, wenn der Ausduck erfüllbar ist.

Die erste Frage beantwortet man leicht, indem man die stark zusammenhängenden Komponenten des Implikationengraphen bildet. Dann gilt folgender

Satz

Seien u und v zwei Literale, die sich in der selben stark zusammenhängenden Komponente befinden. Dann müssen u und v stets den selben Wert haben, damit der Ausdruck erfüllt sein kann.

Die Korrektheit des Satzes folgt aus der Definition der stark zusammenhängenden Komponenten: Da u und v in der selben Komponente liegen, gibt es im Implikationengraphen einen Weg <math>u \rightsquigarrow v</math> sowie einen Weg <math>v \rightsquigarrow u</math>. Wegen der Transitivität der "wenn, dann" Relation kann man die Wege zu zwei Implikationen verkürzen, die gleichzeitig gelten müssen: <math>(u \rightarrow v) \wedge (v \rightarrow u)</math> (die Verkürzung von Wegen zu direkten Kanten entspricht gerade der Bildung der transitiven Hülle für die Knoten u und v). In der obigen Wertetabelle für logische Operatoren erkennt mann, dass dies äquivalent zur Bedingung <math>(u \leftrightarrow v)</math> ist. Dies ist aber gerade die Behauptung des Satzes.

Die Erfüllbarkeit des Ausdrucks ist nun ein einfacher Spezialfall dieses Satzes.

Korrolar

Der gegebene Ausdruck ist genau dann erfüllbar, wenn die Literale <math>x_i</math> und <math>\neg x_i</math> sich für kein i in derselben stark zusammenhängenden Komponente befinden.

Setzt man nämlich im Satz <math>u = x_i</math> und <math>v = \neg x_i</math>, und beide Knoten befinden sich in der selben Komponente, dann müsste gelten <math>x_i \leftrightarrow\neg x_i</math>, was offensichtlich ein Widerspruch ist. Damit kann der Ausdruck nicht erfüllbar sein. Umgekehrt gilt, dass der Ausdruck immer erfüllbar ist, wenn <math>x_i</math> und <math>\neg x_i</math> stets in verschiedenen Komponenten liegen, weil der folgende Algorithmus von Aspvall, Plass und Tarjan in diesem Fall stets eine gültige Belegung aller Variablen liefert:

1. Bestimme die stark zusammenhängenden Komponenten und bilde den Komponentengraphen. Ordne die Knoten des Komponentengraphen (also die stark zusammenhängenden Komponenten des Originalgraphen) in topologische Sortierung an.
2. Betrachte die Komponenten in der topologischen Sortierung von hinten nach vorn und weise ihnen einen Wert nach folgenden Regeln zu (zur Erinnerung: alle Literale in der selben Komponente haben den selben Wert):
   • Wenn die Komponente noch nicht betrachtet wurde, setze ihren Wert auf True, und den Wert der komplementären Komponente (derjenigen, die die negierten Literale enthält) auf False.
   • Andernfalls, gehe zur nächsten Komponente weiter.

Der Algorithmus beruht auf der Symmetrie des Implikationengraphen: Weil Kanten immer paarweise <math>(\neg u \rightarrow v) \wedge (\neg v \rightarrow u)</math> eingefügt werden, ist der Graph schiefsymmetrisch (skew symmetric): die eine Hälfte das Graphen ist die transponierte Spiegelung der anderen Hälfte. Enthält eine stark zusammenhängende Komponente <math>C_i</math> die Knoten i1, i2, ..., so gibt es stets eine komplementäre Komponente <math>C_j = \neg C_i</math>, die die komplementären Knoten j1 = (i1 + n) % (2*n), j2 = (i2 + n) % (2*n), ... enthält. Gilt <math>C_i = \neg C_i</math> für irgendein i, so ist der Ausdruck nicht erfüllbar. Den Beweis für die Korrektheit des Algorithmus findet man im Originalartikel. Leider funktioniert dies nicht für k-SAT-Probleme mit <math>k > 2</math>.

Will man nur die Erfüllbarkeit prüfen, vereinfacht sich der Algorithmus zu:

1. Bestimme die stark zusammenhängenden Komponenten.
2. Teste für alle i = 0,...,n-1, dass Knoten i und Knoten (i+n) in unterschiedlichen Komponenten liegen.

Ist der Ausdruck erfüllbar, kann man eine gültige Belegung der Variablen jetzt mit dem randomisierten Algorithmus bestimmen, den wir im Kapitel Randomisierte Algorithmen behandeln.

Die Problemklassen P und NP

• für viele Probleme kein effizienter Algorithmus bekannt (effizient = polynomielle Komplexität

O(<math>n^p</math>), für ein beliebig großes festes D; nicht effizient: langsamer als polynomiell,

z.b. O(<math>2^N</math>))

Bsp:

• Problem des Handlungsreisenden
• Steine Bäume verallg. MST: man darf zusätzliche Punkte hinzufügen
• Clique - Problem: Clique in Graph G: maximaler vollständiger Teilgraph, trivial: 2 Kinder (gibt es eine Clique mit k Mitgliedern?)
• Integer Linear Programming <math>\hat{x}</math> = arg max <math>c^T</math>x [c,x Spaltenvektoren der Länge N]

(s.t. A*x <math>\leq</math> b [A, Matrix MxN, b Spaltenvektor von M]

x<math>\in \mathbb{N}^N, \mathbb{Z}^N</math>, {0, 1}<math>^N</math> <math>\implies</math> nicht effizient

x<math>\in \mathbb{R}^N \implies</math> effizient)

Einleitung

• Komplexitätsklasse P: Effiziente Lösung bekannt (sortieren, MST, Dijkstra)

• Komplexitätsklasse NP: Existiert ein effizienter Algorithmus um einen geratenen Lösungsvorschlag zu überprüfen.

geraten durch "Orakel" -> Black Box, nicht bekannt wie!

offensichtlich gilt P<math>\subset</math>NP (bekannter Lösungsalgorithmus kann immer als Orakel dienen). Offen ob:

-P<math>\subset</math>NP (es gibt Probleme ohne effizienten Alg)

-oder P=NP (effizienter Algorithmus nur noch nicht entdeckt)

• Komplexitätsklasse NP-Vollständig (NP-C [complete]): Schwierigste Probleme in NP, wenn Q<math>\in</math>NP-C kann man mit Algorithmus für Q indirekt auch jedes andere Problem in NP lösen

R<math>\in</math>NP <math>\rightsquigarrow</math>Q(R)<math>\in</math>NP-C (Reduktion)

<math>\downarrow</math>

Lösung (R) <math>\rightsquigarrow</math> Lösung Q(R)

Reduktion muss effizient funktionieren, d.h. O(<math>\N^D</math>)

• Komplexitätsklasse NP-Schwer (NP-hard): mindestens so schwer wie NP-C, aber nicht unbedingt <math>\in</math>NP

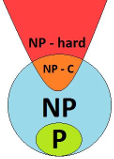Vereinfachung: NP enthält nur Entscheigungsprobleme: Fragen mit Ja/Nein-Antwort.

z.B.

TSP-Optimierungsproblem (NP-Schwer):

gegeben: gewichteter Graph

gesucht: kürzeste Rundreise

TSP-Entscheidungsproblem (NP-Vollständig):

gegeben: gewichteter Graph

<math>\exist</math>Rundreise <math>\le</math> 200kM, ist das wahr oder falsch?

Orakel: "Rundreise Z ist <math>\le</math>200kM" <math>\implies</math>leicht & effizient zu testen

Klassische Definition von NP: Probleme die von einer nicht-deterministischen Turingmaschine gelöst werden können (N = Nicht deterministisch, P = Polynomiell).

nicht deterministische Turingmaschine: formale Definition kompliziert <math>\rightarrow</math> Theoretische Informatik

anschaulich: TM kann in kritischen Situationen das Orakel fragen und sich vorsagen lassen

moderne Definition: "polynomiell Verifizierbar": es gibt effizienten Algorithmus, der für Probleme X und Entscheidungsfrage Y und Kandidatenlösung Z entscheidet, ob Z eine "ja-Antwort" bei Y impliziert.

Fall 1: korrekte Antwort auf Y ist "ja" (wissen wir aber nicht): <math>\exist</math>z: V(X, Y, Z) <math>\implies</math> OK

Z ist Beweis (proof/witness/certificate) dafür, dass Y die Antwort "ja" hat

liefert V(X, Y, Z) <math>\implies</math> falsch, ist Z kein Beweis und wir wissen noch nicht, ib Y mit "ja" oder "nein" zu beantworten ist.

Fall 2: korrekte Antwort auf Y ist "nein": <math>\forall</math>Z V(X, Y, Z) <math>\implies</math> falsch

<math>\implies</math> hat man einen Überprüfungsalgorithmus V, kann man X mit Y stets duch erschöpfende Suche ("brute-force") lösen

für jede mögliche Kandidatenlösung Z:

falls V(X, Y, Z) <math>\implies</math> ok:

return "ja"

return "nein"

<math>\uparrow</math> ineffizient, da es meist exponentiell viele Kandidaten Z gibt.

Erfüllbarkeitsproblem

(SAT-satisfyability) ist das kanonische NP-Vollständige Problem (Satz von Cook 1971)

• boolsche Variable x1 <math>\in</math>{true, false}, i=1,...,N (Problemgröße N-Bits)
• logische Ausdrücke Y über X mit Operatoren <math>\lnot</math>, <math>\and</math>, <math>\or</math>, <math>\implies</math>, <math>\leftrightarrow</math>, <math>\neq</math>, ()

z.B. N= 3, Y=(x1<math>\or</math>x2)<math>\and</math>(<math>\lnot</math>x1<math>\or</math>x2) <math>\implies</math> Z=(true[x1], true[x2], true[x3])

• Entscheidungsfrage: Gibt es eine Belegung con X sodass Y wahr ist?
• Bei komplizierten Problemen ist kein besserer Algorithmus bekannt als alle <math>2^N</math> Möglichkeiten zu probieren.
• Jede CPU kann als logische Schaltung geschrieben werden (damit auch jedes while-Programm)

Mit Gattern:

Jede logische Schaltung kann als SAT-Ausdruck geschrieben werden.

• Bsp.: Zuordnung von Heim und Auswärtsspielen beim Fußball

<math>x_{it} = \begin{cases}

true, & \mbox{Mannschaft i hat am Spieltag t Heimspiel} \\ false, & \mbox{Mannschaft i hat am Spieltag t Auswärtsspiel} \end{cases} </math>

1. Nebenbedingung: spielt Mannschaft i am Spieltag t gegen Mannschaft j, muss gelten <math> x_{it} = \lnot x_{jt}</math>

2. Nebenbedingung: Jede Mannschaft spielt gegen jede

3. Nebenbedingung: Jede Mannschaft spielt abwechselnd Heim und auswärts <math> x_{it} \neq x_{i(t+1)} </math>

Alle Bedingungen sollen gleichzeitig Erfüllt sein:

<math>y = \begin{cases} (x_{11} \neq x_{21}) \and (x_{31} \neq x_{41}) \and ... \\

( x_{12} \neq x_{32} ) \and ... \\ ( x_{11} \neq x_{12} ) \and ( x_{12} \neq x_{13} ) \and ... \end{cases}</math>

Frage: Kann man X so belegen, dass Y wahr ist?

<math>\rightarrow</math> Nein, nur möglich wenn es nur 2 Mannschaften gibt und diese abwechselnd gegeneinander antreten.

Normalformen für logische Ausdrücke zur Vereinfachung und Systematisierung

• 3-CNF (Konjunktionen-NF)
  • jede Klausel enthält max 3 Variablen (genau 3 mit dummy Variablen)
  • jede Klausel enthält nur <math> \or </math> und <math> /lnot </math>
  • alle Klauseln sind durch <math> \and </math> verknüpft.

z.B. <math> ( x_1 \or x_2 \or \lnot x_4 ) \and ( \lnot x_2 \or x_3 \or x_4) \and (...) \and </math>

<math> \Rightarrow </math> Ausdruck ist wahr, wenn jede Klausel wahr ist.

In jeder Klausel hat man 3 Chancen die Klausel wahr zu machen.

Aber: Klauseln können sich widersprechen und nicht erfüllbar sein!

Satz: Jeder logische Ausdruck effizient (in pol. Zeit) in 3-CNF umwandelbar.

Satz v. Cook: 3-SAT (Erfüllbarkeitsproblem für Ausdrücke in 3-CNF) ist NP-vollständig

zur Zeit ist kein effizienterer Algorithmus bekannt, als im schlechtesten Fall alle <math>2^N</math> Belegungen von {<math>x_i</math>} auszuprobieren

2-CNF: wie 3-CNF, nur 2 Variablen pro Klausel <math>\implies</math> effiziente Alg existieren, aber nicht jeder logische Ausdruck in 2-CNF transformierbar.

z.B. Heim-Auswärtsproblem

INF (Implikationen-NF):

• 2 Variablen pro Klausel, Operatoren <math> \implies und \lnot </math>
• Klauseln mit <math> \and </math> verknüpft.

Satz: jede 2-CNF effizient in INF umwandelbat.

<math> ( x_i \or x_j ) \rightsquigarrow ( \lnot x_i \implies x_j ) \and ( \lnot x_j \implies x_i )

</math> <math>\implies</math> INF als gerichteter Graph schreibbar und mittels starker Zusammenhangskomponenten lösbar.

3-SAT ist NP vollständig

Skizze des Beweises:

1. Unsere Algorithmen können auf einer Turingmaschine ausgeführt werden (äquivalent zur Turingmaschine: λ-Kalkül, while-Programm usw.)
2. Die Turingmaschine und ein gegebenes (festes) Programm können als logische Schaltung (Schaltnetz) implementiert werden, „Algorithmus in Hardware gegossen“
3. Jedes Schaltnetzwerk kann als logische Formel geschrieben werden, z.B.:

4. Jede logische Formel kann in 3-CNF umgewandelt werden

=> Jedes algorithmische Entscheidungsproblem kann als 3-SAT-Problem geschrieben werden.