NP-Vollständigkeit: Difference between revisions
(removed test edit) |
|||
| Line 1: | Line 1: | ||
== Das Problem des Handlungsreisenden == | |||
'''(engl.: Traveling Salesman Problem; abgekürzt: TSP)'''<br\> | |||
[http://de.wikipedia.org/wiki/Problem_des_Handlungsreisenden Wikipedia (de)] | |||
[http://en.wikipedia.org/wiki/Prim%27s_algorithm (en)] | |||
[[Image:TSP_Deutschland_3.PNG|thumb|200px|right|Optimaler Reiseweg eines Handlungsreisenden([http://de.wikipedia.org/w/index.php?title=Bild:TSP_Deutschland_3.PNG&filetimestamp=20070110124506 Quelle])]] | |||
*Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden. | |||
*Hierbei soll ein Handlungsreisender nacheinander ''n'' Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden. | |||
*Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen. | |||
:<u>''gegeben''</u>: zusammenhängender, gewichteter Graph (oft vollständiger Graph) | |||
:<u>''gesucht''</u>: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\> | |||
:auch genannt: kürzester Hamiltonkreis | |||
::- durch psychologische Experimente wurde herausgefunden, dass Menschen (in 2D) ungefähr proportionale Zeit zur Anzahl der Knoten brauchen, um einen guten Pfad zu finden, der typischerweise nur <math>\lesssim 5%</math> länger als der optimale Pfad ist<br\> | |||
:<u>''vorgegeben''</u>: Startknoten (kann willkürlich gewählt werden), vollständiger Graph | |||
::::: => v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger... | |||
:::::also <math>\frac{(v-1)!}{2}</math> mögliche Wege in einem vollständigen Graphen | |||
*Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird. | |||
*Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität. | |||
=== Approximationsalgorithmus === | |||
Für viele Probleme in der Praxis sind keine effizienten Algorithmen bekannt | |||
(NP-schwer). Diese (z.B. TSP) werden mit Approximationsalgorithmen berechnet, | |||
die effizient berechenbar sind, aber nicht unbedingt die optimale | |||
Lösung liefern. Beispielsweise ist es relativ einfach, eine Tour zu finden, die höchstens um den Faktor zwei länger ist als die optimale Tour. Die Methode beruht darauf, dass einfach der minimale Spannbaum ermittelt wird. | |||
'''Approximationsalgorithmus für TSP'''<br\> | |||
* TSP für ''n'' Knoten sei durch Abstandsmatrix D = <math>(d_{ij}) 1 \le i, j \le n</math> | |||
:gegeben (vollständiger Graph mit ''n'' Knoten, <math>d_{ij}</math> = Kosten der Kante (i,j)) <br\> | |||
:''gesucht:'' Rundreise mit minimalen Kosten. Dies ist NP-schwer!<br\> | |||
* D erfüllt die Dreiecksungleichung <math> \Leftrightarrow d_{ij} + d_{jk} \geq d_{ik} \text{ fuer } \forall{i, j, k} \in \lbrace 1, ..., n \rbrace</math> <br\> | |||
* Dies ist insbesondere dann erfüllt, wenn D die Abstände bezüglich einer Metrik darstellt oder D Abschluss einer beliebigen Abstandsmatrix C ist, d.h. :<math>d_{ij}</math> = Länge des kürzesten Weges (bzgl. C) von i nach j. | |||
*Die ”Qualität”der Lösung mit einem Approximationsalgorithmus ist höchstens um einen konstanten Faktor schlechter ist als die des Optimums. | |||
=== Systematisches Erzeugen aller Permutationen === | |||
*Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\> | |||
*'''Trick''': interpretiere jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\> | |||
*Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst. | |||
<u>''gegeben''</u>: zwei Wörter a, b der Länge n=len(a) bzw. m=len(b). Sei k = min(n,m) (im Spezialfall des Vergleichs von Permutationen gilt k = n = m)<br\> | |||
Mathematische Definition, wie die Wörter im Wörterbuch sortiert sind: <br\> | |||
:::<math>a<b \Leftrightarrow | |||
\begin{cases} | |||
n < m & \text{ falls fuer } 0 \le i \le k-1 \text{ gilt: } a[i] = b[i] \\ | |||
a[j] < b[j] & \text{ falls fuer } 0 \le i \le j-1 \text{ gilt: } a[i] = b[i], \text{ aber fuer ein } j<k: a[j] \ne b[j] | |||
\end{cases}</math><br\> | |||
Algorithmus zur Erzeuguung aller Permutationen: | |||
# beginne mit dem kleinsten Wort bezüglich der lexikographischen Ordnung => das ist das Wort, wo a aufsteigend sortiert ist | |||
# definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt | |||
Beispiel: Die folgenden Permutationen der Zahlen 1,2,3 sind lexikographisch geordnet | |||
1 2 3 6 Permutationen, da 3! = 6 | |||
1 3 2 | |||
2 1 3 | |||
2 3 1 | |||
3 1 2 | |||
3 2 1 | |||
----- | |||
0 1 2 Position | |||
Die lexikographische Ordnung wird deutlicher, wenn wir statt dessen die Buchstaben a,b,c verwenden: | |||
abc | |||
acb | |||
bac | |||
bca | |||
cab | |||
cba | |||
Eine Funktion, die aus einer gegebenen Permutation die in lexikographischer Ordnung nächst folgende erzeugt, kann wie folgt implementiert werden: | |||
def next_permutation(a): | |||
i = len(a) -1 #letztes Element; man arbeitet sich von hinten nach vorne durch | |||
while True: # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird | |||
if i <= 0: return False # a ist letzte Permutation | |||
i -= 1 | |||
if a[i]<a[i+1]: break | |||
#lexikogr. Nachfolger hat größeres a[i] | |||
j = len(a) | |||
while True: | |||
j -= 1 | |||
if a[i] < a[j]: break | |||
a[i], a[j] = a[j], a[i] #swap a[i], a[j] | |||
#sortiere aufsteigend zwischen a[i] und Ende | |||
#zur Zeit absteigend sortiert => invertieren | |||
i += 1 | |||
j = len(a) -1 | |||
while i < j: | |||
a[i], a[j] = a[j], a[i] | |||
i += 1 | |||
j-= 1 | |||
return True # eine weitere Permutation gefunden | |||
def naiveTSP(graph): | |||
start = 0 | |||
result = range(len(graph))+[start] | |||
rest = range(1,len(graph)) | |||
c = pathCost(result, graph) | |||
while next_permutation(rest): | |||
r = [start]+rest+[start] | |||
cc = pathCost(r, graph) | |||
if cc < c: | |||
c = cc | |||
result = r | |||
return c, result | |||
'''Komplexität''': <math>(v-1)!</math> Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also | |||
<math>O(v!) = O(v^v)</math> | |||
;Beispiel: | |||
{| | |||
|- | |||
| | i = 0 || | ||| ||| j = 3 || | |||
|- | |||
|| ↓ || || || ↓ || | |||
|- | |||
| style="background:silver; color:white" | 1 ||style="background:silver; color:white" | 4 ||style="background:silver; color:white"| 3 ||style="background:silver; color:white" | 2 || #input für next_permutation | |||
|- | |||
|- | |||
|| || i = 2 || || j = 3 || | |||
|- | |||
|| || ↓|| || ↓ || | |||
|- | |||
|- | |||
| style="background:silver; color:white" | 2 ||style="background:silver; color:white" | 4 ||style="background:silver; color:white"| 3 ||style="background:silver; color:white" | 1|| # vertauschen der beiden Elemente | |||
|- | |||
|- | |||
|| || ||i = 2 || || | |||
|- | |||
|| || ||j = 2 || || | |||
|- | |||
|| || || ↓|| || | |||
|- | |||
| style="background:silver; color:white" | 2 ||style="background:silver; color:white" | 1 ||style="background:silver; color:white"| 3 ||style="background:silver; color:white" | 4|| #absteigend sortiert | |||
|} | |||
=== Stirling'sche Formel === | |||
[http://de.wikipedia.org/wiki/Stirling-Formel Wikipedia (de)] | |||
[http://en.wikipedia.org/wiki/Stirling%27s_approximation (en)] | |||
Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Stirling'sche Formel z.T. starke Vereinfachungen erzielen. | |||
<math>v! \approx \sqrt{2 \pi v} \left(\frac{v}{e}\right)^v</math> | |||
: <math>O(v!) = O\left(\sqrt{v}\left(\frac{v}{e}\right)^v\right) \approx O(v^v)</math> | |||
== Die Problemklassen P und NP == | == Die Problemklassen P und NP == | ||
Revision as of 13:56, 22 July 2012
Das Problem des Handlungsreisenden
(engl.: Traveling Salesman Problem; abgekürzt: TSP)<br\> Wikipedia (de) (en)
- Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden.
- Hierbei soll ein Handlungsreisender nacheinander n Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden.
- Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen.
- gegeben: zusammenhängender, gewichteter Graph (oft vollständiger Graph)
- gesucht: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\>
- auch genannt: kürzester Hamiltonkreis
- - durch psychologische Experimente wurde herausgefunden, dass Menschen (in 2D) ungefähr proportionale Zeit zur Anzahl der Knoten brauchen, um einen guten Pfad zu finden, der typischerweise nur <math>\lesssim 5%</math> länger als der optimale Pfad ist<br\>
- vorgegeben: Startknoten (kann willkürlich gewählt werden), vollständiger Graph
- => v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger...
- also <math>\frac{(v-1)!}{2}</math> mögliche Wege in einem vollständigen Graphen
- Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird.
- Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität.
Approximationsalgorithmus
Für viele Probleme in der Praxis sind keine effizienten Algorithmen bekannt (NP-schwer). Diese (z.B. TSP) werden mit Approximationsalgorithmen berechnet, die effizient berechenbar sind, aber nicht unbedingt die optimale Lösung liefern. Beispielsweise ist es relativ einfach, eine Tour zu finden, die höchstens um den Faktor zwei länger ist als die optimale Tour. Die Methode beruht darauf, dass einfach der minimale Spannbaum ermittelt wird.
Approximationsalgorithmus für TSP<br\>
- TSP für n Knoten sei durch Abstandsmatrix D = <math>(d_{ij}) 1 \le i, j \le n</math>
- gegeben (vollständiger Graph mit n Knoten, <math>d_{ij}</math> = Kosten der Kante (i,j)) <br\>
- gesucht: Rundreise mit minimalen Kosten. Dies ist NP-schwer!<br\>
- D erfüllt die Dreiecksungleichung <math> \Leftrightarrow d_{ij} + d_{jk} \geq d_{ik} \text{ fuer } \forall{i, j, k} \in \lbrace 1, ..., n \rbrace</math> <br\>
- Dies ist insbesondere dann erfüllt, wenn D die Abstände bezüglich einer Metrik darstellt oder D Abschluss einer beliebigen Abstandsmatrix C ist, d.h. :<math>d_{ij}</math> = Länge des kürzesten Weges (bzgl. C) von i nach j.
- Die ”Qualität”der Lösung mit einem Approximationsalgorithmus ist höchstens um einen konstanten Faktor schlechter ist als die des Optimums.
Systematisches Erzeugen aller Permutationen
- Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\>
- Trick: interpretiere jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\>
- Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst.
gegeben: zwei Wörter a, b der Länge n=len(a) bzw. m=len(b). Sei k = min(n,m) (im Spezialfall des Vergleichs von Permutationen gilt k = n = m)<br\> Mathematische Definition, wie die Wörter im Wörterbuch sortiert sind: <br\>
- <math>a<b \Leftrightarrow
\begin{cases} n < m & \text{ falls fuer } 0 \le i \le k-1 \text{ gilt: } a[i] = b[i] \\ a[j] < b[j] & \text{ falls fuer } 0 \le i \le j-1 \text{ gilt: } a[i] = b[i], \text{ aber fuer ein } j<k: a[j] \ne b[j] \end{cases}</math><br\>
Algorithmus zur Erzeuguung aller Permutationen:
- beginne mit dem kleinsten Wort bezüglich der lexikographischen Ordnung => das ist das Wort, wo a aufsteigend sortiert ist
- definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt
Beispiel: Die folgenden Permutationen der Zahlen 1,2,3 sind lexikographisch geordnet
1 2 3 6 Permutationen, da 3! = 6 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 ----- 0 1 2 Position
Die lexikographische Ordnung wird deutlicher, wenn wir statt dessen die Buchstaben a,b,c verwenden:
abc acb bac bca cab cba
Eine Funktion, die aus einer gegebenen Permutation die in lexikographischer Ordnung nächst folgende erzeugt, kann wie folgt implementiert werden:
def next_permutation(a): i = len(a) -1 #letztes Element; man arbeitet sich von hinten nach vorne durch while True: # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird if i <= 0: return False # a ist letzte Permutation i -= 1 if a[i]<a[i+1]: break #lexikogr. Nachfolger hat größeres a[i] j = len(a) while True: j -= 1 if a[i] < a[j]: break a[i], a[j] = a[j], a[i] #swap a[i], a[j] #sortiere aufsteigend zwischen a[i] und Ende #zur Zeit absteigend sortiert => invertieren i += 1 j = len(a) -1 while i < j: a[i], a[j] = a[j], a[i] i += 1 j-= 1 return True # eine weitere Permutation gefunden def naiveTSP(graph): start = 0 result = range(len(graph))+[start] rest = range(1,len(graph)) c = pathCost(result, graph) while next_permutation(rest): r = [start]+rest+[start] cc = pathCost(r, graph) if cc < c: c = cc result = r return c, result
Komplexität: <math>(v-1)!</math> Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also
<math>O(v!) = O(v^v)</math>
- Beispiel
| i = 0 | j = 3 | |||
| ↓ | ↓ | |||
| 1 | 4 | 3 | 2 | #input für next_permutation |
| i = 2 | j = 3 | |||
| ↓ | ↓ | |||
| 2 | 4 | 3 | 1 | # vertauschen der beiden Elemente |
| i = 2 | ||||
| j = 2 | ||||
| ↓ |
| |||
| 2 | 1 | 3 | 4 | #absteigend sortiert |
Stirling'sche Formel
Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Stirling'sche Formel z.T. starke Vereinfachungen erzielen. <math>v! \approx \sqrt{2 \pi v} \left(\frac{v}{e}\right)^v</math>
- <math>O(v!) = O\left(\sqrt{v}\left(\frac{v}{e}\right)^v\right) \approx O(v^v)</math>
Die Problemklassen P und NP
- fundamentale Unterscheidung:
- Komplexität O(<math>n^p</math>), p < ∞ (n = Problemgröße), ⇒ ist eventuell effizient
- exponentielle Komplexität O(<math>2^n</math>), O(<math>2^{\sqrt{n}}</math>), ⇒ prinzipiell nicht effizient
- Vereinfachung:
- betrachte nur Entscheidungsprobleme, d.h. Algorithmen, die True/False liefern
- z.B. BP: „Gibt es einen Pfad der Länge ≤ L?“
- Klasse P: alle Algorithmen, die in polynomieller Zeit eine Lösung finden,
- Klasse NP: Alle Algorithmen, wo man eine gegebene Lösung in polynomieller Zeit überprüfen kann
- Ungelöstes Problem: Sind alle Probleme in NP auch in P? („P = NP?“)
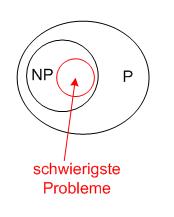
- Welches sind die schwierigsten Probleme in NP?
- => die, sodass man alle anderen NP-Probleme in diese umwandeln kann: „NP vollständig“, „NP complete“
- umwandeln:
- Problem wird auf ein anderes reduziert
- Reduktion darf nur polynomielle Zeit erfordern (d.h. alle Zwischenschritte müssen polynomiell sein)
3-SAT ist NP vollständig
Skizze des Beweises:
- Unsere Algorithmen können auf einer Turingmaschine ausgeführt werden (äquivalent zur Turingmaschine: λ-Kalkül, while-Programm usw.)
- Die Turingmaschine und ein gegebenes (festes) Programm können als logische Schaltung (Schaltnetz) implementiert werden, „Algorithmus in Hardware gegossen“
- Jedes Schaltnetzwerk kann als logische Formel geschrieben werden, z.B.:
- 4. Jede logische Formel kann in 3-CNF umgewandelt werden
- => Jedes algorithmische Entscheidungsproblem kann als 3-SAT-Problem geschrieben werden.