Randomisierte Algorithmen: Difference between revisions

Revision as of 09:22, 14 August 2010

1. Randomisierte Algorithmen

Def.: Algorithmen, die bei Entscheidung oder bei der Wahl der Parameter Zufallszahlen benutzen

Bsp.: Lösen des K-SAT-Problems durch RA

   geg.: logischer Ausdruck in K-CNF (n Variablen, m Klauseln, k Variablen pro Klausel)

    $\underbrace {\underbrace {\left(x_{1}\vee x_{3}\vee ...\right)} _{k\;Variablen}\wedge \left(x_{2}\vee x_{4}\vee ...\right)} _{m\;Klauseln}$

   for i in range (trials):    #Anzahl der Versuche
        #Bestimme eine Zufallsbelegung des  $\{x_{i}\}$ :
        for j in range (steps):
              if  $\{x_{i}\}$  erfüllt alle Klauseln: return  $\{x_{i}\}$ 
              #wähle zufällig eine Klausel, die nicht erfüllt ist und negiere zufällig eine der Variablen in dieser Klausel 
              (die Klausel ist jetzt erfüllt)
   return None

Eigenschaft: falls $k>2$ : steps *trials $\in O\left(\mathrm {A} ^{n}\right)\mathrm {A} >1$

z.B. $k=3$ steps=3*n, trials= $\left({\frac {4}{3}}\right)^{n}$

aber: bei $k=2$ sind im Mittel nur steps= $O\left(n^{2}\right)$ nötig, trials= $O\left(1\right)$

-Zufallsbelegung hat $t\leq n$ richtige Variablen (im Mittel $t\approx {\frac {n}{2}}$ )

Negieren einer Variable ändert t um 1, u.Z. $t\rightarrow t+1$ mit Wahrscheinlichkeit ${\frac {1}{2}}$ ::(für beliebiges k: ${\frac {1}{k}}$ )

t\rightarrow t-1

mit Wahrscheinlichkeit

{\frac {1}{2}}

::(für beliebiges k:

{\frac {k-1}{k}}

)

-Wieviele Schritte braucht man im Mittel, um zu einer Lösung mit t Richtigen zu kommen?

       $S\left(t\right)={\frac {1}{2}}S\left(t-1\right)+{\frac {1}{2}}S\left(t+1\right)+1$ 
      
       $S\left(n\right)=0$     #Abbruchbedingung der Schleife
      
       $S\left(0\right)=S\left(1\right)+1\Rightarrow S\left(t\right)=n^{2}-t^{2}$

      Probe: 

       ${\begin{aligned}S\left(n\right)&=n^{2}-n^{2}=0\\S\left(0\right)&=n^{2}-0^{2}\\&=S\left(1\right)+1\\&=n^{2}-1^{2}+1\\&=n^{2}\\S\left(t\right)&={\frac {1}{2}}\left(n^{2}-\left(t-1\right)^{2}\right)+{\frac {1}{2}}\left(n^{2}-\left(t+1\right)^{2}\right)+1\\&={\frac {1}{2}}n^{2}-{\frac {1}{2}}\left(t^{2}-2t+1\right)+{\frac {1}{2}}n^{2}-{\frac {1}{2}}\left(t^{2}+2t+1\right)+1\\&=n^{2}-t^{2}\end{aligned}}$

Das ist das Random Walk Problem

Im ungünstigsten Fall (t=0) werden im Mittel $n^{2}$ Schritte benötigt, um durch random walk nach t=n zu gelangen.

2. RANSAC-ALGORITHMUS (Random Sample Consensus)

Aufgabe: gegeben: Datenpunkte

gesucht: Modell, das die Datenpunkte erklärt

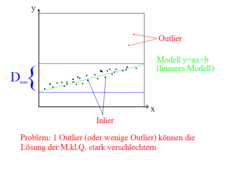
Messpunkte:

     übliche Lösung: Methode der kleinsten Quadrate
     
      $\min _{a,b}\sum _{i}\left(ax_{i}+b+y_{i}\right)^{2}$ 
     
     Schulmathematik:       $Minimum{\stackrel {\wedge }{=}}Ableitung=0$

Lineares Gleichungssystem

${\frac {d}{da}}\sum {i}\left(ax_{i}+b-y_{i}\right)^{2}=\sum {i}{\frac {d}{da}}\left[ax_{i}+b-y_{i}\right)^{2}$

f\left(g\left(x\right)\right)

f\left(x\right)=x^{2}

y\left(a\right)=ax_{i}+b-y_{i}

$=\sum _{i}2\left(ax_{i}+b-y_{i}\right){\frac {d}{da}}\underbrace {ax_{i}+b-y_{i}} _{x_{i}}$

${\underline {=2\sum _{i}\left(ax_{i}+b-y_{i}\right)x_{i}{\stackrel {!}{=}}0}}$

a\sum _{i}{x_{i}}^{2}+b\sum _{i}x_{i}=\sum _{i}x_{i}y_{i}

a\sum _{i}x_{i}+b\sum _{i}1=\sum _{i}y_{i}

${\frac {d}{db}}\sum _{i}\left(ax_{i}+b-y_{i}\right)^{2}=2\sum _{i}\left(ax_{i}+b-y_{i}\right)*1$

Problem:

\epsilon \%

der Datenpunkte sind Outlier

\Longrightarrow

Einfaches Anpassen des Modells an die Datenpunkte funktioniert nicht

Seien mindestens k Datenpunkte notwendig, um das Programm anpassen zu können

RANSAC-Algorithmus

     for  l in range (trials):
          wähle zufällig k Punkte aus
          passe das Modell an die k Punkte an
          zähle, wieviele Punkte in der Nähe des Modells liegen (d.h.  $d_{i}<d_{m}ax$  muss geschickt gewählt werden) 
                                          #Bsp. Geradenfinden:-wähle a,b aus zwei Punkten
                                                              -berechne:  $|ax_{i}+b-y_{i}|=d_{i}$ 
                                                              -zähle Punkt i als Inlier, falls  $d_{i}<d_{m}a$ 
     return: Modell mit höchster Zahl der Inlier

      $trials={\frac {log\left(1-p\right)}{log\left(1-\left(1-\epsilon \right)^{k}\right)}}$   mit k=Anzahl der Datenpunkte und p=Erfolgswahrscheinlichkeit,  $\epsilon$ =Outlier-Anteil

Erfolgswahrscheinlichkeit: p=99%

${\begin{array}{|c||c|c|c|c|c|}Beispiel&k&\epsilon =10\%&20\%&50\%&70\%\\\hline Linie\;in\;2D&2&3&5&17&49\\Kreis\;in\;2D&3&4&7&35&169\\Ebene\;in\;3D&8&9&26&1172&70188\\\end{array}}$

Ein Spiel: Wie viel Schritte braucht man im Mittel zum Ziel?

  geg.: 5 Plätze, 2 Personen: eine Person rückt vom einem Platz zu dem enderen Platz;
        die zweite Person wirft die Münze.
        Wenn die Münze auf Kopf landet, rücke nach rechts und wenn die Münze auf Zahl landet, rücke nach links.
        <--- Zahl                                                         Kopf-->
        Kopf: /////
        Zahl: ///

=> mit 8 Schritten bis zum Ziel

im Mittel: bei N Plätzen braucht man N² Schritte

all: mit N² Schritten um N Plätze rücken

Wie viel Schritte braucht man im Mittel zum Ziel?

         $S\left(N\right)=0$     #wenn wir uns im Stuhl Nr.1 befinden
          
         $S\left(i\right)={\frac {1}{2}}S\left(1+S\left(i+1\right)\right)+{\frac {1}{2}}S\left(1+S\left(i-1\right)\right)={\frac {1}{2}}S\left(i+1\right)+{\frac {1}{2}}S\left(i-1\right)+1$

         $S\left(0\right)=1+S\left(1\right)$     #bei 0.Platz

Lösung:

         $S\left(i\right)=N^{2}-i^{2}$

speziell:

         $S\left(i\right)=N^{2}$            #wenn man am ungünstigsten Platz startet

Beziehung zu randomisiertem 2-SAT

     "Platz  $i$  ":  $i$  Variablen haben den richtigen Wert,   $\left(N-i\right)$   sind falsch gesetzt

      $S\left({\frac {N}{2}}\right)=N^{2}-\left({\frac {N}{2}}\right)^{2}=N^{2}-{\frac {N}{4}}^{2}={\frac {3}{4}}N^{2}$ 
      $S\left({\frac {N}{2}}\right)$      # Anfangszustand

Las Vegas vs. Monte Carlo

  * Las Vegas - Algorithmen
    - Ergebnis ist immer korrekt.
    - Berechnung ist mit hoher Wahrscheinlichkeit effizient (d.h. Randomisierung macht den ungünstigsten Fall unwahrscheinlich).

  * Monte Carlo - Algorithmen
    - Berechnung immer effizient.
    - Ergebnis mit hoher Wahrscheinlichkeit korrekt (falls kein effizienter Algorithmus bekannt, der immer die richtige Lösung liefert).

Las Vegas	Monte Carlo
- Erzeugen einer perfekten Hashfuktion	- Algorithmus von Freiwald(Matrizenmultiplikation)
- universelles Hashing	- RANSAC
- Quick Sort mit zufälliger Wahl des Pivot-Elements	- randomisierte K-SAT(k>=3)(Alg. von Schöning)
- Treep mit zufälligen Prioritäten	-

Zufallszahlen

- kann man nicht mit deterministischen Computern erzeugen

- aber man kann Pseudo-Zufallszahlen erzeugen, die viele Eigenschaften von echten Zufallszahlen haben

* sehr ähnlich zum Hash

    "linear Conguential Random number generator"
        $I_{i+1}=\left(a*I_{i}+c\right)modm$ 
        ${\begin{array}{ll}\mathrm {=>} &I_{i}\in [0,m-1]\\\end{array}}$

-sorgfältige Wahl von a, c, m notwendig

Bsp. m = 2³²

a = 1664525, c = 1013904223

"quick and dirty generator"

Nachteile

nicht zufällig genug für viele Anwendungen

Bsp. wähle Punkt in R³

{\begin{array}{ll}\mathrm {} &p=(rand(),rand(),rand())\\\end{array}}

gibt Zahl u, v, w so, dass

{\begin{array}{ll}\mathrm {} &u*p[0]+v*p[1]+w*p[3]\\\end{array}}

stark geclustert ist.

Periodenlänge ist zu kurz:

spätestens nach m Schritten wiederholt sich die Folge

allgemein: falls der interne Zustand des Zufallsgenerators k bits hat, ist Periodenlänge:

{\begin{array}{ll}\mathrm {} &Periode<2^{k}\\\end{array}}

lowbits sind weniger zufällig als die highbits

Mersenne Twister

bester zur Zeit bekannter Zufallszahlengenerator (ZZG)

innere Zustand: ${\begin{array}{ll}\mathrm {} &624*32bit\ Integers=>19968bits\\\end{array}}$

Periodenlänge: $2^{19937}\approx 4*10^{6000}$

Punkte aus aufeinanderfolgende Zufallszahlen in $\mathbb {R} ^{n}$ sind gleich verteilt bis ${\begin{array}{ll}\mathrm {} &n=623\\\end{array}}$

alle Bits sind unabhängig voneinander zufällig ("Twister")

schnell

 class Random:
   def __init__(self, seed):
       self.N = 624
       self.state = [0]*624
       self.state = zufällig mit Hilfe des seeds initialisieren (einfacher ZZG)
       self.i = 0    # zählt mit in welchem Zustand wir gerade aufhalten

   def __call__(self):
       N,M = 624, 397
       i = self.i
       r = (self.state[i] & 0x80000000)|(self.state[(i+1)%N] & 0x7FFFFFFF)     # aktualisieren
       if self.state[(i+1)%N]&1:                                               # des Zustands
          r^= 0x9908B0DF
       self.state[i] = self.state[(i+1)%N]*^r

       y = self.state[i]
          self.i = (self.i + 1)%N
          # bits verwürfeln
          y ^= (y>>11)
          y ^= ((y>>7) & 0x9D2C5680)
          y ^= ((y>>15) & 0xEFC60000)
          y ^= (y>>18)
        return y

geg.: Zufallszahl ${\begin{array}{ll}\mathrm {} &[0,\overbrace {2^{32}-1} ^{m-1}]\\\end{array}}$

ges.: Zufallszahl ${\begin{array}{ll}\mathrm {} &[0,k-1]\\\end{array}}$

naive Lösung: ${\begin{array}{ll}\mathrm {} &rand()\%k\\\end{array}}$ ist schlecht.

Bsp. ${\begin{array}{ll}\mathrm {} &\qquad m=16\qquad k=11\\\end{array}}$

rand()	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
rand()%k	0	1	2	3	4	5	6	7	8	9	10	0	1	2	3	4

=> 0,...,n kommt doppelt so häufig wie 5,...,10 "nicht zufällig"

Lösung: Zurückweisen des Rests der Zahlen (rejektion sampling)

${\begin{array}{ll}\mathrm {} &remainder=(m-1-(k-1))\%k=(m-k)\%k\\\mathrm {} &last\ Good\ Value=m-1-remainder\\\end{array}}$

 r = rand()
 while r > last.GoodValue:
       r = rand()
       return r%k

Nächstes Thema

@@ Line 40: / Line 40: @@
         <math>S\left(n\right)=0</math>    #Abbruchbedingung der Schleife
-        <math>S\left(0\right) = S\left( 1\right) + 1 \Longrightarrow S\left(t\right) = n^2-t^2</math>
+        <math>S\left(0\right) = S\left( 1\right) + 1 \Rightarrow S\left(t\right) = n^2-t^2</math>
-        '''Probe:''' <math>S\left(n\right)=n^2-n^2=0</math>
+        '''Probe:'''
+       <math>
+       \begin{align}
+             S\left(n\right) & = n^2-n^2=0 \\
-              <math>S\left(0\right) =n^2-0^2</math>
+             S\left(0\right) &= n^2-0^2 \\
-                    <math>=S\left(1\right)+1</math>
+                    &= S\left(1\right)+1 \\
-                    <math>\;=n^2-1^2+1</math>
+                    &= n^2-1^2+1 \\
-                    <math>\;=n^2</math>
+                    &= n^2 \\
-               <math>S\left(t\right)=\frac 1 2 \left(n^2-\left(t-1\right)^2\right) + \frac 1 2 \left(n^2-\left(t+1\right)^2\right)+1</math>
+               S\left(t\right) &= \frac 1 2 \left(n^2-\left(t-1\right)^2\right) + \frac 1 2 \left(n^2-\left(t+1\right)^2\right)+1 \\
-                    <math>=\frac 1 2 n^2-\frac 1 2 \left( t^2-2t+1\right) + \frac 1 2 n^2-\frac 1 2</math>
+                    &= \frac 1 2 n^2-\frac 1 2 \left( t^2-2t+1\right) + \frac 1 2 n^2-\frac 1 2 \left(t^2+2t+1\right) + 1 \\
-                    <math>=\left(t^2+2t+1\right)</math>
+                    &= n^2-t^2
+       \end{align}</math>
-                   <math>\;=n^2-t^2</math>

Randomisierte Algorithmen: Difference between revisions

Revision as of 09:22, 14 August 2010

Contents

1. Randomisierte Algorithmen

2. RANSAC-ALGORITHMUS (Random Sample Consensus)

Las Vegas vs. Monte Carlo

Zufallszahlen

Nachteile

Mersenne Twister

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

Tools