Graphen und Graphenalgorithmen

Einführung zu Graphen

Motivation -- Königsberger Brückenproblem

Leonhard Euler [1] erfand den Graphen-Formalismus 1736, um eine scheinbar banale Frage zu beantworten: Ist es möglich, in Königsberg (siehe Abbildung) einen Spaziergang zu unternehmen, bei dem jede der 7 Brücken genau einmal überquert wird?

Ein Graph abstrahiert von der Geometrie des Problems und repräsentiert nur die Topologie. Jeder Stadtteil von Königsberg ist ein Knoten des Graphen, jede Brücke eine Kante. Der zum Brückenproblem gehörende Graph sieht also so aus:

    O
   /| \
   \|  \
    O---O
   /|  /
   \| /
    O

Der gesuchte Spaziergang würde existieren, wenn es maximal 2 Knoten gäbe, an denen sich eine ungerade Zahl von Kanten trifft. Die Frage muss für Königsberg also verneint werden, denn hier gibt es vier solche Knoten.

Inzwischen haben Graphen ein riesige Zahl weiterer Anwendungen gefunden. Einige Beispiele:

• Landkarten:
  • Knoten: Länder
  • Kanten: gemeinsame Grenzen

• Logische Schaltkreise:
  • Knoten: Gatter
  • Kanten: Verbindungen

• Chemie (Summenformeln):
  • Knoten: chemische Elemente
  • Kanten: Bindungen

• Soziologie (StudiVZ)
  • Soziogramm
    • Knoten: Personen
    • Kanten: Freund von ...

Definitionen

Ungerichteter Graph

Ein ungerichteter Graph G = ( V, E ) besteht aus

• einer endliche Menge V von Knoten (vertices)
• einer endlichen Menge <math>E \subset V \times V</math> von Kanten (edges)

Die Paare (u,v) und (v,u) gelten dabei als nur eine Kante (somit gilt die Symmetriebeziehung: (u,v) ∈ E => (v,u) ∈ E ). Die Anzahl der Kanten, die sich an einem Knoten treffen, wird als Grad (engl. degree) dieses Knotens bezeichnet:

degree(v) = |{v' ∈ V | (v,v') ∈ E}|

(Die Syntax |{...}| bezeichnet dabei die Mächtigkeit der angegebenen Menge, also die Anzahl der Elemente in der Menge.)

Der Graph des Königsberger Brückenproblems ist ungerichtet. Bezeichnet man die Knoten entsprechend des folgenden Bildes

   c
  /| \
  \|  \
   b---d 
  /|  /
  \| /
   a

gilt für die Knotengrade: degree(a) == degree(c) == degree(d) == 3 und degree(b) == 5. Genauer muss man bei diesem Graphen von einem Multigraphen sprechen, weil es zwischen einigen Knotenpaaren (nämlich (a, b) sowie (b, c)) mehrere Kanten ("Mehrfachkanten") gibt. Wir werden in dieser Vorlesung nicht näher auf Multigraphen eingehen.

Gerichteter Graph

Ein Graph heißt gerichtet, wenn die Kanten (u,v) und (v,u) unterschieden werden. Die Kante (u,v) ∈ E wird nun als Kante von u nach v (aber nicht umgekehrt) interpretiert. Entsprechend unterscheidet man jetzt den eingehenden und den ausgehenden Grad jedes Knotens:

• out_degree(v) = |{v' ∈ V | (v,v') ∈ E}|
  
• in_degree(v) = |{v' ∈ V| (v',v) ∈ E}|

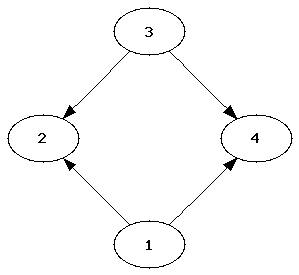
Das folgende Bild zeigt einen gerichteten Graphen. Hier gilt out_degree(1) == out_degree(3) == in_degree(2) == in_degree(4) == 2 und in_degree(1) == in_degree(3) == out_degree(2) == out_degree(4) == 0:

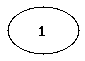
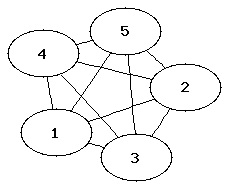
Vollständiger Graph

Ein vollständiger Graph ist ein ungerichteter Graph, bei dem jeder Knoten mit allen anderen Knoten verbunden ist.

<math>E = \{ (v,w) | v \in V, w \in V, v \ne w \}</math>

Ein vollständiger Graph mit |V| Knoten hat <math>|E| = \frac{|V|(|V|-1)}{2}</math> Kanten.

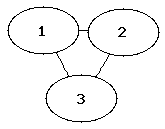
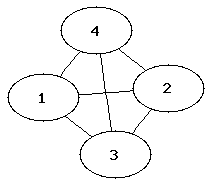
Die folgenden Abbildungen zeigen die vollständigen Graphen mit einem bis fünf Knoten (auch als K₁ bis K₅ bezeichnet).

k1	k2	k3
k4	k5

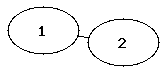Rätsel
Auf einer Party sind Leute. Alle stoßen miteinander an. Es hat 78 mal "Pling" gemacht. Wieviele Leute waren da? Antwort: Jede Person ist ein Knoten des Graphen, jedes Antoßen eine Kante. Da alle miteinander angestoßen haben, handelt es sich um einen vollständigen Graphen. Mit |V|(|V|-1)/2 = 78 folgt, dass es 13 Personen waren.

Gewichteter Graph

Ein Graph heißt gewichtet, wenn jeder Kante eine reelle Zahl zugeordnet ist. Bei vielen Anwendungen beschränkt man sich auch auf nichtnegative reelle Gewichte. In einem gerichteten Graphen können die Gewichte der Kanten (u,v) und (v,u) unterschiedlich sein.

Die Gewichte kodieren Eigenschaften der Kanten, die für die jeweilige Anwendung interessant sind. Bei der Berechnung des maximalen Flusses in einem Netzwerk sind die Gewichte z.B. die Durchflusskapazitäten jeder Kante, bei der Suche nach kürzesten Weges kodieren Sie den Abstand zwischen den Endknoten der Kante, bei Währungsnetzwerken (jeder Knoten ist eine Währung) geben sie die Wechselkurse an, usw..

Teilgraphen

Ein Graph G' = (V',E') ist ein Teilgraph eines Graphen G, wenn gilt:

• V' ⊆ V
• E' ⊂ E

Er heißt (auf)spannender Teilgraph, wenn gilt:

• V' = V

Er heißt induzierter Teilgraph, wenn gilt:

• e = (u,v) ∈ E' ⊂ E ⇔ u ∈ V' und v ∈ V'

Den von V' induzierten Teilgraphen erhält man also, indem man aus G alle Knoten löscht, die nicht in V' sind, sowie alle Kanten (und nur diese Kanten), die einen der gelöschten Knoten als Endknoten haben.

Wege, Pfade, Zyklen, Kreise, Erreichbarkeit

Sei G = (V,E) ein Graph (ungerichtet oder gerichteter) Graph. Dann gilt folgende rekursive Definition:

• Für v ∈ V ist (v) ein Weg der Länge 0 in G
• Falls <math>(v_0, v_1, ..., v_{n-1})</math> ein Weg ist, und eine Kante <math>(v_{n-1}, v_n)\in E</math> existiert, dann ist auch <math>(v_0, v_1, ..., v_{n-1}, v_n)</math> ein Weg, und er hat die Länge n.

Ein Weg ist also eine nichtleere Folge von Knoten, so dass aufeinander folgende Knoten stets durch eine Kante verbunden sind. Die Länge des Weges entspricht der Anzahl der Kanten im Weg (= Anzahl der Knoten - 1).

• Ein Pfad <math>(v_0, v_1, ..., v_{n-1}, v_n)</math> ist ein Weg, bei dem alle Knoten v_i verschieden sind.
• Ein Zyklus <math>(v_0, v_1, ..., v_{n-1}, v_n)</math> ist ein Weg, der zum Ausgangspunkt zurückkehrt, wenn also v₀ = v_n gilt.
• Ein Kreis ist ein Zyklus ohne Überkreuzungen. Das heisst, es gilt v₀ = v_n und <math>(v_0, v_1, ..., v_{n-1})</math> ist ein Pfad.
• Ein Knoten w ∈ V ist von einem anderen Knoten v ∈ V aus erreichbar genau dann, wenn ein Weg (v, ..., w) existiert. Wir schreiben dann <math>v \rightsquigarrow w</math>.

In einem ungerichteten Graph ist die Erreichbarkeits-Relation stets symmetrisch, das heisst aus <math>v \rightsquigarrow w</math> folgt <math>w \rightsquigarrow v</math>. In einem gerichteten Graphen ist dies im allgemeinen nicht der Fall.

Bestimmte Wege haben spezielle Namen

Eulerweg

Ein Eulerweg ist ein Weg, der alle Kanten genau einmal enthält.

Die eingangs erwähnte Frage des Königsberger Brückenproblems ist equivalent zu der Frage, ob der dazugehörige Graph einen Eulerweg besitzt (daher der Name). Ein anderes bekanntes Beispiel ist das "Haus vom Nikolaus": Wenn man diesen Graphen in üblicher Weise in einem Zug zeichnet, erhält man gerade den Eulerweg.

   O
  /  \
 O----O
 | \/ |
 | /\ |   "Das Haus vom Nikolaus": Alle Kanten werden nur einmal passiert
 O----O

Hamiltonweg

Ein Hamiltonweg ist ein Weg, der alle Knoten genau einmal enthält. Das "Haus vom Nikolaus" besitzt auch einen Hamiltonweg:

   O
  /   
 O----O
    /  
   /      Alle Knoten werden nur einmal passiert
 O----O

Hamiltonkreis

Ein Hamiltonkreis ist ein Kreis, der alle Knoten genau einmal enthält. Auch ein solches Gebilde ist im Haus von Nilolaus enthalten:

   O
  /  \
 O    O
 |    |   v0 = vn
 |    |   vi != vj   Für Alle i,j   i !=j; i,j >0; i,j < n
 O----O     

Die folgende Skizze zeigt hingegen einen Zyklus: Der Knoten rechts unten sowie die untere Kante sind zweimal enthalten (die Kante einmal von links nach rechts und einmal von rechts nach links):

   O
  /  \
 O    O
   \  |
    \ |   Zyklus
 O====O

Zusammenhang, Zusammenhangskomponenten

Ein ungerichteter Graph G heißt zusammenhängend, wenn für alle v,w ∈ V gilt:

<math>v \rightsquigarrow w</math>

Ein gerichteter Graph G ist zusammenhängend, wenn für alle v,w ∈ V gilt:

<math>v \rightsquigarrow w</math> oder <math>w \rightsquigarrow v</math>.

Er ist stark zusammenhängend, wenn für alle v,w ∈ V gilt:

<math>v \rightsquigarrow w</math> und <math>w \rightsquigarrow v</math>.

Entsprechende Definitionen gelten für Teilgraphen G'. Ein Teilgraph G' heisst Zusammenhangskomponente von G, wenn er ein maximaler zusammenhängender Teilgraph ist, d.h. wenn G' zusammenhängend ist, und man keine Knoten und Kanten aus G mehr zu G' hinzufügen kann, so dass G' immer noch zusammenhängend bleibt. Entsprechend definiert man starke Zusammenhangskomponenten in einem gerichteten Graphen.

Planarer Graph, ebener Graph

Ein Graph heißt planar, wenn er so in einer Ebene gezeichnet werden kann, dass sich die Kanten nicht schneiden (außer an den Knoten). Ein Graph heißt eben, wenn er tatsächlich so gezeichnet ist, dass sich die Kanten nicht schneiden. Die Einbettung in die Ebene ist im allgemeinen nicht eindeutig.

Beispiele:

Der folgende Graph ist planar und eben:

     O
    /|\
   / O \
  / / \ \
  O     O

Das "Haus vom Nikolaus" ist ebenfalls planar, wird aber üblicherweise nicht als ebener Graph gezeichnet, weil sich die Diagonalen auf der Wand überkreuzen:

   O
  /  \
 O----O
 | \/ |
 | /\ |   
 O----O

Eine ebene Einbettung dieses Graphen wird erreicht, wenn man eine der Diagonalen ausserhalb des Hauses zeichnet. Der Graph (also die Menge der Knoten und Kanten) ändert sich dadurch nicht.

     O  
    /  \
 --O----O
/  |  / |
|  | /  |   
|  O----O      Das "Haus vom Nikolaus" als ebener Graph gezeichnet.
 \     /
  -----

Eine alternative Einbettung erhalten wir, wenn wir die andere Diagonale außerhalb des Hauses zeichnen:

     O  
    /  \
   O----O--|
   | \  |  |
   |  \ |  | 
   O----O  |     Alternative Einbettung des "Haus vom Nikolaus".
   |       |
   |-------|

Jede Einbettung eines planaren Graphen (also jeder ebene Graph) definiert eine eindeutige Menge von Regionen:

|----O   @
|   /@ \
|  O----O
|  |@ / |
|  | / @|   
|  O----O        @ entspricht jeweils einer Region. Auch ausserhalb der Figur ist eine Region (die sogenannte unendliche Region).
|@      |
|-------|

Der vollständige Graph K5 ist kein planarer Graph, da sich zwangsweise Kanten schneiden, wenn man diesen Graphen in der Ebene zeichnet.

Dualer Graph

Jeder ebene Graph G = (V, E) hat einen dualen Graphen D = (V_D, E_D), dessen Knoten und Kanten wie folgt definiert sind:

• V_D enthält einen Knoten für jede Region des Graphen G
• Für jede Kante e ∈ E gibt es eine duale Kante e_D ∈ E_D, die die an e angrenzenden Regionen (genauer: die entsprechenden Knoten in D) verbindet.

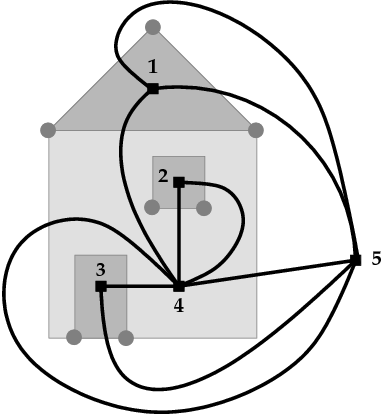
Die folgende Abbildung zeigt einen Graphen (grau) und seinen dualen Graphen (schwarz). Die Knoten des dualen Graphen sind mit Zahlen gekennzeichnet und entsprechen den Regionen des Originalgraphen. Jeder (grauen) Kante des Originalgraphen entspricht eine (schwarze) Kante des dualen Graphen.

Für duale Graphen gilt: Wenn der Originalgraph zusammenhängend ist, enthält jede Region des dualen Graphen genau einen Knoten des Originalgraphen. Deshalb ist der duale Graph des dualen Graphen wieder der Originalgraph. Bei nicht-zusammenhängenden Graphen gilt dies nicht (vgl. das Fenster bei obigem Bild). In diesem Fall hat der duale Graph mehrere mögliche Einbettungen in die Ebene (man kann z.B. die rechte Kante zwischen Knoten 2 und 4 auch links vom Fenster einzeichnen), und man erhält nicht notwendigerweise den Originalgraphen, wenn man den dualen Graphen des dualen berechnet.

Baum

Ein Baum ist ein zusammenhängender, kreisfreier Graph.

Beispiel: Binärer Suchbaum

Spannbaum

Ein Spannbaum eines zusammenhängenden Graphen G ist ein zusammenhängender, kreisfreier Teilgraph von G, der alle Knoten von G enthält

Beispiel: Spannbaum für das "Haus des Nikolaus"

   O   
  /       
 O    O
 |  /  
 | /   
 O----O

Der Spannbaum eines Graphen mit |V| Knoten hat stets |V| - 1 Kanten.

Wald

Ein Wald ist ein unzusammenhängender, kreisfreier Graph.

Jede Zusammenhangskomponente eines Waldes ist ein Baum.

Repräsentation von Graphen

Sei G = ( V, E ) gegeben und liege V in einer linearen Sortierung vor.

<math>V = \{ v_1, ...., v_n \}</math>

Adjazenzmatrix

Ein Graph kann durch eine Adjazenzmatrix repräsentiert werden, die soviele Zeilen und Spalten enthält, wie der Graph Knoten hat. Die Elemente der Adjazenzmatrix sind "1", falls eine Kante zwischen den zugehörigen Knoten existiert:

<math>\mathrm{\bold A} = a_{ij} =

\begin{cases} 1 & \mathrm{falls}\quad (v_i, v_j) \in E \\ 0 & \mathrm{sonst} \end{cases} </math>

Die Indizes der Matrix entsprechen also den Indizes der Knoten gemäß der gegebenen Sortierung. Im Falle eines ungerichteten Graphen ist die Adjazenzmatrix stets symmetrisch (d.h. es gilt <math>a_{ij}=a_{ji}</math>), bei einem gerichteten Graphen ist sie im allgemeinen unsymmetrisch.

Beispiel für einen ungerichteten Graphen:

v = { a,b,c,d }     b      d
                    | \  / |
                    |  \/  |
                    |  /\  |
                    | /  \ |
                    a      c

      a b c d
     -----------
     (0 1 0 1) |a 
 A = (1 0 1 0) |b
     (0 1 0 1) |c
     (1 0 1 0) |d

Die Adjazenzmatrixdarstellung eignet sich besonders für dichte Graphen (d.h. wenn die Zahl der Kanten in O(|V|²) ist.

Adjazenzlisten

In der Adjazenzlistendarstellung wird der Graph als Liste von Knoten repräsentiert, die für jeden Knoten einen Eintrag enthält. Der Eintrag für jeden Knoten ist wiederum eine Liste, die die Nachbarknoten dieses Knotens enthält:

• graph = {adjazencyList(v) | v ∈ V}
• adjazencyList(v) = {v' ∈ V | (v, v') ∈ E}

In Python implementieren wir Adjazenzlisten zweckmäßig als Array von Arrays:

                  graph = [[...],[...],...,[...]]
Adjazenzliste für Knoten =>  0     1         n

Wenn wir bei dem Graphen oben die Knoten wie bei der Adjazenzmatrix indizieren (also a => 0, b => 1, c => 2, d => 3), erhalten wir die Adjazenzlistendarstellung:

graph = [[b, d], [a, c],[b, d], [a, c]]

Auf die Nachbarknoten eines durch seinen Index node gegebenen Knotens können wir also wie folgt zugreifen:

     for neighbors in graph[node]:
         ... # do something with neighbor

Die Adjazenzlistendarstellung ist effizienter, wenn der Graph nicht dicht ist, so dass viele Einträge der Adjazenzmatrix Null wären.

Transponierter Graph

Den transponierten Graphen G^T eines gerichteten Graphen G erhält man, wenn man alle Kantenrichtungen umkehrt.

Bei ungerichteten Graphen hat die Transposition offensichtlich keinen Effekt, weil alle Kanten bereits in beiden Richtungen vorhanden sind, so dass G^T = G gilt. Bei gerichteten Graphen ist die Transposition dann einfach, wenn der Graph als Adjazenzmatrix implementiert ist, weil man einfach die transponierte Adjazenzmatrix verwenden muss (beachte, dass sich die Reihenfolge der Indizes umkehrt):

A^T = a_ji

Ist der Graph hingegen durch eine Adjazenzliste repräsentiert, muss etwas mehr Aufwand getrieben werden:

def transpose(graph):
     gt = [[] for k in graph]   # zunächst leere Adjazenzlisten von GT
     for node in range(len(graph)):
          for neighbor in graph[node]:
              gt[neighbor].append(node)  # füge die umgekehrte Kante in GT ein
     return gt

Durchlaufen von Graphen

Tiefensuche in Graphen

Sei der Graph gegeben als Liste von Listen = g

def dfs (g,node,v=0):
  if v == 0:
    v = [0]*len(g) #visited-Liste
  v[node] = 1 #besuche node
  for t in g[node]: #gehe zu allen Nachbarn
    if v[t] == 0: #falls diese noch nicht besucht
      dfs(g,t,v) #Rekursion

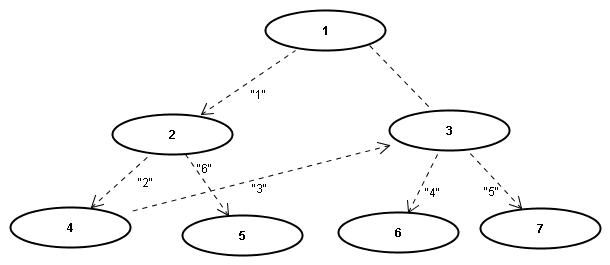
Aufruf dfs(g,1)

=>Folge 1,2,4,3,6,7,5

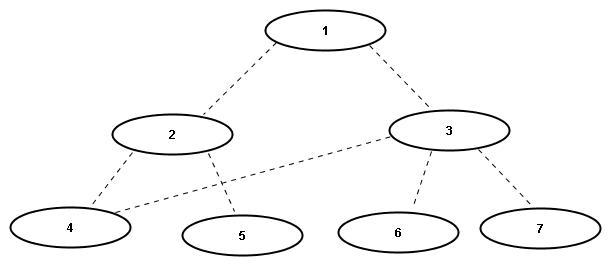
Breitensuche

from Queue import *
def bfs(g,startnode)
  v = [0]*len(g)
  q = Queue()
  v[startnode] = 1 #besuche
  q.put(startnode) #in Schlange
  while not q.empty():
    node = q.get()
    for t in g[node]: 
      if v[t] == 0:
        v[t] = 1
        q.put(t)

Aufgrund von Problemen mit der Implementation von Queue eine neue Version:

def bfs(g,startnode)
  v = [0]*len(g)
  q = []
  v[startnode] = 1 #besuche
  q.append(startnode) #in Schlange
  while not len(q):
    node = q.pop(0)
    for t in g[node]:
      if v[t] == 0:
        v[t] = 1
        q.append(t)

=>Folge 1,2,3,4,5,6,7

Damenproblem

 ---------------
|   | X |   |   |
|---|---|---|---| 
|   |   |   | X |
|---|---|---|---|
| X |   |   |   |
|---|---|---|---|
|   |   |   | X |
 ---------------

4 Damen auf einem vereinfachten Schachbrett so Positionieren, dass sich keine bedroht.

erster Durchlauf:

zweiter Durchlauf:

Weitere Anwendungen (18.06.08)

def dfs(graph):
       '''
       Diese Tiefensuche tut so noch nichts weiter als zu traversieren
       + graph ist Array,
           i-ter Eintrag enthaelt Adjazenzliste (auch Array) des i-ten Knotens,
           wobei Knoten nummeriert von 0 ... v-i
       '''
       def visit(graph, node, visited):
               '''
               visited ist Array mit Flags fuer besuchte Knoten
               '''
               if visited[node]: return
               visited[node] = True
               for neighbor in graph[node]:
                       visit(graph, neighbor, visited)
       visited = [False]*len(graph)
       for node in range(len(graph)):
               visit(graph, node, visited)

Finden von Zusammenhangskomponenten

Ein möglicher Einsatz des Verfahrens ist das Finden von Zusammenhangskomponenten (connected components).

• Beispiel: ...

• Definition: CC_i = {u_k, u_l e V: es gibt einen Pfad von u_k nach u_l ("u_l ist von u_k aus erreichbar")
• für gerichtete Graphen gilt zusätzlich: es gibt einen Pfad von u_l nach u_k}

Die Relation CC_i, also die Zusammenhangskomponenten (ZK) bilden eine Aequivalenzrelation, also kann fuer jede ZK ein Repraesentant bestimmt werden (der sog. "Anker"). Kennt jeder Knoten seinen Anker, so ist das ZK-Problem geloest.

Tiefensuchen-Algorithmus

Unser erster Ansatz ist, den Anker mit Hilfe der Tiefensuche zu finden, wobei statt Knotenbesuche Knotennummern fuer die schon gefundenen Anker gesetzt werden. Ein moeglicher Algorithmus lautet damit wie folgt:

def connectedComponents(graph):
       def visit(graph, node, anchors, anchor):
               '''
               anchor ist Anker der aktuellen ZK
               '''
               if anchors[node] is not None: return # Anker von <node> schon bekannt
               anchors[node] = anchor
               for neighbor in graph[node]
                       visit(graph, neighbor, anchors, anchor)
       
       anchors = [None]*len(graph)
       for node in range(len(graph)):
               visit(graph, node, anchors, node) # node: Anker der naechste ZK = erster Knoten der ZK
       return anchors

• Beispiel: ...

Union-Find-Algorithmus

Eine Alternative (ohne Tiefensuche) waere z.B. ein Union-Find-Algorithmus. Idee dabei ist, dass eingangs jeder Knoten eine eigene ZK bildet, wobei in einer anschliessenden Rekursion Kanten gesucht werden, die zwischen den ZK bestehen.

Initialisierung: jeder Knoten wird als 1 ZK behandelt Rekursion: fasse ZK zusammen (Union) falls Kante zwischen ihnen existiert Ergebnis: Array mit dem Anker jedes Knotens

def unionFindCC(graph):
       def findAnchor(anchors, k):
               '''
               #Prueft auf anchors[k]==k
               '''
               while anchors[k] != k:
                       k = anchors[k]
               return k

       def edges(graph):
               e = []
               for node in range(len(graph)):
                       for n in graph[node]:
                               if node < n:
                                       e.append((node, n))
               return e

       anchors = range(len(graph)) # jeder Knoten ist sein eigener Anker
       for edge in edges(graph):
               # diese Schleife ordnet die Anker so, dass
               #   der 1. Anker immer der kleinste ist
               a1, a2 = findAnchor(anchors, edge[0]), findAnchor(anchors, edge[1])
               if a2 < a1: a2,a1 = a1,a2
               if a1 != a2: anchors[a2] = a1
       for node in range(len(graph)):
               # diese Schleife raeumt mit Indirektionen auf (s. Bsp. (#))
               anchors[node] = findAnchor(anchors, node)
       return anchors

• Beispiel (#): ...

Eine verbreitete Anwendung fuer dieses Verfahren gibt es in der Bildverarbeitung:

• Beispiel: ...

Variationen der Tiefensuche (19.06.2008)

Wichtige Algorithmen, die in der Vorlesung nicht behandelt werden

• Max Flow (zur Bestimmung des maximalen Flusses durch ein Netzwerk, z.B. bei Ölpipelines)
• Matching (auch Paarung genannt): Teilmenge der Kanten eines Graphen, wobei keine zwei Kanten einen gleichen Knoten besitzen

  Anwendungsbereiche: Zuordnung von Gruppen, z.B. Arbeitsamt (Zuordnung Arbeitssuchender - Stellenangebot), Universität (Zuordnung Studenten - Übungsgruppen)

Vereinfachte Lösung für den acyclic-Algorithmus

Zum Finden von Zyklen, bzw. der Feststellung, ob ein Graph azyklisch ist, verwenden wir wieder eine modifizierte Version der Tiefensuche: Die Knoten werden wieder nach dem System der Tiefensuche besucht, und alle besuchten Knoten in einem Array visited abgespeichert. Es gibt einen Zyklus genau dann, wenn man zu einem früheren Knoten (außer zum direkten Vorgaenger) zurückkommt.

  
    def acyclic(graph):
        def visit(graph, node, fromNode, visited):
            if visited[node]:			# Zyklus entdeckt
                return False
            visited[node] = True
            for neighbor in graph[node]:
                if neighbor == fromNode:	# überspringe Nachbar, von dem du gekommen bist
                    continue
                if not visit(graph, neighbor, node, visited):
                    return False		# der Graph ist zyklisch
            return True			# kein Zyklus
        visited = [False]*len(graph)
        for node in range(len(graph)):
            if visited[node]:	# schließt aus, dass Knoten besucht wird, der schon besucht war
                continue
            if not visit(graph, node, None, visited):
                return False
        return True
  

Anmerkungen zum Code:

• Wenn ein Knoten bereits besucht ist, dann gehört er zur gleichen Zusammenhangskomponente - dies hat allerdings nichts mit einem Zyklus zu tun.
• Ein Graph der einmal zyklisch war wird nie wieder azyklisch.
• Der obige Algorithmus weist Ähnlichkeiten mit den bereits behandelten Algorithmen auf: ein guter Algorithmus zeichnet sich dadurch aus, dass mit kleinen Code-Variationen ganz andere Probleme gelöst werden können.

Kürzeste Wege (Pfade)

• Definition: gewichteter Graph

Jeder Kante e ist eine reelle oder natürliche Zahl we zugeordnet (wird auch als
Kantengewicht bezeichnet).

z.B.

• Abstand der Anfangs- und Endknoten

• Durchflusskapazität eines Rohres (für max-Flussprobleme)

• Wechselkurse (Darstellung in einem gerichteten Graph, da jede Kante auch eine Richtung hat. Die Knoten sind die Währungen, die Kanten sind die Wechselkurse. Auf diese Weise lassen sich unterschiedliche Wechselkurse + Bankgebühren darstellen.)

• Definition: Problem des kürzesten Weges

Sei P die Menge aller Wege von u nach v

Puv = {u_v}

und der Weg gegeben durch

u → x1 → x2 → ... → v

dann sind die Kosten eines Weges definiert durch

Kosten (Puv) = <math>\sum\limits_{l \in Pv}</math> we

• gesucht: Pfad u_v, so dass Kosten (u_v) minimal sind

• Lösung: Algorithmus von Dijkstra

Algorithmus von Dijkstra

Edsger Wybe Dijkstra

geb. 11. Mai 1930 in Rotterdam

ges. 06. August 2002

Dijkstra war ein niederländischer Informatiker und Wegbereiter der strukturierten Programmierung. 1972 erhielt er für seine Leistung in der Technik und Kunst der Programmiersprachen den Turing Award, der jährlich von der Association for Computing Machinery (ACM) an Personen verliehen wird, die sich besonders um die Entwicklung der Informatik verdient gemacht haben. Zu seinen Beiträgen zur Informatik gehören unter anderem der Dijkstra-Algorithmus zur Berechnung des kürzesten Weges in einem Graphen sowie eine Abhandlung über den go-to-Befehl und warum er nicht benutzt werden sollte. Der go-to-Befehl war in den 60er und 70er Jahren weit verbreitet, führte aber zu Spaghetti-Code. In seinem berühmten Paper "A Case against the GO TO Statement"[2], das als Brief mit dem Titel "Go-to statement considered harmful" veröffentlicht wurde, argumentiert Dijkstra, dass es umso schwieriger ist, dem Quellcode eines Programmes zu folgen, je mehr go-to-Befehle darin enthalten sind und zeigt, dass man auch ohne diesen Befehl gute Programme schreiben kann.

Algorithmus

 
   import heapq	# heapq ist ein Modul von Python
   def dijkstra(graph, start, ziel):	# graph: gewichtete Adjazenzliste
       heap = []
       visited = [None]*len(graph)
       visited[start] = start
       for neighbor in graph[start]:
           heapq.heappush(heap, (neighbor[1], start, neighbor[0])) # neighbor[1]:Kantengewicht,neighbor[0]:Endpunkt d. K.
       while len(heap) > 0:	# solange der heap nicht leer ist
           w, fromNode, node = heapq.heappop(heap)
           if visited[node] is not None:	# wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
               continue
           visited[node] = fromNode    # baue Vorgänger-Baum
           if node == ziel:	# da der heap noch nicht leer ist, wird an dieser Stelle ein break benötigt
               break
           for neighbor in graph[node]:
               if visited[neighbor[0]] is not None:	# wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
                   continue
               heapq.heappush(heap, (neighbor[1]+w, node, neighbor[0]))
       bestPath = []
       t = ziel
       while t != visited[t]:		# Array wird durchlaufen bis der Anker des Pfades gefunden ist, vgl. Union-Search
           bestPath.append(t)
           t=visited[t]
       bestPath.append(start)
       return bestPath			# bestPath.reverse()
 

Anmerkungen zum Code:

• der graph ist eine gewichtete Adjazenzliste

Knoten	0	→	Endknoten	→	Endknoten	(Nr. der Nachbarn des Knoten 0)
	1		Gewicht		Gewicht	(Gewicht der jeweiligen Kante)
	2
	3

• Eingabe z.B.:

Knoten	0	→	(1, 0.3)	(3, 0.1)	(5, 1.2)
	1	→
	2
	3
	4
	5
	6

• heapq() verwendet den 1. Eintrag des Tupels zum sortieren des heap

Prinzip des Dijkstra-Algorithmus

• Algorithmus ist Tiefensuche mit Prioritätswarteschlange (Heap) statt eines Stapelspeichers (Stack) → vgl. Übung 8

• Die Prioritätswarteschlange speichert die kürzesten Wege, die bereits gefunden worden sind.

• Wenn man die Prioritätswarteschlange (Heap) durch eine Warteschlange (Queue) ersetzt, erhält man Breitensuche.

• Wenn man die Prioritätswarteschlange (Heap) durch einen Stapelspeicher (Stack) ersetzt, erhält man Tiefensuche.

Beispiel

• An der Stelle "neighbor[1]" wird eine Zählvariable count eingefügt, die hoch (Breitensuche) oder runter (Tiefensuche) zählt.

• Die Gewichte werden hoch- oder runtergezählt, so wie die Kanten gesehen wurden.

• Wenn man rückwärts zählt (von 0 abziehen), werden die zuletzt hinzugefügten Kanten expandiert.

• Algorithmus von Dijkstra funktioniert nur für positive Kantengewichte

  <math>\forall</math> w_e > 0

• Bei negativen Kantengewichten könnte es Zyklen geben, die negative Kosten für den ganzen Zyklus haben:

    /\		1. Durchlauf: Kosten -1
 1 /  \ -4	2. Durchlauf: Kosten -2
  /____\	etc.
     2

• Verwendung bei arbitragen Geschäften (Börsengeschäfte, die die Preis-, Kurs- und Zinsunterschiede auf verschiedenen Märkten ausnutzen):

  EURO wurden in YEN, YEN in DOLLAR gewechselt und das Geld hat sich dadurch vermehrt

• Für negative Kantengewichte verwendet man den Bellman-Ford-Allgorithmus, der allerdings langsamer ist, als der Dijkstra-Algorithmus.

Komplexität von Dijkstra

• Jeder Knoten wird höchstens 1x expandiert (Iteration über die Nachbarn des Knotens).

• Jeder Knoten kann mehrmals im Heap enthalten sein.

• Es sind aber höchstens E (Anzahl der Kanten) Heap-Einträge möglich, da jede Kante höchstens 1 Heap-Eintrag generiert (ein Knoten ist nur dann im Heap, wenn man ihn über eine Kante erreicht hat, die man vorher noch nicht besucht hatte). Deshalb können nie mehr Einträge im Heap sein, als es Kanten gibt. Die Komplexität von heappush(), heappop() ist

O(log E) = O(2 log v) = O(log v) 

wenn alle Kanten einen Heap-Eintrag generiert haben.

• Die while-Schleife wird im schlimmsten Fall E mal durchlaufen, deshalb ist die Komplexität von Dijkstra O(E log v).

Korrektheit von Dijkstra

• Falls

visited[node] (Schleifen-Invariante von while) != None 

ist, dann liefert Zurückverfolgen des Pfades von node nach start den kürzesten Pfad von start nach node (gilt für alle Knoten, für die das visited-Feld gesetzt ist).

• Induktionsanfang: visited[start] ist einziger not-None-Fall → Bedingung erfüllt
• Induktionsschritt: wenn visited[node] gesetzt wird, ist es ein kürzester Pfad

Indirekter Beweis

Set S = {node | visited[node] != None} (alle Knoten, von denen wir den kürzesten Pfad schon kennen)

• u ist der Knoten an der Spitze des Heaps
• fromNode <math>\in</math> S (ein Nachbar von node kommt erst dann in den Heap, wenn visited[node] vorher gesetzt wurde)
• falls u → fromNode → start kein kürzester Pfad wäre, müsste u's Vorgänger in V\S sein
• sei dieser Vorgänger x <math>\notin</math> S, x <math>\not=</math> u
• sei w_x das Gewicht der Kante x → u, dann sind die Kosten für start nach u gleich

 Kosten(start_u) = Kosten(start_x) + wx

• Annahme des indirekten Beweises:

 Kosten(start_fromNode) + wfromNode

• Behauptung des indirekten Beweises:

Es gibt einen anderen Pfad x, so dass die Kosten von start nach x geringer sind

• Da aber gilt:

fromNode <math>\in</math> S und x <math>\notin</math> S

• gilt (Induktionsvoraussetzung):

 Kosten(start_fromNode) < Kosten(start_x)

• Falls Kosten(start_x) < Kosten(start_u) müsste x im Heap vor u kommen; daraus folgt, dass u nicht an der Spitze des Heaps sein kann

→ Widerspruch!

→ Die Behauptung, der Weg über x ist besser, kann nicht stimmen.

→ Korrektheit von Dijkstra ist somit bewiesen.

Wie kann man Dijkstra noch verbessern?

A*-Algorithmus

• Verbesserung von Dijkstra im typischen Fall, aber die Komplexität ist immer noch =(Elog v) im schlechtesten Fall (die Komplexität kann man nicht verbessern, aber die Laufzeit im typischen Fall).
• Schätzung für jeden Knoten für den restlichen Weg:

geschätzte Gesamtkosten: Kosten(start_node) + Restschätzung(node_ziel) (exakte Kosten werden durch Dijkstra ermittelt)

Idee:

• Sortiere den Heap nach geschätzten Gesamtkosten.
• Satz:

Falls jede Schätzung den exakten Weg unterschätzt, werden die gleichen Pfade gefunden, wie 
bei Dijkstra (also die korrekten kürzesten Pfade).

(Die Schätzung für den restlichen Weg muss man immer so einrichten, dass der tatsächliche Weg unterschätzt wird. Da keine Straße kürzer sein kann als die Luftlinie, ist die Luftlinie eine geeignete Annahme für A*.)

• Falls der falsche Pfad im Heap eher an die Spitze kommt als der richtige Pfad, findet der A*-Algorithmus den falschen Pfad.
• Wenn der Pfad zum Ziel an der Spitze des Heap ist, dann wird keine Restschätzung mehr benötigt, denn wenn der Zielknoten aus dem Heap herrauskommt, dann hat man die exakte Berechnung. Die Restschätzung ist in diesem Fall 0. Wenn die Schätzung zu klein ist, wird der exakte Weg immer größer sein und zuerst aus dem Heap herauskommen.

Ein minimal aufspannender Baum verbindet alle Punkte eines Graphen bei minimaler Kantenlänge (Quelle)

Minimaler Spannbaum

(engl.: minimum spanning tree; abgekürzt: MST)

gegeben: gewichteter Graph, zusammenhängend

gesucht: Untermenge <math>E'\subseteq E</math>, so dass <math>\sum_{e\in E} w_e</math> minimal und G' zusammenhängend ist.

• G'definiert dann einen Baum, denn andernfalls könnte man <math>\sum_{E'}</math>verringern (eine Kante weglassen) ohne die Zusammenhangskomponente zu verletzen.
  

• Wenn der Graph nicht zusammenhängend ist, würde man den Spannbaum für jede Zusammenhangskomponente getrennt ausrechnen.
• Der MST ist ähnlich wie der Dijkstra-Algorithmus: Dort ist ein Pfad gesucht bei dem die Summe der Gewicht über den Pfad minimal ist.
• Beim MST suchen wir eine Lösung bei der die Summe der Gewichte über den ganzen Graphen minimal ist.

• Das Problem des MST ist nahe verwandt mit der Bestimmung der Zusammenhangskomponente, z.B. über den Tiefensuchbaum, wobei ein beliebiger Baum für die Zusammenhangskomponente und beim MST ein minimaler Baum gesucht ist.

Anwendungen

• Wie verbindet man n Punkte mit möglichst wenigen (kurzen) Straßen (Eisenbahnen, Drähten (bei Schaltungen) usw.)?

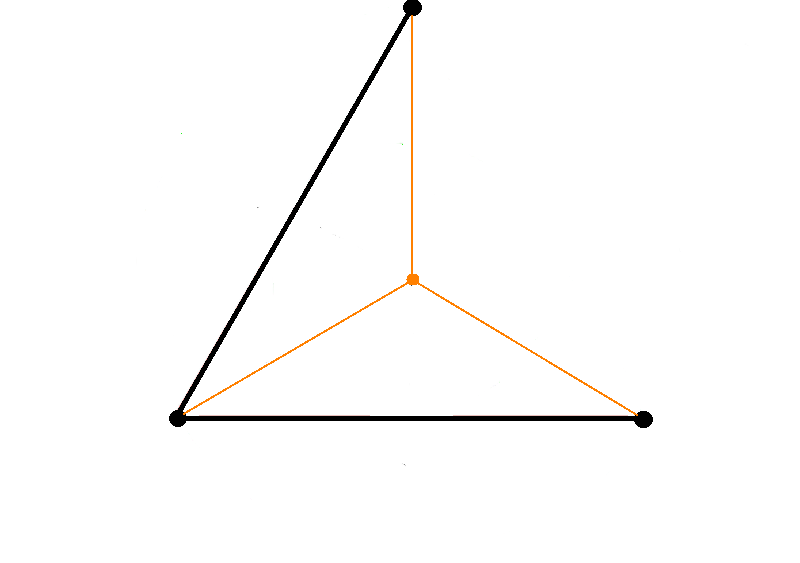
MST minimale Verbindung (Abb.1)	MST = 2 (Länge = Kantengewicht)(Abb.2)

• In der Praxis: Die Festlegung, dass man nur die gegebenen Punkte verwenden darf, ist eine ziemliche starke Einschränkung.

• Wenn man sich vorstellt, es sind drei Punkte gegeben, die als gleichseitiges Dreieck angeordnet sind, dann ist der MST (siehe Abb.2, schwarz gezeichnet) und hat die Länge 2. Man kann hier die Länge als Kantengewicht verwenden.

• Wenn es erlaubt ist zusätzliche Punkte einzufügen, dann kann man in der Mitte einen neuen Punkt setzen <math>\rightarrow</math> neuer MST (siehe Abb.2, orange gezeichnet).
  

• Höhe = <math>\frac{1}{2}\sqrt{3}</math>, Schwerpunkt: teilt die Höhe des Dreiecks im Verhältnis 2:1; der Abstand von obersten Punkt bis zum neu eingeführten Punkt: <math>\frac{2}{3}h = \frac{\sqrt{3}}{3}</math>, davon insgesamt 3 Stück, damit (gilt für den MST in orange eingezeichnet): MST = <math>3\left(\frac{1}{3}\right) \sqrt{3} = \sqrt{3} \approx 1,7</math><br\>

• Damit ist der MST in orange kürzer als der schwarz gezeichnete MST. <br\>

<math>\Rightarrow</math>Folgerung: MST kann kürzer werden, wenn man einen Punkt dazu nimmt.

• Umgekehrt kann der MST auch kürzer werden, wenn man einen Punkt aus dem Graphen entfernt, aber wie das Beipiel des gleichseitigen Dreiecks zeigt, ist dies nicht immer der Fall.

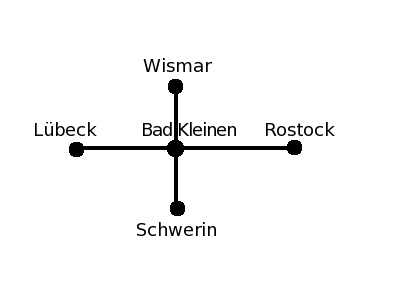
• Methode der zusätzlichen Punkteinfügung hat man früher beim Bahnstreckenbau verwendet. Durch Einführung eines Knotenpunktes kann die Streckenlänge verkürzt werden (Dreiecksungleichung).

• Bestimmung von Datenclustern

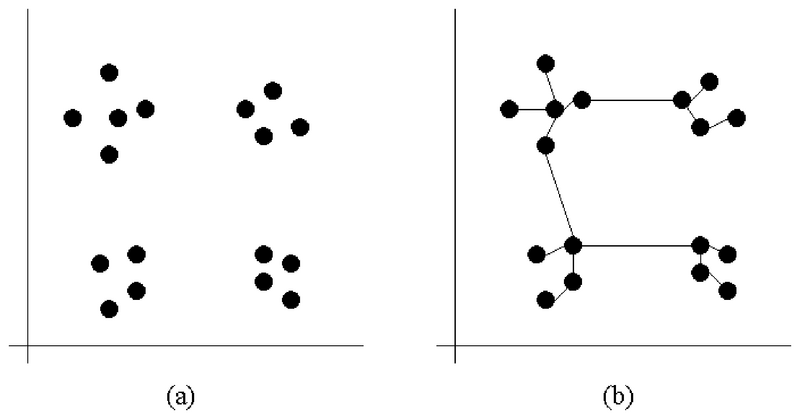
• Daten (in der Abb.: Punkte) bilden Gruppen.

• In der Abbildung hat man 2 verschiedene Messungen gemacht (als x- und y-Achse aufgetragen), bspw. Größe und Gewicht von Personen. Für jede Person i wird ein Punkt an der Koordinate (Größe_i, Gewicht_i) gezeichnet (siehe Bild a). Dies bezeichnet man als Scatter Plot. Wenn bestimmte Wertkombinationen häufiger auftreten als andere, bilden sich mitunter Gruppen aus, bspw. eine Gruppe für "klein und schwer" etc.

• Durch Verbinden der Punkte mittels eines MST (siehe Abbildung (b)) sieht man, dass es kurze (innerhalb der Gruppen) und lange Kanten (zwischen den Gruppen) gibt.

• Wenn man geschickt eine Schwelle einführt und alle Kanten löscht, die länger sind als die Schwelle, dann bekommt man als Zusammenhangskomponente die einzelnen Gruppen.

Zwei Algorithmen für dieses Problem (im Vergleich zu Algorithmen für die Zusammenhangskomponente nur leicht verbesserte Algorithmen)

Algorithmus von Prim

Wikipedia (de) (en)

Idee: starte an der Wurzel (willkürlich gewählter Knoten) und füge jeweils die günstigste Kante hinzu (<math>\rightarrow</math> genau wie beim Dijsktra-Algorithmus, aber die Definitionen, welche Kante die günstigste ist, unterscheiden sich.)

import heapq
def prim(graph):  #Graphdatenstruktur ist wie bei Dijsktra  
	heap = []                                       
	visited = [False]*len(graph) 
	sum = 0  #wird später das Gewicht des Spannbaums sein
	r = []  #r ist die Lösung
	visited[0] = True #fixed
	for neighbor in graph[0]:  #willkürlich 0 als Wurzel gewählt
		heapq.heappush(heap, (neighbor[1], 0, neighbor[0]))  #Heap wird gefüllt 
	while len(heap):
		wn, start, ziel = heapq.heappop(heap) 
		if visited[ziel]: continue
		visited[ziel] = True  #wenn visited noch nicht besetzt
		sum += wn  #Addition des Gewichts der aktuellen Kante
		r.append([start, ziel])  #Kante wird an die Lsg. angehängt
		for neighbor in graph[ziel]:
			if visited[neighbor[0]]: continue
			heapq.heappush(heap, (neighbor[1], ziel, neighbor[0]))
	return sum, r

Algorithmus von Kruskal

Wikipedia (de) (en)

Eine andere Vorgehensweise zur Bestimmung des minimalen Spannbaums besteht darin, einfach Kanten nacheinander hinzuzufügen und hierbei bei jedem Schritt die kürzeste Kante zu verwenden, die keinen Zyklus bildet. Anders ausgedrückt: Der Algorithmus beginnt mit N Bäumen; in (N-1) Schritten kombiniert er jeweils zwei Bäume (unter Verwendung der kürzesten möglichen Kante), bis nur noch ein Baum übrig bleibt. Der Algorithmus von J.Kruskal ist seit 1956 bekannt.

• Idee: wie beim Union-Find-Algorithmus für Zusammenhangskomponenten

1. Behandle jeden Knoten als Baum für sich
2. Fasse zwei Bäume zu einem neuen Baum zusammen

• für MST (im Unterschied zu Union-Find): betrachte dazu die Kanten in aufsteigender Reihenfolge der Gewichte

(priority queue; ignoriere Kanten zwischen Knoten, die sich bereits im gleichem Baum befinden, was sich leicht daran erkennen läßt, dass ihre Anker gleich sind)

• Algorithmus eignet sich besser für das Clusteringproblem, da der Schwellwert von vornerein über die Kantenlänge an den Algorithmus übergeben werden kann. Man hört mit dem Vereinigen auf, wenn die Kantenlänge den Schwellwert überschreitet.
• Es kann keine kürzere Kante als der Schwellwert mehr kommen, da die Kanten vorher sortiert worden sind.

Komplexität: gleich wie beim Dijkstra-Algorithmus, weil jede Kante höchstens einmal in den Heap kommt.

• Aufwand für Heap ist max. <math>E</math> Einträge, da jede Kante nur einmal im Heap sein kann, d.h. Heap hat den Aufwand: <math>O\left(E\log E\right)</math>, falls keine Mehrfachkanten vorhanden: <math>v^2 > E</math> und deshalb: log E < 2 log v.
• Daraus folgt, dass das dasselbe ist wie <math>O \left(E\log v\right)</math>

=> geeignet für Übungsaufgabe

Problem des Handlungsreisenden

(engl.: Traveling Salesman Problem; abgekürzt: TSP)<br\> Wikipedia (de) (en)

Optimaler Reiseweg eines Handlungsreisenden(Quelle)

• Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden.
• Hierbei soll ein Handlungsreisender nacheinander n Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden.
• Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen.

gegeben: zusammenhängender, gewichteter Graph (oft vollständiger Graph)

gesucht: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\>

auch genannt: kürzester Hamiltonkreis

- durch psychologische Experimente wurde herausgefunden, dass Menschen (in 2D) ungefähr proportionale Zeit zur Anzahl der Knoten brauchen, um einen guten Pfad zu finden, der typischerweise nur <math>\lesssim 5%</math> länger als der optimale Pfad ist<br\>

vorgegeben: Startknoten (kann willkürlich gewählt werden), vollständiger Graph

=> v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger...

also <math>\frac{(v-1)!}{2}</math> mögliche Wege in einem vollständigen Graphen

• Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird.
• Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität.

Approximationsalgorithmus

Für viele Probleme in der Praxis sind keine effizienten Algorithmen bekannt (NP-schwer). Diese (z.B. TSP) werden mit Approximationsalgorithmen berechnet, die effizient berechenbar sind, aber nicht unbedingt die optimale Lösung liefern. Beispielsweise ist es relativ einfach, eine Tour zu finden, die höchstens um den Faktor zwei länger ist als die optimale Tour. Die Methode beruht darauf, dass einfach der minimale Spannbaum ermittelt wird.

Approximationsalgorithmus für TSP<br\>

• TSP für n Knoten sei durch Abstandsmatrix D = <math>(d_{ij}) 1 \le i, j \le n</math>

gegeben (vollständiger Graph mit n Knoten, <math>d_{ij}</math> = Kosten der Kante (i,j)) <br\>

gesucht: Rundreise mit minimalen Kosten. Dies ist NP-schwer!<br\>

• D erfüllt die Dreiecksungleichung <math> \Leftrightarrow d_{ij} + d_{jk} \geq d_{ik} \text{ fuer } \forall{i, j, k} \in \lbrace 1, ..., n \rbrace</math> <br\>
• Dies ist insbesondere dann erfüllt, wenn D die Abstände bezüglich einer Metrik darstellt oder D Abschluss einer beliebigen Abstandsmatrix C ist, d.h. :<math>d_{ij}</math> = Länge des kürzesten Weges (bzgl. C) von i nach j.

• Die ”Qualität”der Lösung mit einem Approximationsalgorithmus ist höchstens um einen konstanten Faktor schlechter ist als die des Optimums.

Systematisches Erzeugen aller Permutationen

• Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\>
• Trick: interpretiere jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\>
• Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst.

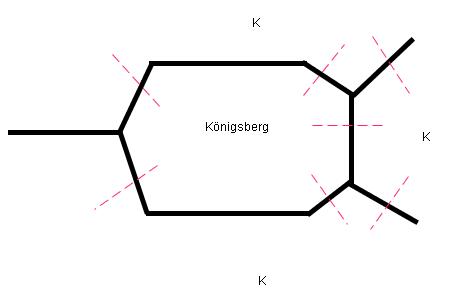
gegeben: zwei Wörter a, b der Länge n=len(a) bzw. m=len(b). Sei k = min(n,m) (im Spezialfall des Vergleichs von Permutationen gilt k = n = m)<br\> Mathematische Definition, wie die Wörter im Wörterbuch sortiert sind: <br\>

<math>a<b \Leftrightarrow

\begin{cases} n < m & \text{ falls fuer } 0 \le i \le k-1 \text{ gilt: } a[i] = b[i] \\ a[j] < b[j] & \text{ falls fuer } 0 \le i \le j-1 \text{ gilt: } a[i] = b[i], \text{ aber fuer ein } j<k: a[j] \ne b[j] \end{cases}</math><br\>

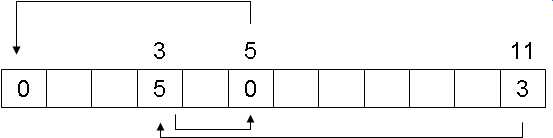
Algorithmus zur Erzeuguung aller Permutationen:

1. beginne mit dem kleinsten Wort bezüglich der lexikographischen Ordnung => das ist das Wort, wo a aufsteigend sortiert ist
2. definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt

Beispiel: Die folgenden Permutationen der Zahlen 1,2,3 sind lexikographisch geordnet

1 2 3    6 Permutationen, da 3! = 6
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
-----
0 1 2 Position

Die lexikographische Ordnung wird deutlicher, wenn wir statt dessen die Buchstaben a,b,c verwenden:

abc
acb
bac
bca
cab
cba

Eine Funktion, die aus einer gegebenen Permutation die in lexikographischer Ordnung nächst folgende erzeugt, kann wie folgt implementiert werden:

def next_permutation(a):
	i = len(a) -1  #letztes Element; man arbeitet sich von hinten nach vorne durch
	while True:  # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird
		if i <= 0: return False  # a ist letzte Permutation
		i -= 1
		if a[i]<a[i+1]: break
	#lexikogr. Nachfolger hat größeres a[i]
	j = len(a)
	while True:
		j -= 1
		if a[i] < a[j]: break
	a[i], a[j] = a[j], a[i] #swap a[i], a[j]
	#sortiere aufsteigend zwischen a[i] und Ende
	#zur Zeit absteigend sortiert => invertieren
	i += 1
	j = len(a) -1
	while i < j:
		a[i], a[j] = a[j], a[i]
		i += 1
		j-= 1
	return True  # eine weitere Permutation gefunden
 	
 def naiveTSP(graph):
	start = 0
	result = range(len(graph))+[start]
	rest = range(1,len(graph))
	c = pathCost(result, graph)
	while next_permutation(rest):
		r = [start]+rest+[start]
		cc = pathCost(r, graph)
		if cc < c:
			c = cc
			result = r
		return c, result

Komplexität: <math>(v-1)!</math> Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also <math>O(v!) = O(v^v)</math>

Beispiel

i = 0			j = 3
↓			↓
1	4	3	2	#input für next_permutation
	i = 2		j = 3
	↓		↓
2	4	3	1	# vertauschen der beiden Elemente
		i = 2
		j = 2
		↓
2	1	3	4	#absteigend sortiert

Stirling'sche Formel

Wikipedia (de) (en)

Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Stirling'sche Formel z.T. starke Vereinfachungen erzielen. <math>v! \approx \sqrt{2 \pi v} \left(\frac{v}{e}\right)^v</math>

<math>O(v!) = O\left(\sqrt{v}\left(\frac{v}{e}\right)^v\right) \approx O(v^v)</math>

Erfüllbarkeitsproblem

geg.:

• n Boolsche Variablen <math>x_i \in \{True,False\}</math> und deren Negation <math>\neg x_i (i=1..n)</math>
• Logischer Ausdruck in <math>x_i,\neg x_i</math>
  • zB <math>(x_1 \vee x_2) \wedge (x_3 \vee x_4)</math> ...

   Grammatik eines logischen Ausdrucks(in BNF):
   <EXP>  ::= <DISJ>
   <DISJ> ::= <CONJ> | <DISJ> <math>\vee</math> <CONJ>
   <CONJ> ::= <TERM> | <CONJ> <math>\wedge</math> <TERM>
   <TERM> ::= ( <EXPR> ) | ¬( <EXPR> ) | <VAR> | ¬<VAR>
   <VAR>  ::= <math>x_1</math> | ... | <math>x_n</math>

ges.: Eine Belegung der <math>x_i</math>, so dass der gegebene Ausdruck "True" wird

Naive Lösung

Probiere alle Bedingungen aus <math>\to</math> Komplexität <math>\mathcal{O}(2^{n}) \!</math>
Im Allgemeinen ist das der effizienteste bekannte Algorithmus

Normalformen von logischen Ausdrücken

k-Konjunktionen-Normalform(k-CNF)

• ein "Literal" ist eine Variable <math>x_i</math> oder deren Negation
• jeweils k Literale werden mit <math>\vee</math> in einer Disjunktion verknüpft
• Disjunktionen werden mit <math>\wedge</math> in einer Konjunktion verbunden

   Grammatik eines Ausdrucks in k-CNF(wieder in BNF):
   <EXP>  ::= <CONJ>
   <CONJ> ::= <DISJ> | <CONJ> <math>\wedge</math> <DISJ>
   <DISJ> ::= ( <LIT> <math>\vee</math> ... <math>\vee</math> <LIT> ) <!-- k Literale -->
   <LIT>  ::=  <VAR> | <math>\neg</math><VAR> 
   <VAR>  ::= <math>x_1</math> | ... | <math>x_n</math> 

Beispiele:

• 3-CNF: <math>(x_1 \vee \neg x_2 \vee x_4) \wedge (x_2 \vee x_3 \vee \neg x_4) \wedge (\neg x_1 \vee x_4 \vee \neg x_5)</math>
• 2-CNF: <math>(x_1 \vee \neg x_2) \wedge (x_3 \vee x_4)</math> ...

Satz:

• Jeder logische Ausdruck kann in polynomieller Zeit in 3-CNF umgewandelt werden
• Im Allgemeinen kann ein logischer Ausdruck nicht in 2-CNF umgeschrieben werden

Implikationen-Normalform(INF)

Konjunktionen von Implikationen:

• zB <math>(x_1 \to x_2) \wedge (x_2 \to \neg x_3) \wedge (x_4 \to x_3)</math>

   Grammatik eines Ausdrucks in INF(you know the drill ;)):
   <EXP>  ::= <CONJ>
   <CONJ> ::= <IMPL> | <CONJ> <math>\wedge</math> <IMPL>
   <IMPL> ::= ( <LIT> <math>\to</math> <LIT> )
   <LIT>  ::=  <VAR> | <math>\neg</math><VAR> 
   <VAR>  ::= <math>x_1</math> | ... | <math>x_n</math> 

Satz:

• jeder Ausdruck in 2-CNF kann in INF umgewandelt werden (siehe z.B. hier):

  <math> (x_i \vee x_j) \Leftrightarrow (\neg x_i \to x_j) \wedge (\neg x_j \to x_i) </math>

Außerdem kann jeder Ausdruck in INF als gerichteter Graph dargestellt werden

1. Jede Variable und ihre Negation sind 1 Knoten(dh insgesamt 2 Knoten)
2. Jede Implikation ist eine gerichtete Kante

Stark zusammenhängende Komponenten

geg.: gerichteter Graph

   1. Bestimme die post Order Time (mit Tiefensuche)
   2. Transponieren des Graphen <math>G^T</math>
   3. Bestimme ConnComp <math>G^T</math> mit bekannten CC Algorithmen, aber so, dass Knoten in absteigender post Order behandelt werden

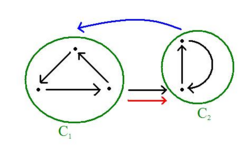
Beweis: 1.Bilde Komponentengraphen:

   Knoten: jede SCC <math>C_i</math> ist ein Knoten
   Kanten: <math>C_i \rightarrow C_j \Leftrightarrow U_k \rightarrow U_l</math> mit <math>U_k \in C_i</math> und <math>U_l \in C_j</math>

   *Eigenschaft 1: der Komponentengraph ist :azyklisch:
    <math>pot \left(C_i\right) = max_{U_k \in C_i}  pot\left(U_k\right)</math>
   
   *Eigenschaft 2: falls <math>C_i \rightsquigarrow C_j</math> dann <math>pot \left(C_i\right) > pot \left(C_j\right)</math>
    (ausserdem gilt: es gibt keinen Weg <math>C_j \rightsquigarrow C_i</math> )
    aber: in transponierten Graphen sind alle Kanten umgedreht
   
   *Eigenschaft 3: falls <math>{C_j}^T \rightsquigarrow {C_i}^T</math> , dann gilt <math>pot \left({C_i}^T\right) > pot \left({C_j}^T\right)</math>

Eigenschaft 2-3 <math>\Longrightarrow</math> im transponierten Graphen gibt es nie einen Pfad <math>{C_i}^T \rightsquigarrow {C_j}^T</math>

Falls <math>pot \left({C_i}^T\right) > pot \left({C_j}^T\right)</math>

<math>\Longrightarrow</math> Schritt 3 des Algorithmus kann von einem geg. Startknoten nur die Knoten derselben SCC erreichen

q.e.d.

postOrderTime

   ## In einem Baum: besuche erst die Kinder, dann die Wurzel
   def postOrderTime(graph):
       visited = [None] * len(graph) 
       def visit(node, count):
           #markiert, dass 'node' besucht wurde, aber noch nicht fertig ist
           visited[node] = -1
           for  neighbor in graph[node]:
               if visited[neighbor] is not None: continue
               count = visit(neighbor, count)
           visited[node] = count
           count += 1
           return count
       count = 0
       for node in range(len(graph)):
           if visited[node] is not None: continue
           count = visit(node, count)
       return visited

transpose

   ## Kehre die Richtung der Pfeile in einem Graphen um (tut nichts fuer ungerichtete Pfeile und Graphen).
   def transpose(graph):
       grapht = [[] for k in range(len(graph))]
       for node in range(len(graph)):
           for neighbor in graph[node]:
               grapht[neighbor].append(node)
       return grapht

strongCC

   ## Jede Komponente durch e. Ankerknoten repräsentiert
   ## Jedes SCC ist die Menge aller Knoten mit identischem Ankterknoten
   def strongCC(graph):
       # Prinzip: Tiefensuche mit absteigender Post-Order-Time
       postOrder = postOrderTime(graph)
       # ordered = [(knotenindex, POT), ...]
       ordered = zip(range(len(graph)), postOrder)
       ordered.sort(key=lambda x: x[1], reverse=True)
       
       grapht = transpose(graph)
       anchors = [None] * len(graph)
       def visit(node, anchor):
           if anchors[node] is not None: return
           anchors[node] = anchor
           for neighbor in grapht[node]:
               visit(neighbor, anchor)
       
       for node in ordered:
           visit(node[0], node[0])
       return anchors

Anwendung auf 2-SAT Problem

geg.: Implikationen-Normalform, dargestellt als gerichteter Graph.

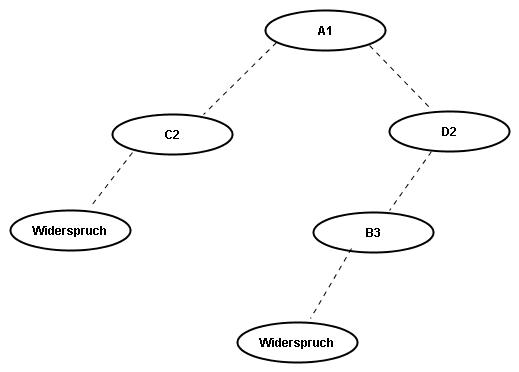
Eigenschaft: alle Variablen in derselben SCC müssen den gleichen Wert haben, weil

<math>\underbrace{x_i \rightsquigarrow x_j \stackrel{\wedge}{=} x_i \rightarrow x_j; \;\;\; x_j \rightsquigarrow x_i \stackrel{\wedge}{=} x_j \rightarrow x_i}</math>

<math>\;\;\;x_i == x_j</math>

<math>\rightarrow \; x_i \; und \; \neg x_i</math> dürfen nie in derselben SCC sein, weil <math>x_i == \neg x_i</math> ein Widerspruch ist

<math>\Longrightarrow</math> Algorithmus für Erfüllbarkeit von INF: teste diese Eigenschaft für jede stark zusammenhängende Komponente des Implikationengraphen

Das funktioniert leider nicht für k-SAT mit <math>k>2</math>

Nächstes Thema