Randomisierte Algorithmen

1. Randomisierte Algorithmen

Def.: Algorithmen, die bei Entscheidung oder bei der Wahl der Parameter Zufallszahlen benutzen

Bsp.: Lösen des K-SAT-Problems durch RA

   geg.: logischer Ausdruck in K-CNF (n Variablen, m Klauseln, k Variablen pro Klausel)

   <math>\underbrace {\underbrace {\left(x_1 \vee x_3 \vee...\right)}_{k\; Variablen} \wedge \left( x_2 \vee x_4 \vee...\right)}_{m\;Klauseln}</math>

   for i in range (trials):    #Anzahl der Versuche
        #Bestimme eine Zufallsbelegung des <math>\{ x_i \}</math>:
        for j in range (steps):
              if <math>\{ x_i \}</math> erfüllt alle Klauseln: return <math>\{ x_i \}</math>
              #wähle zufällig eine Klausel, die nicht erfüllt ist und negiere zufällig eine der Variablen in dieser Klausel 
              (die Klausel ist jetzt erfüllt)
   return None

Eigenschaft: falls <math>k>2</math> : steps *trials <math>\in O\left(\Alpha^n \right) \Alpha >1</math>

z.B. <math>k=3</math> steps=3*n, trials=<math>\left(\frac{4}3\right)^n</math>

aber: bei <math>k=2</math> sind im Mittel nur steps=<math>O\left(n^2\right)</math> nötig, trials=<math>O\left(1\right)</math>

---

-Zufallsbelegung hat <math>t\leq n</math> richtige Variablen (im Mittel <math>t\approx \frac {n} 2</math>)

Negieren einer Variable ändert t um 1, u.Z. <math>t\rightarrow t+1</math> mit Wahrscheinlichkeit <math>\frac 1 2</math> ::(für beliebiges k: <math>\frac 1 k</math>)

<math>t\rightarrow t-1</math> mit Wahrscheinlichkeit <math>\frac 1 2</math> ::(für beliebiges k: <math>\frac {k-1} k</math>)

-Wieviele Schritte braucht man im Mittel, um zu einer Lösung mit t Richtigen zu kommen?

      <math>S\left(t\right)=\frac 1 2 S\left(t-1\right) + \frac 1 2 S\left(t+1\right) +1</math>
      
      <math>S\left(n\right)=0</math>    #Abbruchbedingung der Schleife
      
      <math>S\left(0\right) = S\left( 1\right) + 1 \Longrightarrow S\left(t\right) = n^2-t^2</math>

      Probe: <math>S\left(n\right)=n^2-n^2=0</math> 
                 
             <math>S\left(0\right) =n^2-0^2</math>  
             
                  <math>=S\left(1\right)+1</math>
             
                  <math>\;=n^2-1^2+1</math>
             
                  <math>\;=n^2</math>
             <math>S\left(t\right)=\frac 1 2 \left(n^2-\left(t-1\right)^2\right) + \frac 1 2 \left(n^2-\left(t+1\right)^2\right)+1</math> 
             
                  <math>=\frac 1 2 n^2-\frac 1 2 \left( t^2-2t+1\right) + \frac 1 2 n^2-\frac 1 2</math>
             
                  <math>=\left(t^2+2t+1\right)</math>              
             
                  <math>\;=n^2-t^2</math>

Das ist das Random Walk Problem

Im ungünstigsten Fall (t=0) werden im Mittel <math>n^2</math> Schritte benötigt, um durch random walk nach t=n zu gelangen.

2. RANSAC-ALGORITHMUS (Random Sample Consensus)

Aufgabe: gegeben: Datenpunkte

gesucht: Modell, das die Datenpunkte erklärt

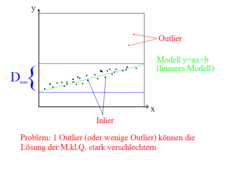
Messpunkte:

     übliche Lösung: Methode der kleinsten Quadrate
     
     <math>\min_{a,b} 	\sum_{i} \left(a x_i + b + y_i\right)^2</math>
     
     Schulmathematik:      <math>Minimum\stackrel{\wedge}{=}Ableitung=0</math>

Lineares Gleichungssystem

<math>\frac{d}{da}\sum{i} \left(ax_i+b-y_i\right)^2=\sum{i} \frac{d}{da} \left[ax_i+b-y_i\right)^2</math>

<math>f\left(g\left(x\right)\right)</math>

<math>f\left(x\right)=x^2</math>

<math>y\left(a\right)=ax_i+b-y_i</math>

<math>=\sum_{i}2\left(ax_i+b-y_i\right)\frac{d}{da} \underbrace {ax_i+b-y_i}_{x_i}</math>

<math>\underline {=2\sum_{i}\left(ax_i+b-y_i\right)x_i\stackrel{!}{=}0}</math>

<math>a\sum_{i}{x_i}^2+b\sum_{i}x_i=\sum_{i}x_iy_i</math>

<math>a\sum_{i}x_i+b\sum_{i}1=\sum_{i}y_i</math>

<math>\frac{d}{db}\sum_{i}\left(ax_i+b-y_i\right)^2=2\sum_{i}\left(ax_i+b-y_i\right)*1</math>

---

Problem: <math>\epsilon  %</math> der Datenpunkte sind Outlier

<math>\Longrightarrow</math> Einfaches Anpassen des Modells an die Datenpunkte funktioniert nicht

Seien mindestens k Datenpunkte notwendig, um das Programm anpassen zu können

RANSAC-Algorithmus

     for  l in range (trials):
          wähle zufällig k Punkte aus
          passe das Modell an die k Punkte an
          zähle, wieviele Punkte in der Nähe des Modells liegen (d.h. <math>d_i < d_max</math> muss geschickt gewählt werden) 
                                          #Bsp. Geradenfinden:-wähle a,b aus zwei Punkten
                                                              -berechne: <math>|ax_i+b-y_i|=d_i</math>
                                                              -zähle Punkt i als Inlier, falls <math>d_i<d_ma</math>
     return: Modell mit höchster Zahl der Inlier

     <math>trials= \frac{log\left(1-p\right)}{log\left(1-\left(1-\epsilon\right)^k\right)}</math>  mit k=Anzahl der Datenpunkte und p=Erfolgswahrscheinlichkeit, <math>\epsilon</math>=Outlier-Anteil

Erfolgswahrscheinlichkeit: p=99%

<math>\begin{array}{|c||c|c|c|c|c|}

        Beispiel & k & \epsilon=10% & 20% & 50% & 70%\\
        \hline
        Linie\;in\;2D & 2 & 3 &5 & 17 & 49\\
        Kreis\;in\;2D & 3 & 4 & 7 & 35 & 169\\
        Ebene\;in\;3D & 8 & 9 & 26 & 1172 & 70188\\
      \end{array}</math>

Ein Spiel: Wie viel Schritte braucht man im Mittel zum Ziel?

  geg.: 5 Plätze, 2 Personen: eine Person rückt vom einem Platz zu dem enderen Platz;
        die zweite Person wirft die Münze.
        Wenn die Münze auf Kopf landet, rücke nach rechts und wenn die Münze auf Zahl landet, rücke nach links.
        <--- Zahl                                                         Kopf-->
        Kopf: /////
        Zahl: /// 

=> mit 8 Schritten bis zum Ziel

im Mittel: bei N Plätzen braucht man N² Schritte

all: mit N² Schritten um N Plätze rücken

Wie viel Schritte braucht man im Mittel zum Ziel?

        <math>S\left(N\right)=0</math>    #wenn wir uns im Stuhl Nr.1 befinden
          
        <math>S\left(i\right)=\frac 1 2 S\left(1 + S\left(i+1\right)\right) + \frac 1 2 S\left(1 + S\left(i-1\right)\right) = \frac 1 2 S\left(i+1\right) + \frac 1 2 S\left(i-1\right) +1 </math>

        <math>S\left(0\right)=1 + S\left(1\right)</math>    #bei 0.Platz

• Lösung:

        <math>S\left(i\right)= N^2 - i^2</math>

• speziell:

        <math>S\left(i\right)= N^2</math>           #wenn man am ungünstigsten Platz startet

---

Beziehung zu randomisiertem 2-SAT

     "Platz <math>i</math> ": <math>i</math> Variablen haben den richtigen Wert,  <math>\left(N-i\right)</math>  sind falsch gesetzt

     <math>S\left(\frac N 2\right)=N^2 - \left(\frac N 2\right)^2 = N^2 - \frac N 4 ^2 = \frac 3 4 N^2 </math>
     <math>S\left(\frac N 2\right)</math>     # Anfangszustand

---

Las Vegas vs. Monte Carlo

  * Las Vegas - Algorithmen
    - Ergebnis ist immer korrekt.
    - Berechnung ist mit hoher Wahrscheinlichkeit effizient (d.h. Randomisierung macht den ungünstigsten Fall unwahrscheinlich).

  * Monte Carlo - Algorithmen
    - Berechnung immer effizient.
    - Ergebnis mit hoher Wahrscheinlichkeit korrekt (falls kein effizienter Algorithmus bekannt, der immer die richtige Lösung liefert).

Las Vegas	Monte Carlo
- Erzeugen einer perfekten Hashfuktion	- Algorithmus von Freiwald(Matrizenmultiplikation)
- universelles Hashing	- RANSAC
- Quick Sort mit zufälliger Wahl des Pivot-Elements	- randomisierte K-SAT(k>=3)(Alg. von Schöning)
- Treep mit zufälligen Prioritäten

Zufallszahlen

- kann man nicht mit deterministischen Computern erzeugen

- aber man kann Pseudo-Zufallszahlen erzeugen, die viele Eigenschaften von echten Zufallszahlen haben

* sehr ähnlich zum Hash

    "linear Conguential Random number generator"
       <math>I_{i+1}= \left(a*I_i + c\right)mod m</math>
       <math>\begin{array}{ll}
       \mathrm{=> } & I_i \in [0, m-1]\\

       \end{array}</math>

-sorgfältige Wahl von a, c, m notwendig