Prioritätswarteschlangen

Definitionen

Prioritätswarteschlangen verwendet man, wenn man in einem Container wiederholt das jeweils kleinste (Min Priority Queue) oder größte (Max Priority Queue) Element finden und gewöhnlich auch aus dem Container entfernen muss. Die typische Schnittstelle einer Prioritätswarteschlange pq enthält also typischerweise folgende effizient implementierte Operationen:

Max Priority Queue

   pq.insert(x)          # Element x einfügen
   x = pq.largest()      # das aktuell größte Element zurückgeben (aber es bleibt in der Queue)
   pq.removeLargest()    # das aktuell größte Element entfernen

Min Priority Queue

   pq.insert(x)          # Element x einfügen
   x = pq.smallest()     # das aktuell kleinste Element zurückgeben (aber es bleibt in der Queue)
   pq.removeSmallest()   # das aktuell kleinste Element entfernen

Die Funktionen insert und remove werden auch oft mit push bzw. pop bezeichnet (wie beim Stack). In vielen Implementationen gibt remove außerdem das aktuelle größte bzw. kleinste Element zurück. Neben Min und Max Queue gibt es auch die bidirektionale Prioritätswarteschlange, die das kleinste und das größte Element effizient finden und entfernen kann.

Prioritätswarteschlange als sequentielles Suchproblem

Am einfachsten kann eine Prioritätswarteschlange durch sequentielle Suche realisiert werden. In diesem Fall ist einfach ein (unsortiertes) dynamisches Array a gegeben, dessen Elemente mit Prioritäten ausgestattet sind. Dann gilt

    pq.insert(x)<=> a.append(x)   (amortisierte Komplexität  <math>\mathcal{O}(1)</math>)

Die Suche (in diesem Fall nach dem Element mit maximaler Priorität) wird durch sequenzielles Durchlaufen des Arrays realisiert

def largest(a):
   N = len(a)
   if N == 0:  
       raise RuntimeError("Access to empty priority queue.")
   max = a[0]
   k = 0
   for n in range(1, N):       # Dieser Code entspricht der inneren Schleife von Selection Sort
       if a[n] > max:          # Die Suche hat also die Komplexität O(N).
           max = a[n]
           k = n
   return k                    # Den Index des kleinsten Elements zurückgeben

Ähnlich implementiert man das Entfernen des größten Elements: Man sucht zunächst dessen Index, schiebt dann alle nachfolgenden Elemente um einen Index nach vorn, und verkürzt schließlich das dynamische Array um ein Element.

Alternativ kann man auch die Komplexität von insert und largest vertauschen: insert kann die Queue sortiert aufbauen (indem jedes neue Element an seinem richtigen Platz eingefügt wird, was einen Aufwand von O(N) verursacht, da man im Mittel N/2 Elemente einen Platz nach hinten verschieben muss), so dass bei largest einfach in O(1) auf das letzte Element des Array zugegriffen wird. Auch das Entfernen des größten, also letzten Elements hat jetzt die amortisierte Komplexität O(1).

Bei kleinen Arrays ist die sequentielle Suche die schnellste Methode. Bei großen Arrays hingegen ist die Suche mit O(N) nicht effizient.

Prioritätssuche mit einem binären (balancierten) Suchbaum

Ein binärer Suchbaum eignet sich offensichtlich für die Prioritätssuche, weil das Einfügen und Entfernen eines Elements sowie die Suche nach dem kleinsten oder größten Element jeweils in <math>\mathcal{O}(\log N)</math> realisiert werden kann, falls der Baum balanciert ist. Man implementiert also insert z.B. wie beim Andersson-Baum. Die Suche nach dem größten Element wird durch eine einfache rekursive Funktion realisiert:

def largest(node):                     # node istr die Wurzel des zu durchsuchenden Teilbaums
     if node.right is not None:        # rechts stehen immer die großen Elemente
         return largest(node.right)    # => Rekursion in den rechten Teilbaum
     return node                       # wenn es nicht mehr nach rechts geht, dann haben wir den größten Knoten gefunden

Diese Funktion hat, wie auch insert und remove, die Komplexität <math>\mathcal{O}(\log N)</math>. Alle Funktionen sind somit für große Datenstrukturen effizient. Allerdings stellt sich heraus, dass die Datenstruktur eines balancierten Suchbaums viel komplizierter ist, als für die Prioritätssuche notwendig wäre.

Heap

Die Datenstruktur des Heap ist speziell für die Prioritätssuche optimiert. Im Unterschied zum Suchbaum sucht man ja nicht nach einem beliebigen Element, sondern stets nach dem größten oder kleinsten. Dadurch kann die Datenstruktur signifikant vereinfacht werden.

Linkslastiger perfekt-balancierter Binärbaum

Ein linkslastiger Binärbaum ist ein Binärbaum, bei dem für jeden Knoten gilt, dass die Tiefe des linken Unterbaumes größer oder gleich der Tiefe des rechten Unterbaumes ist. Ein leerer Unterbaum hat dabei die Tiefe Null.

d(node.left) ≥ d(node.right)

Wenn ein linkslastiger Binärbaum außerdem perfekt balanciert ist, gilt für alle Knoten sogar

1 ≥ d(node.left) - d(node.right) ≥ 0

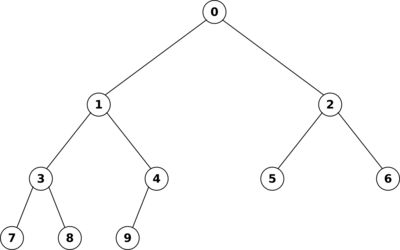
d.h., die Höhe des linken Teilbaums kann maximal um Eins größer sein als die des rechten. Die folgende Graphik zeigt, dass man einen linkslastigen, perfekt balancierter Binärbaum effizient als Array implementieren kann, indem man die Knoten von oben nach unten und von rechts nach links durchnummeriert, und diese Nummern als Array-Indizes verwendet:

Dieser Baum entspricht dem Array

  0, 1, 2, 3, 4, 5, 6, 7, 8, 9

In der Array-Repräsentation kann man den Vater und die Kinder eines gegebenen Knotens index durch einfache Umrechnung der Arrayindizes bestimmen:

   parentIndex     = floor((index - 1)/2)   # floor() heißt abrunden
   leftChildIndex  = 2*index + 1
   rightChildIndex = 2*index + 2

Diese Formeln gelten unter der Voraussetzung, dass die Indexzählung bei Null beginnt. Die Wurzel des Baumes hat also den Index 0. Ein neuer Knoten wird einfach am Ende des Arrays angehängt, und er ist ein linkes Kind, falls sein Index ungerade ist, andernfalls ein rechtes Kind. Offensichtlich bleibt durch diese Einfügestrategie die Eigenschaften der Linkslastigkeit und perfekten Balance erhalten.

Heap-Bedingung

Ein Heap ist ein linkslastiger perfekt-balancierter Binärbaum, für den zusätzlich eine Heap-Bedingung gilt. Ein Baum erfüllt die Max-Heap-Bedingung, wenn für jedem Teilbaum gilt, dass die Wurzel eine höhere Prioriät hat als die Kinder. Entsprechend erfüllt der Baum die Min-Heap-Bedingung, wenn die Wurzel kleinere Priorität hat als die Kinder.

Im Kontext der array-basierten Repräsentation bedeutet dies, dass die Wurzel, also das Element heap[0] die größte (bzw. kleinste) Priorität hat. Die Funktion largest kann somit trivial implementiert werden:

def largest(heap):
    return heap[0]    # Komplexität <math>\mathcal{O}(1)</math>

Einfügen in einem Heap

h - Array #speichrt Haep

 def insert(h,x):

     h.append(x)  # wir speichern den Wurzel am Ende, so wird glecih zu einem linkslastigen perfect balancierten Baum (die Haep - Bedingung ist erfüllt)

     upheap(h, len(h) - 1):

def upheap(h, k):

   """k-tes Element evtl. an der falsche Stelle

   """

   v = h[k]

   while True      #endlose Schleife
        
       if k == 0:

           break

       parent = (k - 1)/2

       if h[parent]>v:

           break

       h[k] = h[parent]

       k = parent

   h[k] = v

def removeLargest(h):
    h[0] = h[len(h) - 1]

    del h[len(n) - 1]              <math>\mathcal{O}(1)</math>

    downHeap(h, 0)                       <math>\mathcal{O}(logN)</math>

def downHeap(h, k):

    v = h[k]

    while True

        child = 2k + 1              #linke Kind

        if child <math>\ge</math>len(h):

              break

        if child < h[child] < h[child + 1]         #rechtes Kind

              child = child + 1
        if v <math>\ge</math> h[child]:

              break

        h[k] = h[child]

        k = child

   h[k] = v

Beispiel am Wort "SORTING"

(Grafiken folgen)

weitere Heapvarianten

• Min-Max-Priority Queue ("Deap", Double Ended Heap)
• Binomialer Heap, effiziente Operation "merege Heap" <math>\mathcal{O}(n * log N (i*N_1 + N_2)</math>

(Beweis durch binomiale Koeffizienten, Zusammenführen zweier Prioritätslisten)

• Fibonacci-Heap, einfügen in amortisierter Zeit <math>\mathcal{O}(1)</math>

(Beweis durch Fibonacci Zahlen)