Graphen und Graphenalgorithmen: Difference between revisions
(→Minimaler Spannbaum: gleichseitiges Dreieck verbessert) |
|||
| Line 3: | Line 3: | ||
=== Motivation === | === Motivation === | ||
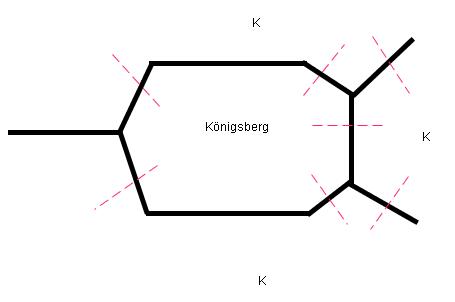
==== Königsberger | ==== Königsberger Brückenproblem ==== | ||
(1736 | (Euler, 1736) | ||
[[Image:Koenigsberg.jpg]] | [[Image:Koenigsberg.jpg]] | ||
| Line 13: | Line 11: | ||
Königsberger Brücken: | Königsberger Brücken: | ||
Spaziergang durch Königsberg, so dass alle Brücken nur einmal überquert werden. | Gesucht ist ein Spaziergang durch Königsberg, so dass alle Brücken nur einmal überquert werden. | ||
Geometrie: | Ein Graph abstrahiert von der Geometrie des Problems und repräsentiert nur die Topologie. Jeder Stadtteil von Königsberg ist ein Knoten des Graphen, jede Brücke eine Kante. Der zum Brückenproblem gehörende Graph sieht also so aus: | ||
O | O | ||
/| \ | |||
\| \ | |||
O | O---O | ||
/| / | |||
\| / | |||
O | O | ||
;Definition -- ungerichteter Graph: Ein ungerichteter Graph G = ( V, E ) besteht aus | |||
:* einer endliche Menge V von Knoten (vertices) | |||
Ein ungerichteter Graph G = ( V, E ) | :* einer endlichen Menge <math>E \subset V \times V</math> von Kanten (edges) | ||
:Ein Graph heißt ungerichtet, wenn zusätzlich gilt: | |||
* | :::(x,y) ∈ E => (y,x) ∈ E (Symmetrie) | ||
* | |||
Ein Graph heißt ungerichtet, wenn zusätzlich gilt: | |||
(x,y) ∈ E => (y,x) ∈ E ( | |||
Bsp: | Bsp: | ||
Revision as of 20:44, 3 July 2008
Einführung zu Graphen
Motivation
Königsberger Brückenproblem
(Euler, 1736)
Königsberger Brücken:
Gesucht ist ein Spaziergang durch Königsberg, so dass alle Brücken nur einmal überquert werden.
Ein Graph abstrahiert von der Geometrie des Problems und repräsentiert nur die Topologie. Jeder Stadtteil von Königsberg ist ein Knoten des Graphen, jede Brücke eine Kante. Der zum Brückenproblem gehörende Graph sieht also so aus:
O
/| \
\| \
O---O
/| /
\| /
O
- Definition -- ungerichteter Graph
- Ein ungerichteter Graph G = ( V, E ) besteht aus
- einer endliche Menge V von Knoten (vertices)
- einer endlichen Menge <math>E \subset V \times V</math> von Kanten (edges)
- Ein Graph heißt ungerichtet, wenn zusätzlich gilt:
- (x,y) ∈ E => (y,x) ∈ E (Symmetrie)
Bsp:
ungerichtet O || \ || \ O O || / || / O
Bsp:
- Landkarten:
- Knoten: Länder
- Kanten: gem. Grenzen
- Schaltkreis:
- Knoten: Gatter
- Kanten: Verbindungen
- Chemie (Summenformeln):
- Knoten: Elemente
- Kanten: Bindungen
- Soziologie (StudieVZ)
- Soziogramm
- Knoten: Personen
- Kanten: Freund von ...
- Soziogramm
- Definition: Vollständige Graphen
Bei vollständigen Graphen ist jeder Knoten mit allen anderen Knoten verbunden.
E = U V (v,w) u (w,v) | v ∈ V, w ∈ V, u != w
 |
 |
 |
 |
 |
Rätsel
Auf einer Party sind Leute. Alle stoßen miteinander an. Es hat 78 mal "Pling" gemacht.
Wieviele Leute waren da?
Repräsentation von Graphen
Sei G = ( V, E ) geg und liege V in einer lineraren Sortierung vor. V = { v1, ...., vn }
Adjazenzmatrix
AG = aij = {1 falls (vi, vj) ∈ E ; sonst 0}
Bsp:
v = { a,b,c,d } b d
| \ / |
| \/ |
| /\ |
| / \ |
a c
a b c d
-----------
(0 1 0 1) |a
AG = (1 0 1 0) |b
(0 1 0 1) |c
(1 0 1 0) |d
Adjezenzlisten
al(v) = {v' ∈ V | (u,u') ∈ E} Lg = ((v1, al(v1)), ...., (vn, al(vn))
Python:
Array von Arrays [[...],[...],...,[...]]
0 1 n
- Definition: Teilgraphen
Ein Graph G' = (v',E') ist ein Teilgraph, wenn gilt:
- v' c V
- E' c E
Er heißt erzegender Graph, wenn zusätzlich gilt:
- v' = V
- Definition: Knotengrade
Für G = (v,E)und v ∈ V grad(v) = |{v' ∈ V | v,v'∈ E}| out_grad(v) = | -""- | in_grad(v) = |{v'∈ V| (v',v) ∈ E}|
Bsp:
ungerichtet
c
|| \
|| \
b d grad(a) = | {b,b,d} | = 3
|| /
|| /
a
gerichtet
c←
| \
↓ \
b←--d out_grad(d) = 2 = | {c,b} |
| /→ in_grad(d) = 1 = | {a} |
↓ /
a
- Definition: Wege
Sei G = (v,E)
- Für v0 ∈ V ist (v0) ein Weg in G
- Für Knoten v1,...vn,vn+1 und eine Kante (vn,vn+1) ∈ E ist mit einem Weg (v0,....vn) in G auch (v0,...,vn,vn+1) ein Weg in G.
Also: Nichtleere Folgen von Knoten die durch eine Kante verbunden sind.
Eulerweg
O / \ O----O | \/ | | /\ | "Das Haus vom Nikolaus" Alle Kanten werden nur einmal passiert O----O
Hamiltonweg
O
/
O----O
/
/ Alle Knoten werden nur einmal passiert
O----O
Kreis
O / \ O O | | v0 = vn | | vi != vj Für Alle i,j i !=j; i,j >0; i,j < n O----O
Zyklen
O
/ \
O O
\ |
\ | Wie Kreis nur ohne (vi != vj)
O====O
- Definition: planare Graphen
Ist ein Graph, der auf einer Ebene gezeichnet werden kann, sodass sich die Kanten nicht schneiden!
Bsp:
1)
O
/|\
/ O \
/ / \ \
O O
2) O / \ O----O | \/ | | /\ | O----O
3) |----O @ | /@ \ | O----O | |@ / | | | / @| | O----O @ entspricht Regionen auch ausserhalb der Figur ist eine Region |@ | |-------|
1),2) und 3) sind planare Graphen.
Der K5 Graph ist kein planarer Graph da sich zwangsweise Kanten schneiden.
- Definition: dualer Graph
Der duale Graph eines geg. planaren Graphs G' ist ein Graph mit
- Knoten für jede Region
- Für jede Kante aus E gilt es gibt eine Kante, die die angrenzende Region mit Knoten verbindet.
dualer Graph
O------O
| /| \
|-|-@ / | @\---|
| | |\/ |/| O |
| | |/\ /| |/ |
| | / @ | / |
| O-+--+-O | |
| | | | |
|---|--@---|----|
- Definition: erreichbar
W ∈ V ist erreichbar von v ∈ G gdw.: es Existiert Weg(v,...w)
- Definition: Zusammenhang
G heißt zusammenhängend, wenn für Alle v,w ∈V gilt: w ist erreichbar von V
Bäume
- Definition: Baum
Ein Baum ist ein zusammenhängender, kreisfreier Graph.
Bsp.: Binary Search Tree
- Definition: erzeugender Baum
für G = (v,E) ist ein erzeigender Teilgraph mit Baumeigenschaft
Bsp.:
O O / / O O O | / / | / / O----O----O
Durchlaufen von Graphen
Tiefensuche in Graphen
Sei der Graph gegeben als Liste von Listen = g
def dfs (g,node,v=0):
if v == 0:
v = [0]*len(g) #visited-Liste
v[node] = 1 #besuche node
for t in g[node]: #gehe zu allen Nachbarn
if v[t] == 0: #falls diese noch nicht besucht
dfs(g,t,v) #Rekursion
Aufruf dfs(g,1)
=>Folge 1,2,4,3,6,7,5
Breitensuche
from Queue import *
def bfs(g,startnode)
v = [0]*len(g)
q = Queue()
v = [startnode] = 1 #besuche
q.put(startnode) #in Schlange
while not q.get()
node = q.get()
for t in q[node]
if v[t] == 0:
v[t] = 1
q.put(t)
=>Folge 1,2,3,4,5,6,7
Damenproblem
--------------- | | X | | | |---|---|---|---| | | | | X | |---|---|---|---| | X | | | | |---|---|---|---| | | | | X | ---------------
4 Damen auf einem vereinfachten Schachbrett so Positionieren, dass sich keine bedroht.
erster Durchlauf:
zweiter Durchlauf:
Weitere Anwendungen (18.06.08)
def dfs(graph):
Diese Tiefensuche tut so noch nichts weiter als zu traversieren
+ graph ist Array,
i-ter Eintrag enthaelt Adjazenzliste (auch Array) des i-ten Knotens,
wobei Knoten nummeriert von 0 ... v-i
def visit(graph, node, visited):
visited ist Array mit Flags fuer besuchte Knoten
if visited[node]: return
visited[node] = True
for neighbor in graph[node]:
visit(graph, neighbor, visited)
visited = [False]*len(graph)
for node in range(len(graph)):
visit(graph, node, visited)
Finden von Zusammenhangskomponenten
Ein moeglicher Einsatz des Verfahrens ist das Finden von Zusammenhangskomponenten (connected components).
- Beispiel: ...
- Definition: CC_i = {u_k, u_l e V: es gibt einen Pfad von u_k nach u_l ("u_l ist von u_k aus erreichbar")
- fuer ungerichtete Graphen gilt zusaetzlich: es gibt einen Pfad von u_l nach u_k}
Die Relation CC_i, also die Zusammenhangskomponenten (ZK) bilden eine Aequivalenzrelation, also kann fuer jede ZK ein Repraesentant bestimmt werden (der sog. "Anker"). Kennt jeder Knoten seinen Anker, so ist das ZK-Problem geloest.
Tiefensuchen-Algorithmus
Unser erster Ansatz ist, den Anker mit Hilfe der Tiefensuche zu finden, wobei statt Knotenbesuche Knotennummern fuer die schon gefundenen Anker gesetzt werden. Ein moeglicher Algorithmus lautet damit wie folgt:
def connectedComponents(graph):
def visit(graph, node, anchors, anchor):
anchor ist Anker der aktuellen ZK
if anchors[node] is not None: return # Anker von <node> schon bekannt
anchors[node] = anchor
for neighbor in graph[node]
visit(graph, neighbor, anchors, anchor)
anchors = [None]*len(graph)
for node in range(len(graph)):
visit(graph, node, anchors, node) # node: Anker der naechste ZK = erster Knoten der ZK
return anchors
- Beispiel: ...
Union-Find-Algorithmus
Eine Alternative (ohne Tiefensuche) waere z.B. ein Union-Find-Algorithmus. Idee dabei ist, dass eingangs jeder Knoten eine eigene ZK bildet, wobei in einer anschliessenden Rekursion Kanten gesucht werden, die zwischen den ZK bestehen.
Initialisierung: jeder Knoten wird als 1 ZK behandelt Rekursion: fasse ZK zusammen (Union) falls Kante zwischen ihnen existiert Ergebnis: Array mit dem Anker jedes Knotens
def unionFindCC(graph):
def findAnchor(anchors, k):
Prueft auf anchors[k]==k
while anchors[k] != k:
k = anchors[k]
return k
def edges(graph):
e = []
for node in range(len(graph)):
for n in graph[node]:
if node < n:
e.append((node, n))
return e
anchors = range(len(graph)) # jeder Knoten ist sein eigener Anker
for edge in edges(graph):
# diese Schleife ordnet die Anker so, dass
# der 1. Anker immer der kleinste ist
a1, a2 = findAnchor(anchors, edge[0]), findAnchor(anchors, edge[1])
if a2 < a1: a2,a1 = a1,a2
if a1 != a2: anchors[a2] = a1
for node in range(len(graph)):
# diese Schleife raeumt mit Indirektionen auf (s. Bsp. (#))
anchors[node] = findAnchor(anchors, node)
- Beispiel (#): ...
Eine verbreitete Anwendung fuer dieses Verfahren gibt es in der Bildverarbeitung:
- Beispiel: ...
Variationen der Tiefensuche (19.06.2008)
Wichtige Algorithmen, die in der Vorlesung nicht behandelt werden
- Max Flow (zur Bestimmung des maximalen Flusses durch ein Netzwerk, z.B. bei Ölpipelines)
- Matching (auch Paarung genannt): Teilmenge der Kanten eines Graphen, wobei keine zwei Kanten einen gleichen Knoten besitzen
- Anwendungsbereiche: Zuordnung von Gruppen, z.B. Arbeitsamt (Zuordnung Arbeitssuchender - Stellenangebot), Universität (Zuordnung Studenten - Übungsgruppen)
Vereinfachte Lösung für den acyclic-Algorithmus
Zum Finden von Zyklen, bzw. der Feststellung, ob ein Graph azyklisch ist, verwenden wir wieder eine modifizierte Version der Tiefensuche: Die Knoten werden wieder nach dem System der Tiefensuche besucht, und alle besuchten Knoten in einem Array visited abgespeichert. Es gibt einen Zyklus genau dann, wenn man zu einem früheren Knoten (außer zum direkten Vorgaenger) zurückkommt.
def acyclic(graph):
def visit(graph, node, fromNode, visited):
if visited[node]: # Zyklus entdeckt
return False
visited[node] = True
for neighbor in graph[node]:
if neighbor == fromNode: # überspringe Nachbar, von dem du gekommen bist
continue
if not visit(graph, neighbor, node, visited):
return False # der Graph ist zyklisch
return True # kein Zyklus
visited = [False]*len(graph)
for node in range(len(graph)):
if visited[node]: # schließt aus, dass Knoten besucht wird, der schon besucht war
continue
if not visit(graph, node, None, visited):
return False
return True
Anmerkungen zum Code:
- Wenn ein Knoten bereits besucht ist, dann gehört er zur gleichen Zusammenhangskomponente - dies hat allerdings nichts mit einem Zyklus zu tun.
- Ein Graph der einmal zyklisch war wird nie wieder azyklisch.
- Der obige Algorithmus weist Ähnlichkeiten mit den bereits behandelten Algorithmen auf: ein guter Algorithmus zeichnet sich dadurch aus, dass mit kleinen Code-Variationen ganz andere Probleme gelöst werden können.
Kürzeste Wege (Pfade)
- Definition: gewichteter Graph
Jeder Kante e ist eine reelle oder natürliche Zahl we zugeordnet (wird auch als Kantengewicht bezeichnet).
z.B.
- Abstand der Anfangs- und Endknoten
- Durchflusskapazität eines Rohres (für max-Flussprobleme)
- Wechselkurse (Darstellung in einem gerichteten Graph, da jede Kante auch eine Richtung hat. Die Knoten sind die Währungen, die Kanten sind die Wechselkurse. Auf diese Weise lassen sich unterschiedliche Wechselkurse + Bankgebühren darstellen.)
- Definition: Problem des kürzesten Weges
Sei P die Menge aller Wege von u nach v
Puv = {u_v}
und der Weg gegeben durch
u → x1 → x2 → ... → v
dann sind die Kosten eines Weges definiert durch
Kosten (Puv) = <math>\sum\limits_{l \in Pv}</math> we
- gesucht: Pfad u_v, so dass Kosten (u_v) minimal sind
- Lösung: Algorithmus von Dijkstra
Algorithmus von Dijkstra
Edsger Wybe Dijkstra
geb. 11. Mai 1930 in Rotterdam
ges. 06. August 2002
Dijkstra war ein niederländischer Informatiker und Wegbereiter der strukturierten Programmierung. 1972 erhielt er für seine Leistung in der Technik und Kunst der Programmiersprachen den Turing Award, der jährlich von der Association for Computing Machinery (ACM) an Personen verliehen wird, die sich besonders um die Entwicklung der Informatik verdient gemacht haben. Zu seinen Beiträgen zur Informatik gehören unter anderem der Dijkstra-Algorithmus zur Berechnung des kürzesten Weges in einem Graphen sowie eine Abhandlung über den go-to-Befehl und warum er nicht benutzt werden sollte. Der go-to-Befehl war in den 60er und 70er Jahren weit verbreitet, führte aber zu Spaghetti-Code. In seinem berühmten Paper "A Case against the GO TO Statement"[1], das als Brief mit dem Titel "Go-to statement considered harmful" veröffentlicht wurde, argumentiert Dijkstra, dass es umso schwieriger ist, dem Quellcode eines Programmes zu folgen, je mehr go-to-Befehle darin enthalten sind und zeigt, dass man auch ohne diesen Befehl gute Programme schreiben kann.
Algorithmus
import heapq # heapq ist ein Modul von Python
def dijkstra(graph, start, ziel): # graph: gewichtete Adjazenzliste
heap = []
visited = [None]*len(graph)
visited[start] = start
for neighbor in graph[start]:
heapq.heappush(heap, (neighbor[1], start, neighbor[0])) # neighbor[1]:Kantengewicht,neighbor[0]:Endpunkt d. K.
while len(heap) > 0: # solange der heap nicht leer ist
w, fromNode, node = heapq.heappop(heap)
if visited[node] is not None: # wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
continue
visited[node] = fromNode # baue Vorgänger-Baum
if node == ziel: # da der heap noch nicht leer ist, wird an dieser Stelle ein break benötigt
break
for neighbor in graph[node]:
if visited[neighbor[0]] is not None: # wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
continue
heapq.heappush(heap, (neighbor[1]+w, node, neighbor[0]))
bestPath = []
t = ziel
while t != visited[t]: # Array wird durchlaufen bis der Anker des Pfades gefunden ist, vgl. Union-Search
bestPath.append(t)
t=visited[t]
bestPath.append(start)
return bestPath # bestPath.reverse()
Anmerkungen zum Code:
- der graph ist eine gewichtete Adjazenzliste
| Knoten | 0 | → | Endknoten | → | Endknoten | (Nr. der Nachbarn des Knoten 0) |
| 1 | Gewicht | Gewicht | (Gewicht der jeweiligen Kante) | |||
| 2 | ||||||
| 3 |
- Eingabe z.B.:
| Knoten | 0 | → | (1, 0.3) | (3, 0.1) | (5, 1.2) | |
| 1 | → | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
- heapq() verwendet den 1. Eintrag des Tupels zum sortieren des heap
Prinzip des Dijkstra-Algorithmus
- Algorithmus ist Tiefensuche mit Prioritätswarteschlange (Heap) statt eines Stapelspeichers (Stack) → vgl. Übung 8
- Die Prioritätswarteschlange speichert die kürzesten Wege, die bereits gefunden worden sind.
- Wenn man die Prioritätswarteschlange (Heap) durch eine Warteschlange (Queue) ersetzt, erhält man Breitensuche.
- Wenn man die Prioritätswarteschlange (Heap) durch einen Stapelspeicher (Stack) ersetzt, erhält man Tiefensuche.
Beispiel
- An der Stelle "neighbor[1]" wird eine Zählvariable count eingefügt, die hoch (Breitensuche) oder runter (Tiefensuche) zählt.
- Die Gewichte werden hoch- oder runtergezählt, so wie die Kanten gesehen wurden.
- Wenn man rückwärts zählt (von 0 abziehen), werden die zuletzt hinzugefügten Kanten expandiert.
- Algorithmus von Dijkstra funktioniert nur für positive Kantengewichte
- <math>\forall</math> we > 0
- Bei negativen Kantengewichten könnte es Zyklen geben, die negative Kosten für den ganzen Zyklus haben:
/\ 1. Durchlauf: Kosten -1
1 / \ 4 2. Durchlauf: Kosten -2
/____\ etc.
2
- Verwendung bei arbitragen Geschäften (Börsengeschäfte, die die Preis-, Kurs- und Zinsunterschiede auf verschiedenen Märkten ausnutzen):
- EURO wurden in YEN, YEN in DOLLAR gewechselt und das Geld hat sich dadurch vermehrt
- Für negative Kantengewichte verwendet man den Bellman-Ford-Allgorithmus, der allerdings langsamer ist, als der Dijkstra-Algorithmus.
Komplexität von Dijkstra
- Jeder Knoten wird höchstens 1x expandiert (Iteration über die Nachbarn des Knotens).
- Jeder Knoten kann mehrmals im Heap enthalten sein.
- Es sind aber höchstens E (Anzahl der Kanten) Heap-Einträge möglich, da jede Kante höchstens 1 Heap-Eintrag generiert (ein Knoten ist nur dann im Heap, wenn man ihn über eine Kante erreicht hat, die man vorher noch nicht besucht hatte). Deshalb können nie mehr Einträge im Heap sein, als es Kanten gibt. Die Komplexität von heappush(), heappop() ist
O(log E) = O(2 log v) = O(log v)
wenn alle Kanten einen Heap-Eintrag generiert haben.
- Die while-Schleife wird im schlimmsten Fall E mal durchlaufen, deshalb ist die Komplexität von Dijkstra O(E log v).
Korrektheit von Dijkstra
- Falls
visited[node] (Schleifen-Invariante von while) != None
ist, dann liefert Zurückverfolgen des Pfades von node nach start den kürzesten Pfad von start nach node (gilt für alle Knoten, für die das visited-Feld gesetzt ist).
- Induktionsanfang: visited[start] ist einziger not-None-Fall → Bedingung erfüllt
- Induktionsschritt: wenn visited[node] gesetzt wird, ist es ein kürzester Pfad
Indirekter Beweis
Set S = {node | visited[node] != None} (alle Knoten, von denen wir den kürzesten Pfad schon kennen)
- u ist der Knoten an der Spitze des Heaps
- fromNode <math>\in</math> S (ein Nachbar von node kommt erst dann in den Heap, wenn visited[node] vorher gesetzt wurde)
- falls u → fromNode &rarr start kein kürzester Pfad wäre, müsste u's Vorgänger in V\S sein
- sei dieser Vorgänger x <math>\notin</math> S, x <math>\not=</math> u
- sei wx das Gewicht der Kante x → u, dann sind die Kosten für start nach u gleich
Kosten(start_u) = Kosten(start_x) + wx
- Annahme des indirekten Beweises:
Kosten(start_fromNode) + wfromNode
- Behauptung des indirekten Beweises:
Es gibt einen anderen Pfad x, so dass die Kosten von start nach x geringer sind
- Da aber gilt:
fromNode <math>\in</math> S und x <math>\notin</math> S
- gilt (Induktionsvoraussetzung):
Kosten(start_fromNode) < Kosten(start_x)
- Falls Kosten(start_x) < Kosten(start_u) müsste x im Heap vor u kommen; daraus folgt, dass u nicht an der Spitze des Heaps sein kann
→ Widerspruch!
→ Die Behauptung, der Weg über x ist besser, kann nicht stimmen.
→ Korrektheit von Dijkstra ist somit bewiesen.
Wie kann man Dijkstra noch verbessern?
A*-Algorithmus
- Verbesserung von Dijkstra im typischen Fall, aber die Komplexität ist immer noch =(Elog v) im schlechtesten Fall (die Komplexität kann man nicht verbessern, aber die Laufzeit im typischen Fall).
- Schätzung für jeden Knoten für den restlichen Weg:
geschätzte Gesamtkosten: Kosten(start_node) + Restschätzung(node_ziel) (exakte Kosten werden durch Dijkstra ermittelt)
Idee:
- Sortiere den Heap nach geschätzten Gesamtkosten.
- Satz:
Falls jede Schätzung den exakten Weg unterschätzt, werden die gleichen Pfade gefunden, wie bei Dijkstra (also die korrekten kürzesten Pfade).
(Die Schätzung für den restlichen Weg muss man immer so einrichten, dass der tatsächliche Weg unterschätzt wird. Da keine Straße kürzer sein kann als die Luftlinie, ist die Luftlinie eine geeignete Annahme für A*.)
- Falls der falsche Pfad im Heap eher an die Spitze kommt als der richtige Pfad, findet der A*-Algorithmus den falschen Pfad.
- Wenn der Pfad zum Ziel an der Spitze des Heap ist, dann wird keine Restschätzung mehr benötigt, denn wenn der Zielknoten aus dem Heap herrauskommt, dann hat man die exakte Berechnung. Die Restschätzung ist in diesem Fall 0. Wenn die Schätzung zu klein ist, wird der exakte Weg immer größer sein und zuerst aus dem Heap herauskommen.

Minimaler Spannbaum
(engl.: minimum spanning tree; abgekürzt: MST)
- gegeben: gewichteter Graph, zusammenhängend
- gesucht: Untermenge <math>E'\subseteq E</math>, so dass <math>\sum_{e\in E} w_e</math> minimal und G' zusammenhängend ist.
- G'definiert dann einen Baum, denn andernfalls könnte man <math>\sum_{E'}</math>verringern (eine Kante weglassen) ohne die Zusammenhangskomponente zu verletzen.
- Wenn der Graph nicht zusammenhängend ist, würde man den Spannbaum für jede Zusammenhangskomponente getrennt ausrechnen.
- Der MST ist ähnlich wie der Dijkstra-Algorithmus: Dort ist ein Pfad gesucht bei dem die Summe der Gewicht über den Pfad minimal ist.
- Beim MST suchen wir eine Lösung bei der die Summe der Gewichte über den ganzen Graphen minimal ist.
- Das Problem des MST ist nahe verwandt mit der Bestimmung der Zusammenhangskomponente, z.B. über den Tiefensuchbaum, wobei ein beliebiger Baum für die Zusammenhangskomponente und beim MST ein minimaler Baum gesucht ist.
- Anwendungen
- Wie verbindet man n Punkte mit möglichst wenigen (kurzen) Straßen (Eisenbahnen, Drähten (bei Schaltungen) usw.)?
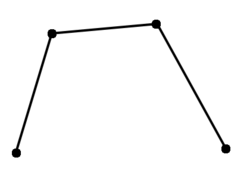

- In der Praxis: Die Festlegung, dass man nur die gegebenen Punkte verwenden darf, ist eine ziemliche starke Einschränkung.
- Wenn man sich vorstellt, es sind drei Punkte gegeben, die als gleichseitiges Dreieck angeordnet sind, dann ist der MST (siehe Abb.2, schwarz gezeichnet) und hat die Länge 2. Man kann hier die Länge als Kantengewicht verwenden.
- Wenn es erlaubt ist zusätzliche Punkte einzufügen, dann kann man in der Mitte einen neuen Punkt setzen <math>\rightarrow</math> neuer MST (siehe Abb.2, orange gezeichnet).
- Höhe = <math>\frac{1}{2}\sqrt{3}</math>, Schwerpunkt: teilt die Höhe des Dreiecks im Verhältnis 2:1; der Abstand von obersten Punkt bis zum neu eingeführten Punkt: <math>\frac{2}{3}h = \frac{\sqrt{3}}{3}</math>, davon insgesamt 3 Stück, damit (gilt für den MST in orange eingezeichnet): MST = <math>3\left(\frac{1}{3}\right) \sqrt{3} = \sqrt{3} \approx 1,7</math><br\>
- Damit ist der MST in orange kürzer als der schwarz gezeichnete MST. <br\>
<math>\Rightarrow</math>Folgerung: MST kann kürzer werden, wenn man einen Punkt dazu nimmt.
- Umgekehrt kann der MST auch kürzer werden, wenn man einen Punkt aus dem Graphen entfernt, aber wie das Beipiel des gleichseitigen Dreiecks zeigt, ist dies nicht immer der Fall.
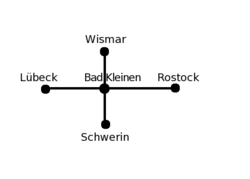
- Methode der zusätzlichen Punkteinfügung hat man früher beim Bahnstreckenbau verwendet. Durch Einführung eines Knotenpunktes kann die Streckenlänge verkürzt werden (Dreiecksungleichung).
- Bestimmung von Datenclustern
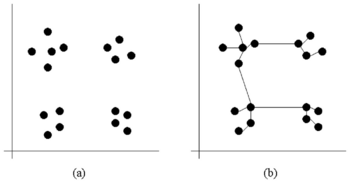
- Daten (in der Abb.: Punkte) bilden Gruppen.
- In der Abbildung hat man 2 verschiedene Messungen gemacht (als x- und y-Achse aufgetragen), bspw. Größe und Gewicht von Personen. Für jede Person i wird ein Punkt an der Koordinate (Größei, Gewichti) gezeichnet (siehe Bild a). Dies bezeichnet man als Scatter Plot. Wenn bestimmte Wertkombinationen häufiger auftreten als andere, bilden sich mitunter Gruppen aus, bspw. eine Gruppe für "klein und schwer" etc.
- Durch Verbinden der Punkte mittels eines MST (siehe Abbildung (b)) sieht man, dass es kurze (innerhalb der Gruppen) und lange Kanten (zwischen den Gruppen) gibt.
- Wenn man geschickt eine Schwelle einführt und alle Kanten löscht, die länger sind als die Schwelle, dann bekommt man als Zusammenhangskomponente die einzelnen Gruppen.
Zwei Algorithmen für dieses Problem
(im Vergleich zu Algorithmen für die Zusammenhangskomponente nur leicht verbesserte Algorithmen)
Algorithmus von Prim
- Idee: starte an der Wurzel (willkürlich gewählter Knoten) und füge jeweils die günstigste Kante hinzu (<math>\rightarrow</math> genau wie beim Dijsktra-Algorithmus, aber die Definitionen, welche Kante die günstigste ist, unterscheiden sich.)
import heapq def prim(graph): #Graphdatenstruktur ist wie bei Dijsktra heap = [] visited = [False]*len(graph) sum = 0 #wird später das Gewicht des Spannbaums sein r = [] #r ist die Lösung visited[0] = True #fixed for neighbor in graph[0]: #willkürlich 0 als Wurzel gewählt heapq.heappush(heap, (neighbor[1], 0, neighbor[0])) #Heap wird gefüllt while len(heap): wn, start, ziel = heapq.heappop(heap) if visited[ziel]: continue visited[ziel] = True #wenn visited noch nicht besetzt sum += wn #Addition des Gewichts der aktuellen Kante r.append([start, ziel]) #Kante wird an die Lsg. angehängt for neighbor in graph[ziel]: if visited[neighbor[0]]: continue heapq.heappush(heap, (neighbor[1], ziel, neighbor[0])) return sum, r
Algorithmus von Kruskal
Eine andere Vorgehensweise zur Bestimmung des minimalen Spannbaums besteht darin, einfach Kanten nacheinander hinzuzufügen und hierbei bei jedem Schritt die kürzeste Kante zu verwenden, die keinen Zyklus bildet. Anders ausgedrückt: Der Algorithmus beginnt mit N Bäumen; in N Schritten kombiniert er jeweils zwei Bäume (unter Verwendung der kürzesten möglichen Kante), bis nur noch ein Baum übrig bleibt. Der Algorithmus von J.Kruskal ist seit 1956 bekannt.
- Idee: wie beim Union-Find-Algorithmus für Zusammenhangskomponenten
- Behandle jeden Knoten als Baum für sich
- Fasse zwei Bäume zu einem neuen Baum zusammen
- für MST (im Unterschied zu Union-Find): betrachte dazu die Kanten in aufsteigender Reihenfolge der Gewichte
(priority queue; ignoriere Kanten zwischen Knoten in gleichem Baum)
- Algorithmus eignet sich besser für das Clusteringproblem, da der Schwellwert von vornerein über die Kantenlänge an den Algorithmus übergeben werden kann. Man hört mit dem Vereinigen auf, wenn die Kantenlänge den Schwellwert überschreitet.
- Es kann keine kürzere Kante als der Schwellwert mehr kommen, da die Kanten vorher sortiert worden sind.
Komplexität: gleich wie beim Dijkstra-Algorithmus, weil jede Kante kommt höchstens einmal in den Heap.
- Aufwand für Heap ist max. <math>E</math> Einträge, da jede Kante nur einmal im Heap sein kann, d.h. Heap hat den Aufwand: <math>O\left(E\log E\right)</math>, falls keine Mehrfachkanten vorhanden: <math>v^2 > E</math> und deshalb: log E < 2 log v.
- Daraus folgt, dass das dasselbe ist wie <math>O \left(E\log v\right)</math>
=> geeignet für Übungsaufgabe
Problem des Handlungsreisenden
(engl.: Traveling Salesman Problem; abgekürzt: TSP)<br\> Wikipedia (de) (en)
- Eine der wohl bekanntesten Aufgabenstellungen im Bereich der Graphentheorie ist das Problem des Handlungsreisenden.
- Hierbei soll ein Handlungsreisender nacheinander n Städte besuchen und am Ende wieder an seinem Ausgangspunkt ankommen. Dabei soll jede Stadt nur einmal besucht werden und der Weg mit den minimalen Kosten gewählt werden.
- Alternativ kann auch ein Weg ermittelt werden, dessen Kosten unter einer vorgegebenen Schranke liegen.
- gegeben: zusammenhängender, gewichteter Graph (oft vollständiger Graph)
- gesucht: kürzester Weg, der alle Knoten genau einmal (falls ein solcher Pfad vorhanden) besucht (und zum Ausgangsknoten zurückkehrt)<br\>
- auch genannt: kürzester Hamiltonpfad (Pfad der alle Knoten einmal besucht):
- - durch psychologische Experimente wurde herausgefunden, dass der Menschen (in 2D) <math>\approx</math> proportionale Zeit zur Anzahl der Knoten braucht, um den Pfad zu finden, <math>O(V)</math> (linear) (<math>\lesssim 5%</math> länger als optimaler Pfad ist typisch) <br\>
- vorgegeben: Startknoten (kann willkürlich gewählt werden), vollständiger Graph
- => v-1 Möglichkeiten für den ersten Nachfolgerknoten => je v-2 Möglichkeiten für dessen Nachfolger...
- also <math>\frac{(v-1)!}{2}</math> mögliche Wege in einem vollständigen Graphen
- Ein naiver Ansatz zur Lösung des TSP Problems ist das erschöpfende Durchsuchen des Graphen, auch "brute force" Algorithmus ("mit roher Gewalt"), indem alle möglichen Rundreisen betrachtet werden und schließlich die mit den geringsten Kosten ausgewählt wird.
- Dieses Verfahren versagt allerdings bei größeren Graphen, aufgrund der hohen Komplexität.
Systematisches Erzeugen aller Permutationen<br\>
- Allgemeines Verfahren, wie man von einer gegebenen Menge verschiedene Schlüssel - in diesem Fall: Knotennummern - sämtliche Permutationen systematisch erzeugen kann. <br\>
- Trick: erzeuge jede Permutation als Wort und betrachte dann deren lexikographische ("wie im Lexikon") Ordnung.<br\>
- Der erste unterschiedliche Buchstabe unterscheidet. Wenn die Buchstaben gleich sind, dann kommt das kürzere Wort zuerst.
gegeben: zwei Wörter a,b <br\> mathematisch formuliert, wie die Wörter im Wörterbuch sortiert sind: <br\> <math>a<b \Leftrightarrow i<min(len(a), len(b))</math><br\>
- <math>a[i] == b[i] i<j</math><br\>
- <math>a[j] < b[j] i == j</math><br\>
oder falls <math>a[i] == b[i] \forall i < n </math>
- <math>len(a) < len(b)</math>
- beginne mit dem kleinsten Wort => ist der Fall, wenn a aufsteigend sortiert
- definiere Funktion "next_permutation", die den Nachfolger in lexikographischer Ordnung erzeugt
Beispiel:
1 2 3 6 Permutationen, da !3 = 6 1 3 2 2 1 3 2 3 1 3 1 2 ----- 0 1 2 Position
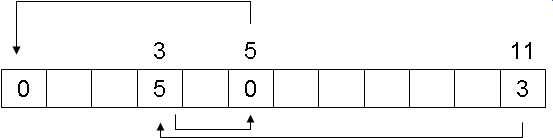
def next_permutation(a): i = len(a) -1 #letztes Element; man arbeitet sich von hinten nach vorne durch while True: # keine Endlosschleife, da i dekrementiert wird und damit irgendwann 0 wird if i <= 0: return False # a ist letzte Permutation i -= 1 if a[i]<a[i+1]: break #lexikogr. Nachfolger hat größeres a[i] j = len(a) while True: j -= 1 if a[i] < a[j]: break a[i], a[j] = a[j], a[i] #swap a[i], a[j] #sortiere aufsteigend zwischen a[i] und Ende #zur Zeit absteigend sortiert => invertieren i += 1 j = len(a) -1 while i < j: a[i], a[j] = a[j], a[i] i += 1 j-= 1 return True # eine weitere Permutation gefunden def naiveTSP(graph): start = 0 result = range(len(graph))+[start] rest = range(1,len(graph)) c = pathCost(result, graph) while next_permutation(rest): r = [start]+rest+[start] cc = pathCost(r, graph) if cc < c: c = cc result = r return c, result
Komplexität: <math>(v-1)!</math> Schleifendurchläufe (=Anzahl der Permutationen, da die Schleife abgebrochen wird, sobald es keine weiteren Permutationen mehr gibt), also
<math>O(v!) = O(v^v)</math>
- Beispiel
| i = 0 | j = 3 | |||
| ↓ | ↓ | |||
| 1 | 4 | 3 | 2 | #input für next_permutation |
| i = 2 | j = 3 | |||
| ↓ | ↓ | |||
| 2 | 4 | 3 | 1 | # vertauschen der beiden Elemente |
| i = 2 | ||||
| j = 2 | ||||
| ↓ |
| |||
| 2 | 1 | 3 | 4 | #absteigend sortiert |
- Stirling'sche Formel
Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Damit lassen sich durch die Sterling Formel z.T. starke Vereinfachungen erzielen. <math>v! \approx \sqrt{2 \pi v} \left(\frac{v}{e}\right)^v</math>
- <math>O(v!) = O\left(\sqrt{v}\left(\frac{v}{e}\right)^v\right) \approx O(v^v)</math>
Stark zusammenhängende Komponenten
geg.: gerichteter Graph
1. Bestimme die post Order Time (mit Tiefensuche) 2. Transponieren des Graphen <math>G^T</math> 3. Bestimme ConnComp <math>G^T</math> mit bekannten CC Algorithmen, aber so, dass Knoten in absteigender post Order behandelt werden
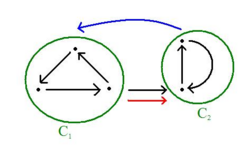
Beweis: 1.Bilde Komponentengraphen:
Knoten: jede SCC <math>C_i</math> ist ein Knoten Kanten: <math>C_i \rightarrow C_j \Leftrightarrow U_k \rightarrow U_l</math> mit <math>U_k \in C_i</math> und <math>U_l \in C_j</math>
*Eigenschaft 1: der Komponentengraph ist :azyklisch:
<math>pot \left(C_i\right) = max_{U_k \in C_i} pot\left(U_k\right)</math>
*Eigenschaft 2: falls <math>C_i \rightsquigarrow C_j</math> dann <math>pot \left(C_i\right) > pot \left(C_j\right)</math>
(ausserdem gilt: es gibt keinen Weg <math>C_j \rightsquigarrow C_i</math> )
aber: in transponierten Graphen sind alle Kanten umgedreht
*Eigenschaft 3: falls <math>{C_j}^T \rightsquigarrow {C_i}^T</math> , dann gilt <math>pot \left({C_i}^T\right) > pot \left({C_j}^T\right)</math>
Eigenschaft 2-3 <math>\Longrightarrow</math> im transponierten Graphen gibt es nie einen Pfad <math>{C_i}^T \rightsquigarrow {C_j}^T</math>
Falls <math>pot \left({C_i}^T\right) > pot \left({C_j}^T\right)</math>
<math>\Longrightarrow</math> Schritt 3 des Algorithmus kann von einem geg. Startknoten nur die Knoten derselben SCC erreichen
q.e.d.
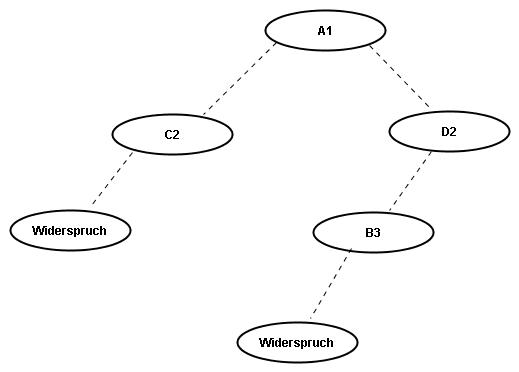
Anwendung auf 2-SAT Problem
geg.: Implikationen-Normalform, dargestellt als gerichteter Graph.
Eigenschaft: alle Variablen in derselben SCC müssen den gleichen Wert haben, weil
<math>\underbrace{x_i \rightsquigarrow x_j \stackrel{\wedge}{=} x_i \rightarrow x_j; \;\;\; x_j \rightsquigarrow x_i \stackrel{\wedge}{=} x_j \rightarrow x_i}</math>
- <math>\;\;\;x_i == x_j</math>
<math>\rightarrow \; x_i \; und \; \neg x_j</math> dürfen nie in derselben SCC sein, weil <math>\rightarrow \; x_i == \neg x_j</math> unmöglich ist
<math>\Longrightarrow</math> Algorithmus für Erfüllbarkeit: teste die Eigenschaft
Das funktioniert leider nicht für k-SAT mit <math>k>2</math>