Graphen und Graphenalgorithmen

Einführung zu Graphen

Motivation

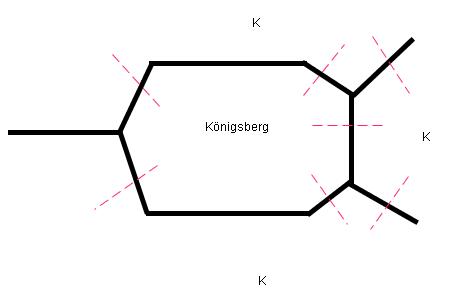
Königsberger - Brückenproblem

(1736 Euler)

Königsberger Brücken:

Spaziergang durch Königsberg, so dass alle Brücken nur einmal überquert werden.

Geometrie: Topologie

    O
   || \
   ||  \
    O   O
   ||  /
   || /
    O

• Definition: ungerichteter Graph

Ein ungerichteter Graph G = ( V, E )

• • V ist endliche Menge von Knoten (vertices)
  • E c V × V (edges)

Ein Graph heißt ungerichtet, wenn zusätzlich gilt:

(x,y) ∈ E => (y,x) ∈ E (symmetrie)

Bsp:

gerichteter Graph

ungerichtet

 O
|| \
||  \
 O   O
||  /
|| /
 O

Bsp:

• Landkarten:
  • Knoten: Länder
  • Kanten: gem. Grenzen

• Schaltkreis:
  • Knoten: Gatter
  • Kanten: Verbindungen

• Chemie (Summenformeln):
  • Knoten: Elemente
  • Kanten: Bindungen

• Soziologie (StudieVZ)
  • Soziogramm
    • Knoten: Personen
    • Kanten: Freund von ...

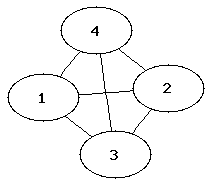
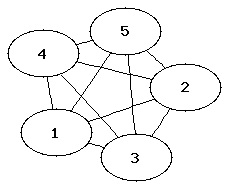
• Definition: Vollständige Graphen

Bei vollständigen Graphen ist jeder Knoten mit allen anderen Knoten verbunden.

E = U V (v,w) u (w,v) | v ∈ V, w ∈ V, u != w

k1	k2	k3
k4	k5

Rätsel Auf einer Party sind Leute. Alle stoßen miteinander an. Es hat 78 mal "Pling" gemacht. Wieviele Leute waren da?

Repräsentation von Graphen

Sei G = ( V, E ) geg und liege V in einer lineraren Sortierung vor. V = { v1, ...., vn }

Adjazenzmatrix

AG = aij = {1 falls (vi, vj) ∈ E ; sonst 0}

Bsp:

v = { a,b,c,d }     b      d
                    | \  / |
                    |  \/  |
                    |  /\  |
                    | /  \ |
                    a      c

      a b c d
     -----------
     (0 1 0 1) |a 
AG = (1 0 1 0) |b
     (0 1 0 1) |c
     (1 0 1 0) |d

Adjezenzlisten

al(v) = {v' ∈ V | (u,u') ∈ E} Lg = ((v1, al(v1)), ...., (vn, al(vn))

Python:

Array von Arrays [[...],[...],...,[...]]
                    0     1         n

• Definition: Teilgraphen

Ein Graph G' = (v',E') ist ein Teilgraph, wenn gilt:

• • v' c V
  • E' c E

Er heißt erzegender Graph, wenn zusätzlich gilt:

• • v' = V

• Definition: Knotengrade

Für G = (v,E)und v ∈ V grad(v) = |{v' ∈ V | v,v'∈ E}| out_grad(v) = | -""- | in_grad(v) = |{v'∈ V| (v',v) ∈ E}|

Bsp:

ungerichtet

 c
|| \
||  \
 b   d          grad(a) = | {b,b,d} | = 3
||  /
|| /
 a

 
gerichtet

 c←
 | \
 ↓  \
 b←--d         out_grad(d) = 2 = | {c,b} |
 |  /→          in_grad(d) = 1 = | {a} |
 ↓ /
 a

• Definition: Wege

Sei G = (v,E)

• • Für v0 ∈ V ist (v0) ein Weg in G
  • Für Knoten v1,...vn,vn+1 und eine Kante (vn,vn+1) ∈ E ist mit einem Weg (v0,....vn) in G auch (v0,...,vn,vn+1) ein Weg in G.

Also: Nichtleere Folgen von Knoten die durch eine Kante verbunden sind.

Eulerweg

   O
  /  \
 O----O
 | \/ |
 | /\ |   "Das Haus vom Nikolaus" Alle Kanten werden nur einmal passiert
 O----O

Hamiltonweg

   O
  /   
 O----O
    /  
   /      Alle Knoten werden nur einmal passiert
 O----O

Kreis

   O
  /  \
 O    O
 |    |   v0 = vn
 |    |   vi != vj   Für Alle i,j   i !=j; i,j >0; i,j < n
 O----O     

Zyklen

   O
  /  \
 O    O
   \  |
    \ |   Wie Kreis nur ohne (vi != vj)
 O====O

• Definition: planare Graphen

Ist ein Graph, der auf einer Ebene gezeichnet werden kann, sodass sich die Kanten nicht schneiden!

Bsp:

1)  

     O
    /|\
   / O \
  / / \ \
  O     O

2)

   O
  /  \
 O----O
 | \/ |
 | /\ |   
 O----O

3)

|----O   @
|   /@ \
|  O----O
|  |@ / |
|  | / @|   
|  O----O               @ entspricht Regionen auch ausserhalb der Figur ist eine Region
|@      |
|-------|

1),2) und 3) sind planare Graphen.

Der K5 Graph ist kein planarer Graph da sich zwangsweise Kanten schneiden.

• Definition: dualer Graph

Der duale Graph eines geg. planaren Graphs G' ist ein Graph mit

• • Knoten für jede Region
  • Für jede Kante aus E gilt es gibt eine Kante, die die angrenzende Region mit Knoten verbindet.

dualer Graph

     O------O
     |     /| \
   |-|-@  / | @\---|
   | | |\/  |/| O  |
   | | |/\ /| |/   |
   | | /  @ | /    |
   | O-+--+-O |    |
   |   |  |   |    |
   |---|--@---|----|

• Definition: erreichbar

W ∈ V ist erreichbar von v ∈ G gdw.:
es Existiert Weg(v,...w)

• Definition: Zusammenhang

G heißt zusammenhängend, wenn für Alle v,w ∈V gilt:
w ist erreichbar von V

Bäume

• Definition: Baum

Ein Baum ist ein zusammenhängender, kreisfreier Graph.

Bsp.: Binary Search Tree

• Definition: erzeugender Baum

für G = (v,E) ist ein erzeigender Teilgraph mit Baumeigenschaft

Bsp.:

   O    O
  /    /   
 O    O    O
 |  /    /   
 | /    /    
 O----O----O

Durchlaufen von Graphen

Tiefensuche in Graphen

Sei der Graph gegeben als Liste von Listen = g

def dfs (g,node,v=0):
  if v == 0:
    v = [0]*len(g) #visited-Liste
  v[node] = 1 #besuche node
  for t in g[node]: #gehe zu allen Nachbarn
    if v[t] == 0: #falls diese noch nicht besucht
      dfs(g,t,v) #Rekursion

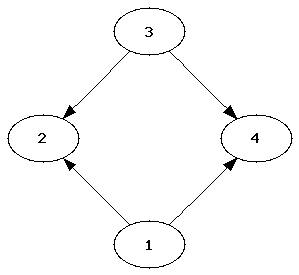
Aufruf dfs(g,1)

=>Folge 1,2,4,3,6,7,5

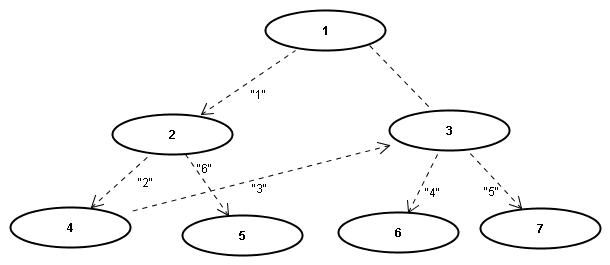
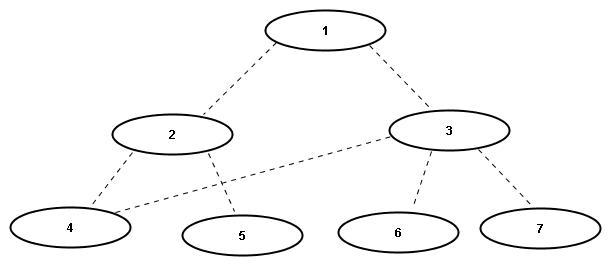
Breitensuche

from Queue import *
def bfs(g,startnode)
  v = [0]*len(g)
  q = Queue()
  v = [startnode] = 1 #besuche
  q.put(startnode) #in Schlange
  while not q.get()
    node = q.get()
    for t in q[node]
      if v[t] == 0:
        v[t] = 1
        q.put(t)

=>Folge 1,2,3,4,5,6,7

Damenproblem

 ---------------
|   | X |   |   |
|---|---|---|---| 
|   |   |   | X |
|---|---|---|---|
| X |   |   |   |
|---|---|---|---|
|   |   |   | X |
 ---------------

4 Damen auf einem vereinfachten Schachbrett so Positionieren, dass sich keine bedroht.

erster Durchlauf:

zweiter Durchlauf: