Effizienz

Bei der Diskussion von Effizienz müssen wir zwischen der Laufzeit eines Algorithmus auf einem bestimmten System und seiner prinzipiellen Leistungsfähigkeit (Algorithmenkomplexität) unterscheiden. Der Benutzer ist natürlich vor allem an der Laufzeit interessiert, denn diese bestimmt letztendlich seine Arbeitsproduktivität. Ein Softwaredesigner hingegen muss eine Implementation wählen, die auf verschiedenen Systemen und in verschiedenen Anwendungen schnell ist. Für ihn sind daher auch Aussagen zur Algorithmenkomplexität sehr wichtig, um den am besten geeigneten Algorithmus auszuwählen.

Laufzeit

Aus Anwendersicht ist ein Algorithmus effizient, wenn er die in der Spezifikation verlangten Laufzeitgrenzen einhält. Ein Algorithmus muss also nicht immer so schnell wie möglich sein, sondern so schnell wie nötig. Dies führt in verschiedenen Anwendungen zu ganz unterschiedliche Laufzeitanforderungen:

• Berechnen des nächsten Steuerkommandos für eine Maschine: ca. 1/1000s
• Berechnen des nächsten Bildes für eine Videopräsentation (z.B. Dekompression von MPEG-kodierten Bildern): ca. 1/25s

Geringere Bildraten führen zu ruckeligen Filmen.

• Sichtbare Antwort auf ein interaktives Kommando (z.B. Mausklick): ca. 1/2s

Wird diese Antwortzeit überschritten, vermuten viele Benutzer, dass der Mausklick nicht funktioniert hat, und klicken nochmals, mit eventuell fatalen Folgen. Wenn ein Algorithmus notwendigerweise länger dauert als 1/2s, sollte ein Fortschrittsbalken angezeigt werden.

• Wettervorhersage: muss spätestens am Vorabend des vorhergesagten Tages beendet sein

Laufzeitvergleich

Da die Laufzeit für den Benutzer ein so wichtiges Kriterium ist, werden häufig Laufzeitvergleiche durchgeführt. Deren Ergebnisse hängen allerdings von vielen Faktoren ab, die möglicherweise nicht kontrollierbar sind:

• Geschwindigkeit und Anzahl der Prozessoren
• Auslastung des Systems
• Größe des Hauptspeichers und Cache, Geschwindigkeit des Datenbus
• Qualität des Compilers/Optimierers (ist der Compiler für die spezielle Prozessor-Architektur optimiert?)
• Geschick des Programmierers
• Daten (Beispiel Quicksort: Best case und worst case [vorsortierter Input] stark unterschiedlich)

All diese Faktoren sind untereinander abhängig. Laufzeitvergleiche sind daher mit Vorsicht zu interpretieren. Generell sollten bei Vergleichen möglichst wenige Parameter verändert werden, z.B.

• gleiches Programm (gleiche Kompilierung), gleiche Daten, andere Prozessoren

oder

• gleiche CPU, Daten, andere Programme (Vergleich von Algorithmen)

Zur Verbesserung der Vergleichbarkeit gibt es standardisierte Benchmarks, die bestimmte Aspekte eines Systems unter möglichst realitätsnahen Bedingungen testen. Generell gilt aber: Durch Laufzeitmessung ist schwer festzustellen, ob ein Algorithmus prinzipiell besser ist als ein anderer. Dafür ist die Analyse der Algorithmenkomplexität notwendig.

Optimierung

Wenn sich herausstellt, dass ein bereits implementierter Algorithmus zu langsam läuft, geht man wie folgt vor:

1. Man verwendet einen Profiler, um zunächst den Flaschenhals zu bestimmen. Ein Profiler ist ein Hilfsprogramm, dass während der Ausführung eines Programms misst, wieviel Zeit in jeder Funktion und Unterfunktion verbraucht wird. Dadurch kann man herausfinden, welcher Teil des Algorithmus überhaupt Probleme bereitet. Donald Knuth gibt z.B. als Erfahrungswert an, dass Programme während des größten Teils ihrer Laufzeit nur 3% des Quellcodes (natürlich mehrmals wiederholt) ausführen [1]. Es ist sehr wichtig, diese 3% experimentell zu bestimmen, weil die Erfahrung zeigt, dass man beim Erraten der kritischen Programmteile oft falsch liegt. Man spricht dann von "premature optimization", also von voreiliger Optimierung ohne experimentelle Untersuchung der wirklichen Laufzeiten, was laut Knuth "the root of all evil" ist. Der Python-Profiler wird in Kapitel 25 der Python-Dokumentation beschrieben.
2. Man kann dann versuchen, die kritischen Programmteile zu optimieren.
3. Falls der Laufzeitgewinn durch Optimierung zu gering ist, muss man einen prinzipiell schnelleren Algorithmus verwenden, falls es einen gibt.

Einige wichtige Techniken der Programmoptimierung sollen hier erwähnt werden. Wenn man einen optimierenden Compiler verwendet, werden einige Optimierungen automatisch ausgeführt [2]. In Python trifft dies jedoch nicht zu. Um den Sinn einiger Optimierungen zu verstehen, benötigt man Grundkenntnisse der Computerarchitektur.

Elimination von redundantem Code

Es ist offensichtlich überflüssig, dasselbe Ergebnis mehrmals zu berechnen, wenn es auch zwischengespeichert werden könnte. Diese Optimierung wird von vielen automatischen Optimierern unterstützt und kommt im wesentlichen in zwei Ausprägungen vor:

common subexpression elimination

In mathematischen Ausdrücken wird ein Teilergebnis häufig mehrmals benötigt. Man betrachte z.B. die Lösung der quadratischen Gleichung <math>x^2+p\,x+q</math>:

       x1 = - p / 2.0 + sqrt(p*p/4.0 - q)
       x2 = - p / 2.0 - sqrt(p*p/4.0 - q)

Die mehrmalige Berechnung von Teilausdrücken wird vermieden, wenn man stattdessen schreibt:

       p2 = - p / 2.0
       r  = sqrt(p2*p2 - q)
       x1 = p2 + r
       x2 = p2 - r

loop invariant elimination

Wenn ein Teilausdruck sich in einer Schleife nicht ändert, muss man ihn nicht bei jedem Schleifendurchlauf neu berechnen, sondern kann dies einmal vor Beginn der Schleife tun. Ein typisches Beispiel hierfür ist die Adressierung von Matrizen, die als 1-dimensionales Array gespeichert sind. Angenommen, wir speichern eine NxN Matrix m in einem Array a der Größe N², so dass das Matrixelement m_ij durch a[i + j*M] indexiert wird. Wir betrachten die Aufgabe, eine Einheitsmatrix zu initialisieren. Ein nicht optimierter Algorithmus dafür lautet:

      for j in range(N):
          for i in range(N):
              if i == j:
                   a[i + j*N] = 1.0
              else:
                   a[i + j*N] = 0.0

Der Ausdruck j*N wird hier in jedem Schleifendurchlauf erneut berechnet, obwohl sich j in der inneren Schleife gar nicht verändert. Man kann deshalb optimieren zu:

      for j in range(N):
          jN = j*N
          for i in range(N):
              if i == j:
                   a[i + jN] = 1.0
              else:
                   a[i + jN] = 0.0

Vereinfachung der inneren Schleife

Generell sollte man sich bei der Optimierung auf die innere Schleife eines Algorithmus konzentrieren, weil dieser Code aum häufigsten ausgeführt wird. Insbesondere sollte man die Anzahl der Befehle in der inneren Schleife so gering wie möglich halten und teure Befehle vermeiden. Früher waren vor allem Floating-Point Befehle teuer, die man oft durch die schnellere Integer-Arithmetik ersetzt hat, falls dies algorithmisch möglich war (diesen Rat findet man noch oft in der Literatur). Heute hat sich die Hardware so verbessert, dass im Allgemeinen nur noch die Floating-Point Division deutlich langsamer ist als die anderen Operatoren. Im obigen Beispiel der quadratischen Gleichung ist es daher sinnvoll, den Ausdruck

       p2 = -p / 2.0

durch

       p2 = -0.5 * p

zu ersetzen. Dadurch spart man das Negieren von p, da der Compiler direkt mit -0.5 multipliziert, und man ersetzt eine Division durch eine Multiplikation.

Ausnutzung der Prozessor-Pipeline

Moderne Prozessoren führen mehrere Befehle parallel aus. Dies ist möglich, weil jeder Befehl in mehrere Teilschritte zerlegt werden kann. Eine generische Unterteilung in vier Teilschritte ist z.B.:

1. Dekodieren des nächsten Befehls
2. Beschaffen der Daten, die der Befehl verwendet (aus Prozessorregistern, dem Cache, oder dem Hauptspeicher)
3. Ausführen des Befehls
4. Schreiben der Ergebnisse

Man bezeichnet dies als die "instruction pipeline" des Prozessors (heutige Prozessoren verwenden wesentlich feinere Unterteilungen). Prozessoren werden nun so gebaut, dass mehrere Befehle parallel, auf verschiedenen Ausführungsstufen ausgeführt werden. Wenn Befehl 1 also beim Schreiben der Ergebnisse angelangt ist, kann Befehl 2 die Hardware zum Ausführen des Befehls benutzen, während Befehl 3 seine Daten holt, und Befehl 4 soeben dekodiert wird. Unter bestimmten Bedingungen funktioniert diese Parallelverarbeitung jedoch nicht. Dies gibt Anlass zu Optimierungen:

Vermeiden unnötiger Typkonvertierungen

Der Prozessor verarbeitet Interger- und Floating-Point-Befehle in verschiedenen Pipelines, weil die Hardwareanforderungen sehr verschieden sind. Wird jetzt ein Ergebnis von Integer nach Floating-Point umgewandelt oder umgekehrt, muss die jeweils andere Pipeline warten, bis die erste Pipeline ihre Berechnung beendet. Es kann dann besser sein, Berechnungen in Floating-Point zu Ende zu führen, auch wenn sie semantisch eigentlich Integer-Berechnungen sind.

Reduzierung der Anzahl von Verzweigungen

Wenn der Code verzweigt (z.B. durch eine if- oder while-Anweisung), ist nicht klar, welcher Befehl nach der Verzweigung ausgeführt werden soll, bevor Stufe 3 der Pipiline die Verzweigungsbedingung ausgewertet hat. Bis dahin wären die ersten beiden Stufen der Pipeline unbenutzt. Moderne Prozessoren benutzen zwar ausgefeilte Heuristiken, um das Ergebnis der Bedingung vorherzusagen, und führen den hoffentlich richtigen Zweig des Codes spekulativ aus, aber dies funktioniert nicht immer. Man sollte deshalb generell die Anzahl der Verzweigungen minimieren. Als Nebeneffekt führt dies meist auch zu besser lesbarem, verständlicherem Code. Im Matrixbeispiel kann man

      for j in range(N):
          jN = j*N
          for i in range(N):
              if i == j:
                   a[i + jN] = 1.0
              else:
                   a[i + jN] = 0.0

durch

      for j in range(N):
          jN = j*N
          for i in range(N):
              a[i + jN] = 0.0
          a[j + jN] = 1.0

ersetzen. Die Diagonalelemente a[j + jN] werden jetzt zwar zweimal initialisiert (in der Schleife auf Null, dann auf Eins), aber durch Elimination der if-Abfrage wird dies wahrscheinlich mehr als ausgeglichen, zumal dadurch die innere Schleife wesentlich vereinfacht wurde.

Ausnutzen des Prozessor-Cache

Zugriffe auf den Hauptspeicher sind sehr langsam. Deshalb werden stets ganze Speicherseiten auf einmal in den Cache des Prozessors geladen. Wenn unmittelbar nacheinander benutzte Daten auch im Speicher nahe beieinander liegen (sogenannte "locality of reference"), ist die Wahrscheinlichkeit groß, dass die als nächstes benötigten Daten bereits im Cache sind und damit schnell gelesen werden können. Bei vielen Algorithmen kann man die Implementation so umordnen, dass die locality of reference verbessert wird, was zu einer drastischen Beschleunigung führt. Im Matrix-Beispiel ist z.B. die Reihenfolge der Schleifen wichtig. Für konstanten Index j liegen die Indizes i im Speicher hintereinander. Deshalb ist es günstig, in der inneren Schleife über i zu iterieren:

      for j in range(N):
          jN = j*N
          for i in range(N):
              a[i + jN] = 0.0
          a[j + jN] = 1.0

Die umgekehrte Reihenfolge der Schleifen ist hingegen ungünstig

      for i in range(N):
          for j in range(N):
              a[i + j*N] = 0.0
          a[i + i*N] = 1.0

Jetzt werden in der inneren Schleife stets N Datenelemente übersprungen. Besonders bei großem N muss man daher häufig den Cache neu füllen, was bei der ersten Implementation nicht notwendig war. (Ausserdem verliert man hier die Optimierung jN = j*N, die jetzt nicht mehr möglich ist.)

Als Faustregel kann man durch Optimierung eine Verdoppelung der Geschwindigkeit erreichen (in Ausnahmefällen auch mehr). Benötigt man stärkere Verbesserungen, muss man wohl oder übel einen besseren Algorithmus oder einen schnelleren Computer verwenden.

Komplexität

Komplexitätsbetrachtungen ermöglichen den Vergleich der prinzipiellen Eigenschaften von Algorithmen unabhängig von einer Implementation, Umgebung etc.

Eine einfache Möglichkeit ist das Zählen der Aufrufe einer Schlüsseloperation. Beispiel Sortieren:

• Anzahl der Vergleiche
• Anzahl der Vertauschungen

Beispiel: Selection Sort

 for i in range(len(a)-1):
   max = i
   for j in range(i+1, len(a)):
     if a[j] < a[max]:
       max = j
   a[max], a[i] = a[i], a[max]      # swap

• Anzahl der Vergleiche: Ein Vergleich in jedem Durchlauf der inneren Schleife. Es ergibt sich folgende Komplexität:

  Ingesamt <math>\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1}1 = \frac{N}{2} (N-1) \!</math> Vergleiche.

• Anzahl der Vertauschungen (swaps): Eine Vertauschung pro Durchlauf der äußeren Schleife:

  Insgesamt <math>N-1 \!</math> Vertauschungen

Die Komplexität wird durch die Operationen bestimmt, die am häufigsten ausgeführt werden, hier also die Anzahl der Vergleiche. Die Anzahl der Vertauschungen ist hingegen kein geeignetes Kriterium für die Komplexität von selection sort, weil der Aufwand in der inneren Schleife ignoriert würde.

Fallunterscheidung: Worst und Average Case

Die Komplexität ist in der Regel eine Funktion der Eingabegröße (Anzahl der Eingabebits, Anzahl der Eingabeelemente). Sie kann aber auch von der Art der Daten abhängen, nicht nur von der Menge, z.B. vorsortierte Daten bei Quicksort. Um von der Art der Daten unabhängig zu werden, kann man zwei Fälle der Komplexität unterscheiden:

• Komplexität im ungünstigsten Fall

  Der ungünstigste Fall ist die Eingabe gegebener Länge, für die der Algorithmus am langsamsten ist. Der Nachteil dieser Methode besteht darin, dass dieser ungünstige Fall in der Praxis vielleicht gar nicht oder nur selten vorkommt, so dass sich der Algorithmus in Wirklichkeit besser verhält als man nach dieser Analyse erwarten würde. Beim Quicksort-Algorithmus mit zufälliger Wahl des Pivot-Elements müsste z.B. stets das kleinste oder größte Element des aktuellen Intervalls als Pivot-Element gewählt werden, was äußerst unwahrscheinlich ist.

• Komplexität im durchschnittlichen/typischen Fall

  Der typische Fall ist die mittlere Komplexität des Algorithmus über alle möglichen Eingaben. Dazu muss man die Wahrscheinlichkeit jeder möglichen Eingabe kennen, und berechnet dann die mittlere Laufzeit über dieser Wahrscheinlichkeitsverteilung. Leider ist die Wahrscheinlichkeit der Eingaben oft nicht bekannt, so dass man geeignete Annahmen treffen muss. Bei Sortieralgorithmen können z.B. alle möglichen Permutationen des Eingabearrays als gleich wahrscheinlich angenommen werden, und der typische Fall ist dann die mittlere Komplexität über alle diese Eingaben. Oft hat man jedoch in der Praxis andere Wahrscheinlichkeitsverteilungen, z.B. sind die Daten oft "fast sortiert" (nur wenige Elemente sind an der falschen Stelle). Dann verhält sich der Algorithmus ebenfalls anders als vorhergesagt.

Wir beschränken uns in dieser Vorlesung auf die Komplexität im ungünstigseten Fall. Exakte Formeln für Komplexität sind aber auch dann schwer zu gewinnen, wie das folgende Beispiel zeigt:

Beispiele aus den Übungen (Gemessene Laufzeiten für Mergesort/Selectionsort)

• Mergesort: <math>\frac{0,977N\log N}{\log 2} + 0,267N-4.39 \!</math>

  andere Lösung: <math>1140 N\log(N) - 1819N + 6413 \!</math>

• Selectionsort: <math>\frac{1}{2}N^2 - \frac{1}{2N} - 10^{-12} \!</math>

  andere Lösung: <math>1275N^2 - 116003^N + 11111144 \!</math>

Aus diesen Formeln wird nicht offensichtlich, welcher Algorithmus besser ist. Näherung: Betrachte nur sehr große Eingaben (meist sind alle Algorithmen schnell genug für kleine Eingaben). Dieses Vorgehen wird als Asymptotische Komplexität bezeichnet (N gegen unendlich).

Asymptotische Komplexität am Beispiel Polynom

Polynom: <math>a\,x^2+b\,x+c=p\!</math>

<math>x \!</math> sei die Eingabegröße, und wir betrachten die Entwicklung von <math>p \!</math> in Abhängigkeit von <math>x \!</math>.

• <math>x=0 \!</math>

  <math>p=c \!</math>

• <math>x=1 \!</math>

  <math>p=a+b+c \!</math>

• <math>x=1000 \!</math>

  <math>p=1000000a+1000b+c \approx 1000000a\!</math>

• <math>x \to \infty \!</math>

  <math>p \approx x^2a\!</math>

Für sehr große Eingaben verlieren also b und c immer mehr an Bedeutung, so dass am Ende nur noch a für die Komplexitätsbetrachtung wichtig ist.

O-Notation

• Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme.
• Formale Definition:

  Asymptotische Komplexität

  Für zwei Funktionen f(x) und g(x) definiert man

  <math>f(x) \in \mathcal{O}(g(x))</math>

  (sprich "f ist in O von g" oder "f ist von derselben Größenordnung wie g") genau dann wenn es eine Konstante <math>c>0</math> und ein Argument <math>x_0</math> gibt, so dass

  <math>\forall x \ge x_0:\quad f(x) \le c\,g(x)</math>.

  Die Menge <math>\mathcal{O}(g(x))</math> aller durch g(x) abschätzbaren Funktionen ist also formal definiert durch

  <math>\mathcal{O}(g(x)) = \{ f(x)\ |\ \exists c>0: \forall x_0 \ge x: f(x) \le c\,g(x)\}</math>

Die Idee hinter dieser Definition ist, dass g(x) eine wesentlich einfachere Funktion ist als f(x), die sich aber nach geeigneter Skalierung (Multiplikation mit c) und für große Argumente x im wesentlichen genauso wie f(x) verhält. Man kann deshalb in der Algorithmenanalyse f(x) durch g(x) ersetzen. <math>f(x) \in \mathcal{O}(g(x))</math> spielt für Funktionen eine ähnliche Rolle wie der Operator ≤ für Zahlen: Falls a ≤ b gilt, kann bei einer Abschätzung von oben ebenfalls a durch b ersetzt werden.

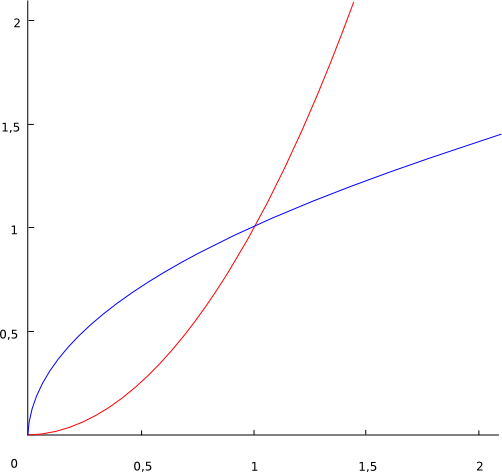
Ein einfaches Beispiel

Rot = <math>x^2 \!</math> Blau = <math>\sqrt{x} \!</math>

<math>\sqrt{x} \in \mathcal{O}(x^2)\!</math> weil <math>\sqrt{x} \le c\,x^2\!</math> für alle <math>x \ge x_0 = 1 \!</math> und <math>c = 1\!</math>, oder auch für <math>x \ge x_0 = 4 \!</math> und <math>c = 1/16</math> (die Wahl von c und x₀ in der Definition von O(.) ist beliebig, solange die Bedingungen erfüllt sind).

Komplexität bei kleinen Eingaben

Algorithmus 1: <math>\mathcal{O}(N^2) \!</math>
Algorithmus 2: <math>\mathcal{O}(N\log{N}) \!</math>

Algorithmus 2 ist schneller (von geringerer Komplexität) für große Eingaben, aber bei kleinen Eingaben (insbesondere, wenn der Algorithmus in einer Schleife immer wieder mit kleinen Eingaben aufgerufen wird) könnte Algorithmus 1 schneller sein, falls der in der <math>\mathcal{O}</math>-Notation verborgene konstante Faktor c bei Algorithmus 2 einen wesentlich größeren Wert hat als bei Algorithmus 1.

Eigenschaften der O-Notation (Rechenregeln)

1. Transitiv:

   <math>f(x) \in \mathcal{O}(g(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) \in \mathcal{O}(h(x)) \!</math>

2. Additiv:

   <math>f(x) \in \mathcal{O}(h(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) + g(x) \in \mathcal{O}(h(x)) \!</math>

3. Für Monome gilt:

   <math>x^k \in \mathcal{O}(x^k)) \land x^k \in \mathcal{O}(x^{k+j}), \forall j \ge 0 \!</math>

4. Multiplikation mit einer Konstanten:

   <math>f(x) \in \mathcal{O}(g(x)) \to c\,f(x) \in \mathcal{O}(g(x))\!</math>

   andere Schreibweise:

   <math>f(x) = c\,g(x) \to f(x) \in \mathcal{O}(g(x))\!</math>

5. Folgerung aus 3. und 4. für Polynome:

   <math>a_0+a_1\,x + ... + a_n\,x^n \in \mathcal{O}(x^n)\!</math>

   Beispiel: <math>a\,x^2+b\,x+c \in \mathcal{O}(x^2)\!</math>

6. Logarithmus:

   <math>a, b \neq 1\!</math>

   <math>\log_{a}{x} \in \mathcal{O}(\log_{b}{x})\!</math>

   Die Basis des Logarithmus spielt also keine Rolle.

   Beweis hierfür:

   <math>\log_{a}{x} = \frac{\log_{b}{x}}{\log_{b}{a}}\!</math>

   Mit <math>c = 1 / \log_{b}{a}\,</math> gilt: <math>\log_{a}{x} = c\,\log_{b}{x}\!</math>.

   Wird hier die (zweite) Regel für Multiplikation mit einer Konstanten angewendet, fällt der konstante Faktor weg, also <math>\log_{a}{x} \in \mathcal{O}(\log_{b}{x})\!</math>.

   Insbesondere gilt auch <math>\log_{a}{x} \in \mathcal{O}(\log_{2}{x})\!</math>, es kann also immer der 2er Logarithmus verwendet werden.

O-Kalkül

Das O-Kalkül definiert wichtige Vereinfachungsregeln for Ausdrücke in O-Notation:

1. <math>f(x) \in \mathcal{O}(f(x))\!</math>
2. <math>\mathcal{O}(\mathcal{O}(f(x))) \in \mathcal{O}(f(x))\!</math>
3. <math>c\,\mathcal{O}(f(x)) \in \mathcal{O}(f(x))\,</math> für jede Konstante c
4. <math>\mathcal{O}(f(x))+c \in \mathcal{O}(f(x))\,</math> für jede Konstante c
5. Sequenzregel:

   Wenn zwei nacheinander ausgeführte Programmteile die Komplexität <math>\mathcal{O}(f(x))</math> bzw. <math>\mathcal{O}(g(x))</math> haben, gilt für beide gemeinsam:

   <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(f(x))</math> falls <math>g(x) \in \mathcal{O}(f(x))</math> bzw.

   <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(g(x))\!</math> falls <math>f(x) \in \mathcal{O}(g(x))</math>.

   Informell schreibt man auch: <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(max(f(x), g(x)))\!</math>

6. Schachtelungsregel bzw. Aufrufregel:

   Wenn in einer geschachtelten Schleife die äußere Schleife die Komplexität <math>\mathcal{O}(f(x))</math> hat, und die innere <math>\mathcal{O}(g(x))</math>, gilt für beide gemeinsam:

   <math>\mathcal{O}(f(x)) * \mathcal{O}(g(x)) \in \mathcal{O}(f(x) * g(x))\!</math>.

   Gleiches gilt wenn eine Funktion <math>\mathcal{O}(f(x))</math>-mal aufgerufen wird, und die Komplexität der Funktion selbst <math>\mathcal{O}(g(x))</math> ist.

O-Kalkül auf das Beispiel des Selectionsort angewandt

Selectionsort: Wir hatten gezeigt dass <math>f(N) = \frac{N^2}{2} - \frac{N}{2}</math>. Nach der Regel für Polynome vereinfacht sich dies zu <math>f(N) \in \mathcal{O}\left(\frac{N^2}{2}\right) \in \mathcal{O}(N^2)\!</math>.

Alternativ via Schachtelungsregel:

Die äußere Schleife wird (N-1)-mal durchlaufen: <math>N-1 \in \mathcal{O}(N)</math>

Die innere Schleife wird (N-i-1)-mal durchlaufen. Das sind im Mittel N/2 Durchläufe: <math>N/2 \in \mathcal{O}(N)</math>

Zusammen: <math>\mathcal{O}(N)*\mathcal{O}(N) \in \mathcal{O}(N^2)</math>

Nach beiden Vorgehensweisen kommen wir zur Schlussfolgerung, dass der Selectionsort die asymptotische Komplexität <math>\mathcal{O}(N^2)\!</math> besitzt.

Zusammenhang zwischen Komplexität und Laufzeit

Wenn eine Operation 1ms dauert, erreichen Algorithmen verschiedener Komplexität folgende Leistungen (wobei angenommen wird, dass der in der <math>\mathcal{O}</math>-Notation verborgene konstante Faktor immer etwa gleich 1 ist):

Komplexität	Operationen in 1s	Operationen in 1min	Operationen in 1h
<math>\mathcal{O}(N)</math>	1000	60.000	3.600.000
<math>\mathcal{O}(N\log_2{N})</math>	140	4895	204094
<math>\mathcal{O}(N^2)</math>	32	245	1898
<math>\mathcal{O}(N^3)</math>	10	39	153
<math>\mathcal{O}(2^N)</math>	10	16	21

Exponentielle Komplexität

Der letzte Fall <math>\mathcal{O}(2^N)</math> ist von exponentieller Komplexität. Das bedeutet, dass eine Verdopplung des Aufwands nur bewirkt, dass die maximale Problemgröße um eine Konstante wächst. Algorithmen mit exponentieller (oder noch höherer) Komplexität werden deshalb als ineffizient bezeichnet. Algorithmen mit höchstens polynomieller Komplexität gelten hingegen als effizient.

In der Praxis sind allerdings auch polynomielle Algorithmen mit hohem Exponenten meist zu langsam. Als Faustregel kann man eine praktische Grenze von <math>\mathcal{O}(N^3)</math> ansehen. Bei einer Komplexität von <math>\mathcal{O}(N^3)</math> bewirkt ein verdoppelter Aufwand immer noch eine Steigerung der maximalen Problemgröße um den Faktor <math>\sqrt[3]{2}</math> (also eine multiplikative Vergrößerung um ca. 25%, statt nur einer additiven Vergrößerung wie bei exponentieller Komplexität).

(Vorlesung 8.5.)

Beispiel: Gleitender Mittelwert (Running Average)

Wir berechnen für ein gegebenes Array a einen gleitenden Mittelwert über k Elemente:

<math>r_i = \frac{1}{k} \sum_{j=i-k+1}^i a_j</math>

Das heisst, für jedes i mitteln wir die letzten k Elemente von a und schreiben das Ergebnis in r[i]. Diese Operation ist z.B. bei Börsenkursen wichtig: Neben dem aktuellen Kurs für jeden Tag wird dort meist auch der gleitende Mittelwert der letzten 30 Tage sowie der letzten 200 Tage angegeben. In diesen Mittelwerten erkennt man besser die langfristige Tendenz, weil die täglichen Schwankungen herausgemittelt werden. Wir nehmen außerdem an, dass

• Array-Zugriff hat eine Komplexität von O(1)
• <math>k \ll N</math>, d.h. <math>N-k\approx N</math>.

Die beiden folgenden Algorithmen berechnen die Mittelwerte auf unterschiedliche Art. Der linke folgt der obigen Definition durch eine Summe, während der rechte inkrementell arbeitet: Man kann den Bereich der k letzten Werte als Fenster betrachten, das über das Array a geschoben wird. Schiebt man das Fenster ein Element weiter, fällt links ein Element heraus, und rechts kommt eins hinzu. Man muss also nicht jedes Mal die Summe neu berechnen, sondern kann den vorigen Wert aktualisieren. Wir werden sehen, dass dies Folgen für die Komplexität des Algorithmus hat.

Schritte	Version 1: O(N * k)	Komplexität	Version 2: O(N)	Komplexität
1.	r = [0] * len(a)	O(N)	r = [0] * len(a)	O(N)
2.	if k > len(a):	O(1)	if k > len(a):	O(1)
3.	raise RuntimeError ("k zu groß")		raise RuntimeError ("k zu groß")
4.	for j in range(k, len(a)):	O(N-k) = O(N)	for i in range(k):	O(k)
5.	for i in range(j-k+1, j+1):	O(k)	r[k] += a[i]	O(1)
6.	r[j] += a[i]	O(1)	for j in range(k+1, len(a)):	O(N-k) = O(N)
7.	r[j] /= float(k)	O(1)	r[j] = (a[j] - a[j-k] + r[j-1])	O(1)
8.	return r	O(1)	for j in range(len(a)):	O(N)
9.			r[j] /= float(k)	O(1)
10.			return r	O(1)

Obwohl Version 2 mehr Zeilen benötigt, besitzt das Programm eine geringere Komplexität.

Berechnung der Komplexität

Berechnung der Komplexität von Version 1

(Wiederholung der Rechenregeln:siehe Vorlesung 7.5.)

Zuweisungen
äußere Schleife = f(x)
innere Schleife = g(x)

4. Schritt: for j in range(k, len(a)) = äußere Schleife

f(x) = O(N)(siehe Tabelle)

5. Schritt: for i in range(j-k+1, j+1) = innere Schleife

g(x) = O(k)

Multiplikationsregel (für geschachtelte Schleifen):
O(f(x)) * O(g(x)) ∈ O(f(x) * g(x))

Multiplikationsregel angewendet auf Version 1
O(N) * O(k) ∈ O(N * k)
Komplexität von Version 1 = O(N * k)

Berechnung der Komplexität von Version2

siehe Tabelle

Zuweisungen

6.Schritt: for j in ange(k+1, len(a)):

f₁(x) = O(N)

8.Schritt: for j in range(len(a)):

f₂(x) = O(N)

4.Schritt: for i in range(k):

g(x) = O(k)

Additionsregel (für nacheinander ausgeführte Programmteile):
O(f(x) + g(x)) = O(f(x)) falls g(x) ∈ O(f(x))
O(f(x) + g(x)) ∈ O(g(x)) falls f(x) ∈ O(g(x))
oder kurz O(f(x) + g(x)) = O(max(f(x),g(x)))

Anwendung der Additionsregel auf Version 2
O(f₁(x)) + O(f₂(x)) + O(g(x))
O(N) + O(N) +O(k) = O(N), weil O(k) ∈ O(N) [O(max(O(N),O(k)))]
(da wir wissen O(k) < O(N):
if k > len(a):

raise RuntimeError("k zu groß")

Daraus folgt:
→ k < len(a) → for-Schleifen die über k iterieren haben eine kleinere Komplexität als for-Schleifen die über len(a) iterieren)

Komplexität von Version 2 = O(N)

Fazit

Obwohl Version 2 mehr Schritte benötigt hat sie eine geringere Komplexität, da die for-Schleifen nicht wie bei Version 1 verschachtelt/untergeordnet sind. Bei verschachtelten for-Schleifen muss die Multiplikationsregel angewendet → höhere Komplexität

Die gerade berechnete Komplexität gilt nur unter der Annahme, dass Array-Zugriffe eine Komplexität von O(1) besitzen

Allgemein: Algorithmen-Analysen beruhen auf der Annahme, dass Zugriff auf die Daten optimal schnell sind, dass heißt dass die geeigneteste Datenstruktur verwendetet wird. → Ansonsten: Komplexitätsverschlechterung!

Beispiel für eine Verschlechterung der Komplexität durch Verwendung einer nicht optimalen Datenstruktur

Beispiel: Verwende eine verkettete Liste anstalle eines Arrays. Um auf das j-te Element der Liste zuzugreifen, muss die Liste bis dahin durchlaufen werden

Implementation von L[j] für verkettete Liste	Komplexität
r = L.head	O(1)
while j > 0:	O(j)
r = r.next	O(1)
j -= 1	O(1)
return r.data	O(1)

<math> \Bigg\rbrace </math> O(j)
r[j] = r[j] + a[i] → O(1) → O(N), falls a[i]= O[N]

Fazit:

Wegen der Schleife hat der Array-artige Zugriff bei einer verketteten Liste eine Komplexität von O(N).
Würden wir in unserem running Average-Beispiel(siehe oben) auf eine verkettete Liste zugreifen hätten wir anstatt O(1) eine Komplexität von O(N) für den Zugriff auf unser Array.

Beispiel: Running-Average mit verketteter Liste

Schritte	Version 1 mit verketteter Liste: O(N2 * k)	Komplexität
1.		O(N)
2.	if k > len(a):	O(1)
3.	raise RuntimeError ("k zu groß")
4.	for j in range(k, len(a)):	O(N-k) = O(N)
5.	for i in range(j-k+1, j+1):	O(k)
6.	r[j] += a[i]	O(i) = O(N)
7.	r[j] /= float(k)	O(1)
8.	return r	O(1)

Die Änderung gegenüber der ursprünglichen Version ist in Zeile 6. Der Zugriff a[i] erfolgt jetzt auf eine Liste, nicht auf ein Array. Aufgrund der obigen Implementation dieses Zugriffs verbirgt sich dahinter eine weitere Schleife. Das heisst, wir haben jetzt drei geschachtelte Schleifen. Zuweisungen
äußere Schleife = f₂(x)
innere Schleife = g(x)

verkettete Liste

f₁(x) = O(N)

4. Schritt: for j in range(k, len(a)) = äußere Schleife

f₂(x) = O(N)(siehe Tabelle)

5. Schritt: for i in range(j-k+1, j+1) = innere Schleife

g(x) = O(k)

Multiplikationsregel ohne Konstante:
O(f(x) * O(g(x)) ∈ O(f(x) * g(x))

Multiplikationsregel angewendet auf Version 1 mit einer verketteten Liste

O(N) * O(N) * O(k) ∈ O(N² * k)

Die Komplexität von Version 1 mit einer verketteten Liste wäre O(N² * k)

→ Die richtige Datenstruktur ist wichtig, da es sonst zu einer Komplexitätsverschlechterung kommen kann!

Auf Version 2 unseres runningAverage-Beispiels hätte eine verkettete Liste allerdings keine Auswirkungen, da die Additionsregel bei der Komplexitätsberechnung angewendet würde und somit Version 2 immer noch eine Komplexität von O(N) hätte.

Amortisierte Komplexität

Bis jetzt wurde die Komplexität nur im schlechtesten Fall(Worst Case) betrachtet, die Komplexität im schlechtesten Fall schwankt jedoch.
Die amortisierte Komplexität beschäftigt sich mit der Komplexität im durschnittlichen/typischen Fall(Average Case)

Zum weiter Lesen: [Wikipedia: Amortisierte Laufzeitanalyse]

Beispiel: Inkrementieren von Binärzahlen

Frage: Was kostet eine Operation im Durchschnitt?

Annahme: Bei jeder Operation wird ein Gehalt vom Wert 1 bezahlt, dass dem Guthaben zugeschrieben wird, wenn die Kosten das Gehalt decken.

Kosten <= Gehalt → es wird gespart

Kosten > Gehalt → Guthaben - Gehalt werden für die Kosten verbraucht

Schritte	Zahlen	Kosten	Kosten + Sparen	Guthaben
1.	00001	1	2	1
2.	00010	2	2	1
3.	00011	1	2	2
4.	00100	3	2	1

Die Kosten ergeben sich aus der Anzahl der Ziffern die von 1 nach 0, bzw. von 0 nach 1 verändert werden

Rechnung:

1. Schritt: Kosten: 1 <= Gehalt: 1

→ es wird gespart

2. Schritt: Kosten: 2 > Gehalt: 1

→ es wird nicht gespart

→ Guthaben bleibt so wie es ist

3. Schritt: Kosten: 1 <= Gehalt: 1

→ es wird gespart

4. Schritt: Kosten: 3 > Gehalt: 1

→ Guthaben: 2 - Gehalt: 1 = 1

→ es wird eine 1 vom Guthaben genommen um die Kosten zu zahlen

Zum weiter Lesen: [Wikipedia Account-Methode]

Fazit

Die amortisierte Komplexität beschäftigt sich mit dem Durchschnitt aller Operation im ungünstigsten Fall. Operationen mit hohen Kosten, die aber nur selten ausgeführt werden, fallen bei der amortisierten Komplexität nicht so ins Gewicht. Bei Algorithmen, die gelegentlich eine "teure" Operation benutzen, ansonsten jedoch "billigen" Operationen aufrufen, kann die amortisierte Komplexität niedriger sein also die Komplexität im schlechtesten (Einzel-)Fall.

In unserem Beispiel fällt der 4. Schritt bei den Kosten schlußendlich nicht so ins Gewicht, da wir die Kosten aus unserem Guthaben mitbezahlen können → tatsächliche Kosten = 3, Kosten + Sparen = 2

→ Der Algorithmus besitzt durch dieses Verfahren eine niedrigere Komplexität

statisches Array

Ein statisches Array hat eine feste Größe N und besitzt eine Komplexität von O(N).
Wird das Array um ein Element erweitert, muss ein neues Array mit der Größe N+1 erzeugt werden.

Anhängen eines weiteren Elements an ein statisches Array:

Schritte	Array (wie es aussehen könnte)	Komplexität
altes Array	[0,1,2,3]	-
1. Array N+1	[None,None,None,None,None]	O(N+1) = O(N)
2. Kopieren	[0,1,2,3,None]	O(N)
3. append von "x"	[0,1,2,3,'x']	O(1)

altesArray = [0,1,2,3]
altesArray.append('x')

1. Es wird ein neues Array der Größe N+1 erzeugt
2. Die Daten aus dem alten Array werden in das neue Array mit der Länge N+1 kopiert
(Die Operation besitzt nur eine Komplexität von O(N), wenn das Kopieren eines Elements eine Komplexität von O(1) besitzt)
3. 'x' wird an die letzte Stelle des neuen Arrays geschrieben

Additionsregel:
O(N) + O(N) + O(1) ∈ O(N), falls O(1) ∈ O(N) [O(max(O(N),O(1))] (Bedingung: N > 1)

dynamisches Array

Beim dynamischen Array werden mehr Speicherelemente reserviert als zur Zeit benötigt. Es gibt verschiedene Möglichkeiten wie ein dynamisches Array realisiert werden kann.

capacity = Anzahl der möglichen Elemente, die in das Array passen
size = Anzahl der Elemente, die im Array gespeichert sind
data = statisches Array der Größe "capacity"
A

Beispiele für mögliche Vorgehensweisen eines dynamischen Arrays beim Zufügen eines neuen Elements: (size == capacity)

• Ein neues statisches Array der Größe size == capacity wird erzeugt
• capacity wird verdoppelt
  

→ neue capacity = 2 * alte capacity

• capacity wird um einen Prozentsatz vergrößert
  

→ neue capacity = alte capacity * c, c > 1

• ...

Folge: Das Hinzufügen eines neuen Elements in ein dynamisches Array ist amortisiert, die Operation besitzt eine Komplexität von O(1).

Analyse des dynamischen Arrays

Durchschnitt der Gesamtkosten für N-maliges append = <math>\frac{1}{N} \sum_{i = 1}^N Kosten(i)</math>

Fall 1: Array ist nicht voll
Es wird kein Umkopieren benötigt, da das Array noch nicht voll ist → size < capacity

Kosten: 1
Potenzial vor append: Φ_i-1 = 2(i - 1) - capacity
Potenzial nach append: Φ_i - capacity

amortisierte Kosten = Kosten_i + Φ_(i) - Φ_(i-1)

= 1 + (2i - capacity) - [2(i - 1) - capacity]

= 1 + 2i - capacity - 2i + 2 + capacity

= 1 + 2i - capacity - 2i + 2 + capacity

= 1 + 2

= 3 = O(1) → konstant

Fall 2: Array ist voll
Umkopieren wird nach i-tem append benötigt → size == capacity

Kosten: (i-1) + 1
Potenzial vor append = Φ_i-1 = 2(i - 1) - capacity
Potenzial nach append = Φ_i = 2i - 2 * capacity

= 2i - 2i , da capacity = i

= 0

amortisierte Kosten = Kosten_i + Φ_(i) - Φ_(i-1)

= ((i - 1) + 1) + 0 - [2(i-1) - capacity]

= i - 2i - 2 - capacity

= i - 2i - 2 - capacity

= i - 2 - capacity , da capacity = i

= 2 = O(1) → konstant

Damit wurde bewiesen, dass die Operation append beim dynamischen Array amortisiert ist → O(1)

Landau-Symbole

Um die asymptotische Komplexität verschiedener Algorithmen miteinander vergleichen zu können, verwendet man die sogenannten Landau-Symbole. Das wichtigste Landau-Symbol ist <math>\mathcal{O}</math>, mit dem man eine obere Schranke für die Komplexität angeben kann.

Schreibt man <math>f \in \Omega(g)</math>, so stellt dies eine asymptotische untere Schranke für die Funktion f dar.

Schließlich bedeutet <math>f \in \Theta(g)</math>, dass die Funktion f genauso schnell wie die Funktion g wächst, das heißt man hat eine asymptotisch scharfe Schranke für f. Hierzu muss sowohl <math>f\in\mathcal{O}(g)</math> als auch <math>g\in\mathcal{O}(f)</math> erfüllt sein.

Im nun folgenden soll auf die verschiedenen Landau-Symbole noch näher eingegeangen werden.

<math>\mathcal{O}</math> - Notation

<math>f \in \mathcal{O}(g)</math> ist eine Abschätzung der asymptotischen Komplexität der Funktion f von oben. Per Definition gilt <math>f(N) \in \mathcal{O}(g(N))</math> genau dann, falls eine Konstante

<math> c > 0 </math> existiert, so dass

<math> f(N) \le c \cdot g(N) </math> für <math> N \ge N_0 </math>

erfüllt ist.

Im Prinzip ist <math>f \in \mathcal{O}(g)</math> also ein <-Operator für Funktionen, analog zum <-Operator für Zahlen.

<math>\Omega</math>- Notation

<math>f \in \Omega(g) </math> schätzt die asymptotische Komplexität der Funktion f nach unten ab.

Formal kann man <math>f(N) \in \Omega(g(N)) </math> genau dann schreiben, falls es eine Konstante <math> c > 0 </math> gibt, so dass

<math> f(N) \ge c \cdot g(N) </math> für <math> N \ge N_0 </math>

gilt. Man verwendet diese Notation also um abzuschätzen, wie groß der Aufwand (die Komplexität) für einen bestimmten Algorithmus mindestens ist und nicht höchstens, was man mit der <math>\mathcal{O}</math> - Notation ausdrücken würde.

Ein praktisches Beispiel für eine Anwendung der <math>\Omega</math>- Notation wäre die Fragestellung, ob es prinzipiell einen besseren Algorithmus für ein bestimmtes Problem gibt. Wie später in der Vorlesung gezeigt werden wird, ist das Sortieren eines Arrays beispielsweise immer mindestens von der Komplexität <math> \Omega(N\cdot \ln N) </math>, was konkret bedeutet, dass kein Sortieralgorithmus jemals eine geringere Komplexität als Merge-Sort beispielsweise haben wird. Natürlich kann man den entsprechenden Sortieralgorithmus, also Merge-Sort zum Beispiel, unter Umständen noch optimieren, aber die Komplexität wird erhalten bleiben. Mit diesem Wissen kann man sich viel (vergebene) Arbeit sparen.

<math>\Theta</math>- Notation

<math>f(N) \in \Theta(g(N))</math> ist eine scharfe Abschätzung der asymptotischen Komplexität einer Funktion f.

Damit dies gilt, muss <math>f(N) \in \mathcal{O}(g(N))</math> und gleichzeitig <math>f(N) \in \Omega(g(N))</math> erfüllt sein.

Dies ist natürlich auch die beste Abschätzung der asymptotischen Komplexität einer Funktion f. Formal bedeutet <math>f(N) \in \Theta(g(N))</math> dass es zwei Konstanten <math> c_1 </math> und <math> c_2 </math>, beide größer als Null, gibt, so dass für alle <math> N \geq N_0 </math> gilt:

<math> c_1 \cdot g(N) \leq f(N) \leq c_2 \cdot g(N) </math>.

In der Praxis verwendet man jedoch statt der <math>\Theta</math>- Notation oft die <math>\mathcal{O}</math> - Notation.

Komplexitätsvergleich zweier Algorithmen

In diesem Abschnitt wollen wir der Frage nachgehen, wie ein formaler Beweis für die Behauptung <math> f(N) \in \mathcal{O}(g(N))</math> geschehen kann. Hierbei werden zwei Beweismethoden vorgestellt werden, und zwar der Beweis über die Definition der Komplexität sowie der Beweis durch Dividieren.

Beweis über die Definition der asymptotischen Komplexität

Die Definition der asymptotischen Komplexität <math>f(N) \in \mathcal{O}(g(N))</math> war:

Es gibt eine Konstante <math> c > 0 </math>, so dass <math> f(N) \le c \cdot g(N) </math> für <math> N \ge N_0 </math> erfüllt ist.

Um also die die asymptotische Komplexität <math>f(N) \in \mathcal{O}(g(N))</math> zu beweisen, muss man die oben erwähnten Konstanten c und <math> N_0 </math> finden, so dass

<math> f(N) \leq g(N) </math> für alle <math> N \ge N_0 </math> erfüllt ist.

Dies geschieht zweckmäßigerweise mit dem Beweisprinzip der vollständigen Induktion. Hierbei ist zu zeigen, dass

1. <math> f(N_0) \leq g(N_0) </math> für die eine zu bestimmende Konstante <math> N_0 </math> gilt (Induktionsanfang) und
2. falls <math> f(N) \leq g(N) </math>, dann auch <math> f(N+1) \leq g(N+1) </math> (Induktionsschritt) gilt.

Beweis durch Dividieren

Hierbei wählt man eine Konstante c und zeigt, dass <math> \lim_{N \rightarrow \infty} \frac{f(N)}{c \cdot g(N)} \leq 1 </math> gilt.

Als Beispiel betrachten wir die beiden Funktionen <math> f(N) = N \lg N </math> und <math> g(N) = N^2 </math> und wollen zeigen, dass <math>f(N) \in \mathcal{O}(g(N))</math> gilt. Als Konstante c wählen wir <math> c = 1 </math>.

<math> \lim_{N \rightarrow \infty} \frac{f(N)}{g(N)} = \lim_{N \rightarrow \infty} \frac{\lg N}{N} = \frac{\infty}{\infty} </math>

Unbestimmte Ausdrücke der Form <math> \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} </math>, in denen sowohl <math> f(x) </math> als auch <math> g(x) </math> mit <math> x \rightarrow x_0 </math> gegen Null oder gegen Unendlich streben, kann man manchmal mit den Regeln von l'Hospital berechnen. Danach darf man die Funktionen f und g zur Berechnung des unbestimmten Ausdrucks durch ihre k-ten Ableitungen ersetzen:

<math> \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = \lim_{x \rightarrow x_0} \frac{f^{(k)}(x)}{g^{(k)}(x)} </math>

In unserem Fall verwenden wir die erste Ableitung und erhalten: <math> \lim_{N \rightarrow \infty} \frac{f'(x)}{g'(x)} = \lim_{N \rightarrow \infty} \frac{1/N}{1} \rightarrow 0 </math>

Damit wurde <math>f(N) \in \mathcal{O}(g(N))</math>, also <math>N \lg N \in \mathcal{O}(N^2)</math> gezeigt. Man beachte hierbei, dass <math>N \lg N \in \mathcal{O}(N^2)</math> keine enge Grenze für die Komplexität von <math>N \lg N)</math> darstellt, da der Grenzwert <math> \lim_{N \rightarrow \infty} \frac{f'(x)}{g'(x)} </math> gegen 0 und nicht gegen eine von Null verschiedene Konstante strebt. In diesem Fall haben wir also die Komplexität von <math>N \cdot \lg N </math> nur nach oben abschätzen können.

Array (wie es aussehen könnte)	size	capacity	Kosten 1.append	Summe Kosten	Durchschnittskosten	Φi = 2 * size - capacity (i = size)	Potenzialdifferenz Δ Φi = Φi - Φi-1	amortisierte Kosteni = Kosteni + Δ Φi
[None]	0	1	-	-	-	-1	-	-
[a]Array ist voll!	1	1	1	1	1	1	2	3
[a,b]Array ist voll!	2	2	1 + 1	3	3/2	2	1	3
[a,b,c,None]	3	4	2 + 1	6	6/3	2	0	3
[a,b,c,d]Array ist voll!	4	4	1	7	7/4	4	2	3
[a,b,c,d,e,None,None,None]	5	8	4 + 1	12	12/5	2	-2	3
[a,b,c,d,e,f,None,None]	6	8	1	13	13/6	4	2	3
[a,b,c,d,e,f,g,None]	7	8	1	14	14/7	6	2	3
[a,b,c,d,e,f,g,h]Array ist voll!	8	8	1	15	15/8	8	2	3
[a,b,c,d,e,f,g,h,j,None,None,None, None,None,None,None,None,None]	9	16	8 + 1	24	24/9	2	-6	3