Effizienz

(Vorlesung 7.5.:)

Laufzeit

Die Laufzeit ist für den Benutzer ein wichtiges Kriterium. Schwierigkeit bei der Bestimmung: Die Laufzeit hängt von vielen Faktoren ab die evtl. nicht kontrollierbar sind:

• Prozessor/Auslastung des Systems
• Speicher/Cache/Bus
• Compiler/Optimierer des Compilers (Compiler auf verschiedene Architekturen optimiert?)
• Geschick des Programmierers
• Daten (Beispiel Quicksort: Best case und worst case[Vorsortierter Input] stark unterschiedlich)

All diese Faktoren sind untereinander abhängig.

Laufzeitvergleiche sind mit Vorsicht zu interpretieren. Generell sollten bei Vergleichen möglichst wenige Parameter verändert werden, z.B.

• gleiches Programm(gleiche Kompilierung), gleiche Daten, andere Prozessoren

oder

• gleiche CPU, Daten, andere Programme (Vergleich von Algorithmen)

Beobachtung: Durch Laufzeitmessung ist schwer festzustellen, ob ein Alg prinzipiell besser ist als ein anderer.

Komplexität

Komplexitätsbetrachtungen ermöglichen den Vergleich der prinzipiellen Eigenschaften von Algorithmen unabhängig von einer Implementation, Umgebung etc.

Eine einfache Möglichkeit ist das Zählen der Aufrufe einer Schlüsseloperation. Beispiel Sortieren:

• Anzahl der Vergleiche
• Anzahl der Vertauschungen

Beispiel: Selection Sort

 for i in range(len(a)-1):
   max = i
   for j in range(i+1, len(a)):
     if a[j] < a[max]:
       max = j
   a[max], a[i] = a[i], a[max]      # swap

• Anzahl der Vergleiche: Ein Vergleich in jedem Durchlauf der inneren Schleife. Es ergibt sich folgende Komplexität:

  Ingesamt <math>\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1}1 = \frac{N}{2} (N-1) \!</math> Vergleiche.

• Anzahl der Vertauschungen: Eine Vertauschung pro Durchlauf der äußeren Schleife:

  Insgesamt <math>N-1 \!</math> Vertauschungen

Die Komplexität wird durch die Operationen bestimmt, die am häufigsten ausgeführt werden, hier also die Anzahl der Vergleiche. Die Anzahl der Vertauschungen ist kein geeignetes Kriterium für die Komplexität von selection sort, weil der Aufwand in der inneren Schleife ignoriert wird.

Fallunterscheidung: Worst und Average Case

Die Komplexität ist in der Regel eine Funktion der Eingabegröße (Anzahl der Eingabebits, Anzahl der Eingabeelemente). Sie kann aber auch von der Art der Daten abhängen, nicht nur von der Menge, z.B. vorsortierte Daten bei Quicksort. Um von der Art der Daten unabhängig zu werden, kann man zwei Fälle der Komplexität unterscheiden:

• Komplexität im ungünstigsten Fall

  Der ungünstigste Fall ist die Eingabe gegebener Länge, für die der Algorithmus am langsamsten ist. Der Nachteil dieser Methode besteht darin, dass dieser ungünstige Fall in der Praxis vielleicht gar nicht oder nur selten vorkommt, so dass sich der Algorithmus in Wirklichkeit besser verhält als man nach dieser Analyse erwarten würde. Beim Quicksort-Algorithmus mit zufälliger Wahl des Pivot-Elements müsste z.B. stets das kleinste oder größte Element des aktuellen Intervalls als Pivot-Element gewählt werden, was äußerst unwahrscheinlich ist.

• Komplexität im durchschnittlichen/typischen Fall

  Der typische Fall ist die mittlere Komplexität des Algorithmus über alle möglichen Eingaben. Dazu muss man die Wahrscheinlichkeit jeder möglichen Eingabe kennen, und berechnet dann die mittlere Laufzeit über dieser Wahrscheinlichleitsverteilung. Leider ist die Wahrscheinlichkeit der Eingaben oft nicht bekannt, so dass man geeignete Annahmen treffen muss. Bei Sortieralgorithmen können z.B. alle möglichen Permutationen des Eingabearrays als gleich wahrscheinlich angenommen werden, und der typische Fall ist dann die mittlere Komplexität über alle diese Eingaben. Oft hat man jedoch in der Praxis andere Wahrscheinlichkeitsverteilungen, z.B. sind die Daten oft "fast sortiert" (nur wenige Elemente sind an der falschen Stelle). Dann verhält sich der Algorithmus ebenfalls anders als vorhergesagt.

Wir beschränken uns in dieser Vorlesung auf die Komplexität im ungünstigseten Fall. Exakte Formeln für Komplexität sind aber auch dann schwer zu gewinnen, wie das folgende Beispiel zeigt:

Beispiele aus den Übungen (Gemessene Laufzeiten für Mergesort/Selectionsort)

• Mergesort: <math>\frac{0,977N\log N}{\log 2} + 0,267N-4.39 \!</math>

  andere Lösung: <math>1140 N\log(N) - 1819N + 6413 \!</math>

• Selectionsort: <math>\frac{1}{2}N^2 - \frac{1}{2N} - 10^{-12} \!</math>

  andere Lösung: <math>1275N^2 - 116003^N + 11111144 \!</math>

Aus diesen Formeln wird nicht offensichtlich, welcher Algorithmus besser ist. Näherung: Betrachte nur sehr große Eingaben (Meist sind alle Algorithmen schnell genug für kleine Eingaben). Dieses Vorgehen wird als Asymptotische Komplexität bezeichnet (N gegen unendlich).

Asymptotische Komplexität am Beispiel Polynom

Polynom: <math>ax^2+bx+c=p\!</math>

<math>x \!</math> sei die Eingabegröße, und wir betrachten die Entwicklung von <math>p \!</math> in Abhängigkeit von <math>x \!</math>.

• <math>x=0 \!</math>

  <math>p=c \!</math>

• <math>x=1 \!</math>

  <math>p=a+b+c \!</math>

• <math>x=1000 \!</math>

  <math>p=1000000a+1000b+c \approx 1000000a\!</math>

• <math>x \to \infty \!</math>

  <math>p \approx x^2a\!</math>

Für sehr große Eingaben verlieren also b und c immer mehr an Bedeutung, so dass am Ende nur noch a für die Komplexitätsbetrachtung wichtig ist.

O-Notation

• Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme.
• Formale Definition:

  Asymptotische Komplexität: Für zwei Funktionen f(x) und g(x) definiert man

  <math>f(x) \in \mathcal{O}(g(x))</math>

  (sprich "f ist in \mathcal{O}(g)" oder "f ist von derselben Größenordnung wie g") genau dann wenn es eine Konstante <math>c</math> und ein Argument <math>x_0</math> gibt, so dass

  <math>\forall x > x_0:\quad f(x) \le c g(x)</math>.

  Die Idee hinter dieser Definition ist, dass g(x) eine wesentlich einfachere Funktion ist als f(x), die sich aber nach geeigneter Skalierung (Multiplikation mit c) und für große Argumente x im wesentlichen genauso wie f(x) verhält. Man kann deshalb in der Algorithmenanalyse f(x) durch g(x) ersetzen. <math>f(x) \in \mathcal{O}(g(x))</math> spielt für Funktionen eine ähnliche Rolle wie der Operator ≤ für Zahlen: Falls a ≤ b gilt, kann bei einer Abschätzung von oben ebenfalls a durch b ersetzt werden.

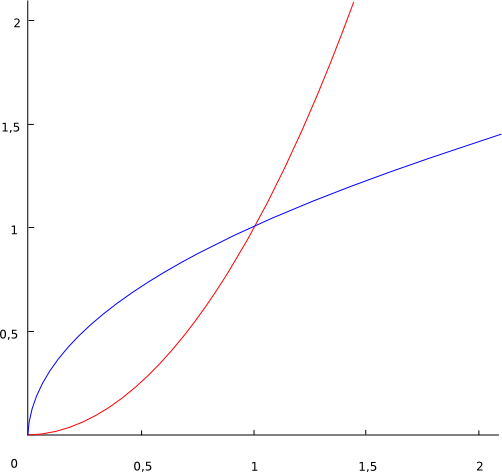
Ein einfaches Beispiel

Rot = <math>x^2 \!</math> Blau = <math>\sqrt{x} \!</math>

<math>\sqrt{x} \in \mathcal{O}(x^2)\!</math> weil <math>\sqrt{x} \le c x^2\!</math> für alle <math>x < x_0 = 1 \!</math> und <math>c = 1\!</math>, oder auch für <math>x < x_0 = 4 \!</math> und <math>c = 1/16</math> (die Wahl von c und x₀ in der Definition von O(.) ist beliebig, solange die Bedingungen erfüllt sind).

Komplexität bei kleinen Eingaben

Algorithmus 1: <math>\mathcal{O}(N^2) \!</math> Algortihmus 2: <math>=\mathcal{O}(N\log{N}) \!</math>

Algorithmus 2 ist schneller (Von geringerer Komplexität), aber bei vielen wiederholten kleinen Eingaben ist Algorithmus 1 schneller.

Eigenschaften der O-Notation(Rechenregeln)

1. Transitiv:

   <math>f(x) \in \mathcal{O}(g(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) \in \mathcal{O}(h(x)) \!</math>

2. Additiv:

   <math>f(x) \in \mathcal{O}(h(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) + g(x) \in \mathcal{O}(h(x)) \!</math>

3. Für Monome gilt:

   <math>x^k \in \mathcal{O}(x^k)) \land x^k \in \mathcal{O}(x^{k+j}), \forall j \ge 0 \!</math>

4. Multiplikation mit einer Konstanten:

   <math>f(x) \in \mathcal{O}(g(x)) \to cf(x) \in \mathcal{O}(g(x))\!</math>

   andere Schreibweise:

   <math>f(x) = cg(x) \to f(x) \in \mathcal{O}(g(x))\!</math>

   Beispiel: <math>ax^2+bx+c \in \mathcal{O}(x^2)\!</math>

   Folgerung für Polynome: <math>a_0+a_1x + ... + a_nx^n \in \mathcal{O}(x^n)\!</math>

5. Logarithmus:

   <math>a, b \neq 1\!</math>

   <math>\log_{a}{x} \in \mathcal{O}(\log_{b}{x})\!</math>

   Die Basis des Logarithmus spielt also keine Rolle.

   Beweis hierfür:

   <math>\log_{a}{x} = \frac{\log_{b}{x}}{\log_{b}{a}}\!</math>

   <math>c = \log_{b}{a}\!</math>

   <math>c\log_{a}{x} = \log_{b}{x}\!</math>, wird hier die Regel für Multiplikation mit einer Konstanten angewendet fällt der Konstante Faktor weg.

   Insbesondere gilt auch <math>\log_{a}{x} \in \mathcal{O}(\log_{2}{x})\!</math>, es kann also immer der 2er Logarithmus verewendet werden.

O-Kalkül

1. <math>f(x) \in \mathcal{O}(f(x))\!</math>
2. <math>\mathcal{O}(\mathcal{O}(f(x))) \in \mathcal{O}(f(x))\!</math>
3. <math>k\mathcal{O}(f(x)) \in \mathcal{O}(f(x))\!</math>
4. <math>\mathcal{O}(f(x))+c \in \mathcal{O}(f(x))\!</math>
5. Sequenzregel:

   <math>g(x) \in \mathcal{O}(f(x)) \to \mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(f(x))\!</math>, oder <math>f(x) \in \mathcal{O}(g(x)) \to \mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(g(x))\!</math>

   Informale Schreibweise: <math>\mathcal{O}(max(f(x), (g(x))\!</math>

6. Aufruf, Verschachtelungsregel:

   <math>\mathcal{O}(f(x)) * \mathcal{O}(g(x)) \in \mathcal{O}(f(x) * g(x))\!</math>

O-Kalkül auf das Beispiel des Selectionsort angewandt

Selectionsort: <math>f(N) = \frac{N^2}{2} - \frac{N}{2} \in \mathcal{O}(\frac{N^2}{2}) \in \mathcal{O}(N^2)\!</math>

Oder via Multiplikationsregel: <math>\mathcal{O}(f(x))*\mathcal{O}(g(x)) \in \mathcal{O}(f(x)*g(x))\!</math>

Äußere Schleife: <math>\mathcal{O}f(x)\!</math>

<math>f(N) = N/2 = \mathcal{O}(N)\!</math>

Innere Schleife: <math>\mathcal{O}g(x)\!</math>

<math>g(N) = N-2 = \mathcal{O}(N)\!</math>

<math>\mathcal{O}(f(N))*\mathcal{O}(g(N)) \in \mathcal{O}(f(x)*g(x))\!</math>

<math>\mathcal{O}(N)*\mathcal{O}(N) \in \mathcal{O}(N*N) \in \mathcal{O}(N^2)\!</math>

Nach beiden Vorgehensweisen erreichen wir also den Schluss, dass der Selectionsort die asymptotische Komplexität <math>\mathcal{O}(N^2)\!</math> besitzt.

Zusammenhang zwischen Komplexität und Laufzeit

Wenn ein Rechenschritt 1ms dauert erreichen verschiedene komplexe Algorithmen folgende Leistungen

Komplexität	Operationen in 1s	Operationen in 1min	Operationen in 1h
<math>\mathcal{O}(N)</math>	1000	60.000	3.600.000
<math>\mathcal{O}(n\log{N})</math>	140	4895	204094
<math>\mathcal{O}(N^2)</math>	31	244	1897
<math>\mathcal{O}(N^3)</math>	10	39	153
<math>\mathcal{O}(2^N)</math>	9	15	21

Exponentielle Komplexität

Der letzte Fall (<math>\mathcal{O}(2^N)</math>) ist von exponentieller Komlexität, das bedeutet eine Verdopplung des Aufwands bewirkt nur, dass die maximale Problemgröße um eine Konstante wächst. Algorithmen mit exponentieller Komplexität heißen ineffizient.

Dagegen bewirkt bei einer Komplexität von <math>\mathcal{O}(N^3)</math> ein verdoppelter Aufwand immer noch eine Steigerung der maximalen Problemgörße um den Faktor <math>\sqrt[3]{2}</math>.

(Vorlesung 8.5.)

(noch in Arbeit!!!)

Beispiel: running Average

Version 1	Version 2
r = [0] * len(a) if k > len(a): raise RuntimeError("k zu groß") for j in range(k, len(a)) for i in range(j-k+1, j+1) r[j] += a[i] r[j] /= float(k) return r	if k > len(a): raise RuntimeError ("k zu groß") r = [0] * len(a) for i in range(k) r[k] += a[i] for j in range(k+1, len(a)): r[j] += (a[j]-a[j-k]+r[j-1] for j in range(len(a)): r[j] /= float(k) return r