Prioritätswarteschlangen

Sortieren als Suchproblem

Systematisches Fragen mit True und False kann auch als Baum dargestellt werden.

Hier ein Beispiel.Als Eingabe sind drei Zahlen angegeben a={1,2,3},wobei die Reihenfolge nicht bekannt ist.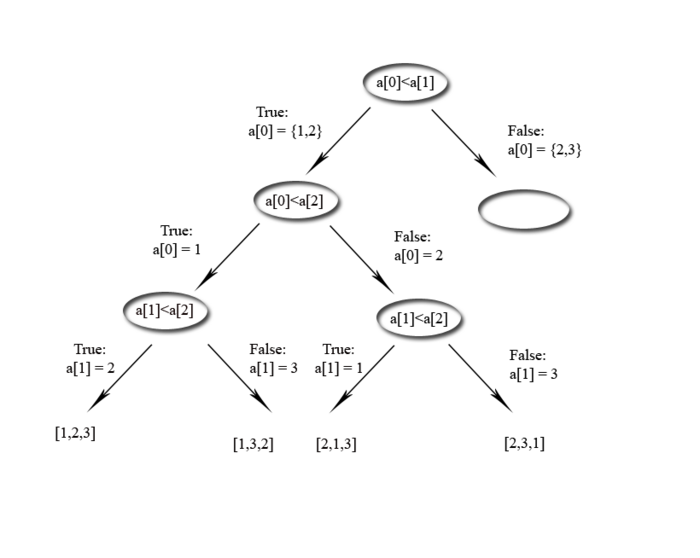

Also mit Eingabe von drei Elemnten müssen im ungünstigsten Fall drei Schritte vorgenommen werden.
Die allgemeine Regel lautet: es gibt N mögliche Lösungen
=>der Baum muss N Blätter haben
=>ein baum mit N Blättern hat mindestens die Höhe logN

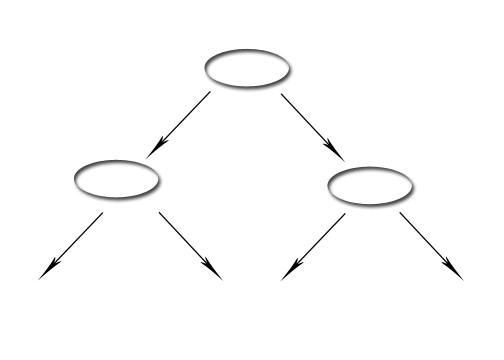
vollständiger Baum (oder balancierter Baum)[1]
2^d+1 Knoten
2^d Blätter

Sortieren

N = n!wenn das Arrey n Elemente hat
Zum Beispiel: 3! = 1*2*3 = 6
log6 <math>\approx</math> 2,6 => d = 3 - bei dem Frage-Baum brauch man im ungünstigsten Fall drei Schritte (True/False)
log6 <math>\approx</math> 2,6 - weil nicht jeder Pfad zu Ende durchgelaufen sein soll, um die Lösung zu bekommen.
d<math>\ge</math>log<math>_2</math>n! = log<math>_2</math>(1,2...n) = log<math>_2</math>1 + log<math>_2</math>2 + ... + log<math>_2</math>n = <math>\sum_{n=1}^n log_2n </math>

Abschätzung von Summen durch Integrale

gegeben : f(x) - monoton wachsend

<math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lfloor x \big\rfloor)dx</math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(x)dx </math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lceil x \big\rceil)dx</math>

<math>\downarrow</math>

<math>\textstyle \int\limits_{x_1}^{x_1 + 1} \underline{f(x_1)}dx</math> + ...+ <math>\textstyle \int\limits_{x_2-1}^{x_2} f(x_2 - 1)dx </math> = <math>\sum_{k=x_1}^{x_2-1} f(k)</math>
( angenommen <math>x_1</math> und <math>x_2</math> <math>\in </math> <math>\mathbb{N},\mathbb{Z}</math> )

wobei f(<math>x_1</math>) = f(<math>\big\lfloor x \big\rfloor </math><math>)_{x_1}^{x_1 +1}</math>

<math>\textstyle \int\limits_{x_1}^{x_1 +1} f(x_1)dx</math> = f(<math>x_1</math>) <math>\textstyle \int\limits_{x_1}^{x_1 + 1} 1dx</math> = f(<math>x_1</math>)x<math>\textstyle \int\limits_{x_1}^{x_1 + 1}</math> = f(x_1)

<math>\sum_{k=x_1}^{x_2-1} f(k) \le \textstyle \int\limits_{x_1}^{x_2} f(x)dx</math>

<math>\sum_{k=x_1 +1}^{x_2} f(k) \ge \textstyle \int\limits_{x_1}^{x_2} f(x)dx \iff</math> <math>\sum_{k=x_1}^{x_2} f(x) \ge \textstyle \int\limits_{x_1 - 1}^{x_2} f(x)dx </math>

für uns gilt: f(x) = log<math>_2</math>(x)

log<math>_2</math>1 + <math>\sum_{k=2}^{n} log_2 x\ge\textstyle \int\limits_{1}^{n} log_2 (x)dx </math> = <math>\frac{1}{ln2}\textstyle \int\limits_{1}^{n} log(x)dx</math> = <math>\frac{1}{ln2}</math> [xlogx - x]<math>_{x = 1}^n</math> = nlog<math>_2</math>(n) - <math>\frac{n - 1}{ln2}</math> = <math>\Omega</math>(nlog<math>_2</math>n)

<math>\Rightarrow</math> d = log<math>_2</math>n! = <math>\Omega</math>(nlogn)

kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymthotisch schneller als Mergesort

Prioritätswarteschlangen

* Max Priority Quene : insert(x)
                      x = largest()
                      removeLargest()

* Min Priority Quene: smallest()
                     REMOVEsMALLEST()

Prioritätswarteschlange als Suchproblem

• Sequentielle Suche - Array mit Prioritäten : insert(x)<=> a.append(x) ( <math>\mathcal{O}(1)</math>(amortisierte Komplexität))

def largest(a):

   if len (a) == 0:  

       raise RuntimeError("...")

    max = a[0]

    k = 0

    for n in range(1, len(a):             (innere Schleife von SelectionSort)

       if a[n] > max                       (Das ganze hat die Komplexität: N = len(a) => <math>\mathcal{O}(N)</math>

           man = a[n]

               k = n

    return k

Bei kleine Array ist dies die schnellste Methode

Binärer (balancierter)Suchbaum

insert => z.B. wie beim Anderson Baum [2] <math>\mathcal{O}(logN)</math>

def largest(node):                     # Wurzel

   if node.right is not None:    #rechts stehen immer  die großen

       return largest(node.right)

   return node                   #wenn es nicht mehr nach rechts geht, dann haben wir den größten Knoten gefunden

Das ganze hat <math>\mathcal{O}(logN)</math> Komplexität
Ergebnis: gute Komplexität aber komplizierte Datenstruktur

Heap

• Datenstruktur optimiert für Prioritätssuche - man sucht nicht effizient alle Knoten, sondern nur einen bestimmten z.B. Heap max
  
• Definition: ein linkslastiger Binärbaum ist ein Baum mit <math>d(node.left) \geq d(node.right)</math>

Ein Heap ist ein linkslastiger, perfekt balancierter Baum. (lässt sich max. um 1 unterscheiden)

Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht:

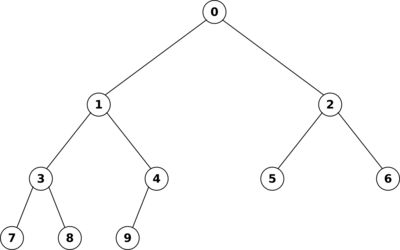
index[parent] = [(indexChild - 1)/2]   #[] heißt abgerundet

index[left] = index[parent]2 + 1

index[right] = index[parent]2 + 2

=> linkslastiger perfect balancierter Binärbaum kann effizient als Array abgespeichert werden
=>verwende Indezies wie oben

Heap - Bedingung

• die Wurzel hat höhere Prioriät als die Kinder(gilt für jeden Teilbaum)
  

=>Wurzel = array[0] hat die größte Priorität

def largest(h):

    return h[0]        <math>\mathcal{O}(N)</math>

Einfügen in einem Heap

h - Array #speichrt Haep

 def insert(h,x):

     h.append(x)  # wir speichern den Wurzel am Ende, so wird glecih zu einem linkssalstigen perfect balancierten Baum (die Haep - Bedingung ist erfüllt)

     upheap(h, len(h) - 1):

def upheap(h, k):

   """k-tes Element evtl. an der falsche Stelle

   """

   v = h[k]

   while True      #endlose Schleife
        
       if k == 0:

           break

       parent = (k - 1/2)

       if h[parent]>v:

           break

       h[k] = h.parent

       k = parent

       h[k] = v

def removeLargest(h):
    h[0] = h[len(h) - 1]

    del h[len(n) - 1]              <math>\mathcal{O}(1)</math>

    downHeap(h, 0)                       <math>\mathcal{O}(logN)</math>

def downHeap(h, k):

    v = h[k]

    while True

        child = 2k + 1              #linke Kind

        if child <math>\ge</math>len{h):

              break

        if child < and h[child] < h[child + 1]         #rechtes Kind

              child = child + 1
        if v <math>\ge</math> h[child]:

              break

        h[k] = h[child]

        k = child

   h[k] = v