Prioritätswarteschlangen: Difference between revisions
From Alda
Jump to navigationJump to search
(heap - first edit) |
m (→Heap: Größe der Grafik geändert) |
||
| Line 7: | Line 7: | ||
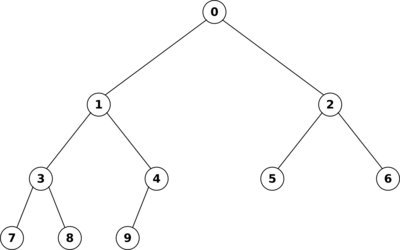
Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht: | Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht: | ||
[[Image:heapArray.png]] | [[Image:heapArray.png|left|400px]] | ||
Revision as of 11:44, 28 May 2008
Prioritätswarteschlangen
Heap
- Datenstruktur optimiert für Prioritätssuche
- Def: ein linkslastiger Binärbaum ist ein Baum mit <math>d(node.left) \geq d(node.right)</math>
Ein Heap ist ein linkslastiger, perfekt balancierter Baum.
Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht: