Hashing und assoziative Arrays: Difference between revisions
| (62 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
Mitschrift gibts [http://hci.iwr.uni-heidelberg.de/alda/images/AlDa.pdf | Die Mitschrift gibts auch als [http://hci.iwr.uni-heidelberg.de/alda/images/AlDa.pdf PDF]. | ||
== Assoziative Arrays == | == Assoziative Arrays == | ||
Assoziative Arrays werden genau wie gewöhnliche Arrays benutzt, sie unterstützen also den lesenden | Assoziative Arrays werden genau wie gewöhnliche Arrays benutzt, sie unterstützen also den lesenden und schreibenden Zugriff über einen Index i | ||
X = a[i] | X = a[i] | ||
a[i] = x | a[i] = x | ||
Im Unterschied zum gewöhnlichen Array, wo i ein Integer im Bereich <math> i \in 0 \ldots N-1</math> sein muss, kann der Typ von i jetzt ''beliebig'' sein. Eine typische Anwendung ist ein Wörterbuch | Im Unterschied zum gewöhnlichen Array, wo i ein Integer im Bereich <math> i \in 0 \ldots N-1</math> sein muss, kann der Typ von i jetzt ''beliebig'' sein. Eine typische Anwendung ist ein Wörterbuch | ||
x = toEnglish['Baum'] # ergibt 'tree' | x = toEnglish['Baum'] # ergibt 'tree' | ||
In diesem Fall ist der Typ des Index <tt>string</tt>, was in der Praxis der häufigste Fall ist, weshalb assoziative Arrays oft als ''Dictionary'' bezeichnet werden (so auch in Python, hier heißt der Typ <tt>dict</tt>). Im allgemeinen kann aber jeder Typ als Index benutzt werden, für den entweder eine Ordnung oder eine Hashfunktion definiert ist. | In diesem Fall ist der Typ des Index <tt>string</tt>, was in der Praxis der häufigste Fall ist, weshalb assoziative Arrays oft als ''Dictionary'' bezeichnet werden (so auch in Python, hier heißt der Typ <tt>dict</tt>). Im allgemeinen kann aber jeder Typ als Index benutzt werden, für den entweder eine Ordnung oder eine Hashfunktion definiert ist. Im ersten Fall realisiert man das assoziative Array mit Hilfe eines Suchbaums, im zweiten Fall mit Hilfe einer Hashtabelle. | ||
==Realisierung des assoziativen Arrays als Suchbaum== | ==Realisierung des assoziativen Arrays als Suchbaum== | ||
| Line 32: | Line 27: | ||
self.root = None | self.root = None | ||
self.size = 0 | self.size = 0 | ||
Die Funktion <tt>__setitem__</tt> schaut nach, ob ein Eintrag mit dem betreffenden Index bereits existiert. Wenn ja, werden seine Daten mit den neuen Daten überschrieben, andernfalls wird ein neuer Eintrag angelegt. Intern werden dazu die bereits bekannten Funktionen <tt>treeSearch</tt> | Die Funktion <tt>__setitem__</tt> schaut nach, ob ein Eintrag mit dem betreffenden Index bereits existiert. Wenn ja, werden seine Daten mit den neuen Daten überschrieben, andernfalls wird ein neuer Eintrag angelegt. Intern werden dazu die bereits bekannten Funktionen <tt>treeSearch</tt> und <tt>treeInsert</tt> verwendet (siehe Abschnitt [[Suchen#Suchbäume|Suchbäume]]): | ||
def __setitem__(self, index, | def __setitem__(self, index, data): | ||
node = treeSearch(self.root, index) | node = treeSearch(self.root, index) | ||
if node is None: | if node is None: | ||
| Line 44: | Line 39: | ||
node = treeSearch(self.root, index) | node = treeSearch(self.root, index) | ||
if node is None: | if node is None: | ||
raise KeyError( | raise KeyError(index) | ||
else: | else: | ||
return node.data | return node.data | ||
Die Indexoperationen haben bei der Realisierung mit Baumsuche eine Komplexität in O(log n). | Die Indexoperationen haben bei der Realisierung mit Baumsuche eine Komplexität in O(log n). | ||
Ein wichtiges Beispiel für ein assoziatives Array, das auf diese Weise realisiert wurde, ist die C++ Standardklasse <tt>std::map</tt>. | Ein wichtiges Beispiel für ein assoziatives Array, das auf diese Weise realisiert wurde, ist die C++ Standardklasse <tt>[http://www.sgi.com/tech/stl/Map.html std::map]</tt>. | ||
== Hashing == | == Hashing == | ||
| Line 57: | Line 52: | ||
===Hashfunktionen=== | ===Hashfunktionen=== | ||
Gegeben sei ein Universum U, dass die Menge aller legalen Schlüssel darstellt. Die | Gegeben sei ein Universum U, dass die Menge aller legalen Schlüssel darstellt. Die Mächtigkeit |U| der Menge U ist im allgemeinen sehr groß. Beispielsweise kann man mit Strings der Länge 9 bis zu 27<sup>9</sup>≈10<sup>13</sup>≈2<sup>43</sup> verschiedene Schlüssel generieren, wenn 27 Zeichen erlaubt sind (Kleinbuchstaben und Leerzeichen). Die Grundannahme von Hashing ist jetzt, dass in jeder gegebenen Anwendung nur ein (kleiner) Teil der erlaubten Schlüssel tatsächlich verwendet wird. Man definiert eine Hashfunktion, die jeden Schlüssel auf eine natürliche Zahl im Bereich 0...(M-1) abbildet, wobei M viel kleiner als |U| ist. | ||
;Hashfunktion: | ;Definition einer Hashfunktion: | ||
:::<math> f: | :::<math> f: U \rightarrow [0, 1, \ldots, M-1] \subset \mathbb{N} </math> | ||
Da M < |U|, werden notwendigerweise einige Schlüssel auf dieselbe Zahl abgebildet. Man bezeichnet den Fall <math> f(u_1 \in U) = f(u_2 \in U) </math> als ''Kollision'' zwischen den | :::<math> f(u \in U) = h \in [0, 1, \ldots, M-1]</math> | ||
h wird als ''Hashwert'' von u bezeichnet. Da M < |U|, werden notwendigerweise einige Schlüssel auf dieselbe Zahl abgebildet. Man bezeichnet den Fall <math> f(u_1 \in U) = f(u_2 \in U) </math> als ''Kollision'' zwischen den Schlüsseln u<sub>1</sub> und u<sub>2</sub>. | |||
Die '''Aufgabe''' besteht jetzt darin, ein Hash-Funktion zu entwerfen, die möglichst wenige Kollisionen hat. Hashfunktionen ähneln damit einem Zufallszahlengenerator, weil jede Zahl <math> h \in 0 \ldots (M-1) </math> nach Möglichkeit mit gleicher Wahrscheinlichkeit herauskommen soll. Wird dieses Ziel erreicht, spricht man vom ''uniformen Hashing''. | |||
In der Regel ist aber nicht vorher bekannt, welche Schlüssel in einer Anwendung verwendet werden. Es kann deshalb immer vorkommen, dass die verwendete Schlüsselmenge sehr viele Kollisionen verursacht. Man sieht in der Tat leicht ein, dass für jede gegebene Hashfunktion ungünstige Schlüsselmengen <math> U_f \subset U</math> existieren, bei denen es sehr viele Kollisionen gibt. Im ungünstigsten Fall könnte U<sub>f</sub> so gewählt sein, dass f(U<sub>f</sub>) = k = const. gilt. Ein Hacker, der die verwendete Hashfunktion kennt, kann z.B. U<sub>f</sub> absichtlich so wählen, um eine denial-of-service-Attacke gegen einen hash-basierten Webservice zu starten. Ein anderes anschauliches Beispiel wäre eine Party, zu der nur Leute eingeladen werden, die an einem 8ten im Monat Geburtstag haben. Auf dieser Party ist es viel wahrscheinlicher, Leute zu finden, die am selben (oder gleichen) Tag Geburtstag haben, als wenn man alle einlädt. | |||
D.h. die Wahl einer guten Hashfunktion ist eine Kunst, und man muss (wenn möglich) die Daten analysieren um ein gutes f zu finden. | |||
====Perfektes Hashing==== | |||
Kennt man die Untermenge der tatsächlich vorkommenden Schlüssel <math>U_f \subset U</math> schon im voraus, hat man die Möglichkeit, eine ''perfekte Hashfunktion'' ohne Kollisionen zu entwerfen. | |||
;Beispiel anhand der Monatsnamen | |||
U ist in diesem Fall eine Menge von Strings der Länge 9 (weil der September als längster Monatsname 9 Zeichen hat). Es ergeben sich also <math>60^{9}</math>>≈10<sup>16</sup>≈2<sup>54</sup> mögliche Strings, da mit Groß- und Kleinbuchstaben, Umlauten, ß und Leerzeichen 60 Zeichen im deutschen Alphabet vorhanden sind. Von all diesen Möglichkeiten werden genau 12 benutzt: | |||
:::<math>U_f</math> = {"Januar"; "Februar"; ... ; "Dezember"} | |||
<math> | * Benutzt man nun als Hashfunktion die Anfangsbuchstaben der Monatsnamen, benötigt man dafür 6 bit. M ist somit 64. | ||
<math> | :::{"Januar"; "Februar"; ... ; "Dezember"} → {"J"; "F"; "M"; "A"; "M"; "J"; "J"; "A"; "S"; "O"; "N"; "D"} | ||
* | :Dabei enstehen viele Kollisionen (J wird 3x verwendet, M 2x, A 2x), die gewählte ist also keine gute Hashfunktion | ||
* | * Benutzt man als Hashfunktion die ersten 3 Buchstaben benötigt man 18 bit, M = <math>2^{18}</math> | ||
:::{"Januar"; "Februar"; ... ; "Dezember"} → {"Jan", "Feb", "März", "Apr", "Mai", "Jun", "Jul", "Aug", "Sep", "Okt", "Nov", "Dez"} | |||
:Nun entstehen keine Kollision mehr. Diese Hashfunktion ist deshalb beim Ausfüllen von Formularen und dergleichen sehr beliebt. Dafür ist M aber recht groß. | |||
Die Aufgabe wird also präzisiert: man sucht für <math>U_f</math> eine '''minimale, perfekte Hashfunktion''', für die <math>|U_f| = M</math> gilt. Ein Verfahren hierfür ist Gegenstand von Übungsblatt 9. | |||
====Universelles Hashing==== | |||
Hier wählt man für eine gegebene Hashtabelle die Hashfunktion per Zufallszahl aus einer (großen) Menge erlaubter Hashfunktion → Die Wahrscheinlichkeit, dass die Hashfunktion für die Schlüssel ungünstig ist, wird dadruch minimiert. Die oben erwähnte denial-of-service-Attacke ist jetzt nicht mehr möglich, weil kein Hacker die Hashfunktion im voraus kennen kann. Näheres zum universellen Hashing finden Sie in der [http://en.wikipedia.org/wiki/Universal_hashing Wikpedia]. | |||
====Kryptographische Hashfunktionen==== | |||
In kryptographischen Anwendungen treten neben dem Hauptziel, die Größe des Universums auf eine überschaubare Zahl von Integer-Werten zu reduzieren, zwei weitere Anforderungen, die für Verschlüsselung bzw. verschlüsselte Kommunikation wichtig sind: erstens will man Kollisionen unbedingt vermeiden (damit zwei verschiedene Dokumente oder Passwörter nicht auf den gleichen Hashwert abgebildet werden), und zweitens darf es nicht möglich sein, aus dem Hashwert die urpsrüngliche Nachricht (also das Dokument oder Passwort) zu rekonstruieren. Man wählt deshalb relative große M (128 bit und mehr) sowie spezielle, für diesen Zweck optimierte Hashfunktionen, wie z.B. [http://de.wikipedia.org/wiki/Message-Digest_Algorithm_5 md5] und [http://de.wikipedia.org/wiki/SHA1 sha1]. Weitere Einzelheiten finden Sie in der [http://en.wikipedia.org/wiki/Cryptographic_hash_function Wikipedia]. | |||
====Beliebte Standard-Hashfunktionen==== | |||
=== | In der Praxis definiert man Hashfunktionen gewöhnlich zweistufig: Zunächst bildet man den Schlüssel auf einen 32 bit Integerwert ab, M' ist damit 2<sup>32</sup>. Dieser "rohe" Hashwert wird dann mittels der Modulo-Operation auf die eigentliche Größe M des assoziativen Arrays abgebildet: | ||
Kollisionen | :::<math> f(u \in U) = f'(u \in U)\,\%\,M\,=\,h \in [0, 1, \ldots, M-1] </math> | ||
mit | |||
:::<math> f'(u \in U) = h' \in [0, 1, \ldots, 2^{32}-1] </math> | |||
Der große Wert von M' sichert, dass man bei der Wahl von M großen Spielraum hat, so dass die Größe des assoziativen Arrays sehr gut an die Menge der zu speichernden Daten angepaßt werden kann. Die Funktion f'(u) definiert man wie folgt: | |||
* Falls U = <tt>unsigned int</tt> (32bit int Datentyp) ⇒ f'(u) = u | |||
* Falls U = <tt>signed int</tt> ⇒ Typkonvertierung nach <tt>unsigned int</tt> ⇒ f'(u) = (unsigned int)u | |||
* Andere Schlüsseltypen (also insbesondere Strings) interpretiert man als Array of byte ⇒ f'(u) konvertiert Array of Byte nach <tt>unsigned int</tt>. Beispiele für solche Funktionen: | |||
:: '''Bernsteinfunktion:''' | |||
def bHash(u): # u: Array of Byte | |||
h=0 | |||
for k in u: | |||
h = 33 * h + k | |||
return h | |||
:: '''modifizierte Bernsteinfunktion:''' | |||
def mbHash(u): # u: Array of Byte | |||
h=0 | |||
for k in u: | |||
h = (33 * h) ^ k # ^ ist bitweises Xor | |||
return h | |||
:: '''Shift-Add-Xor-Funktion:''' | |||
def saxhash(u): # u: Array of Byte | |||
h=0 | |||
for k in u: | |||
h ^= (h << 5) + (h >> 2) + k # << und >> sind Links- bzw. Rechtsshift der Bits, ^= ist bitweise Xor-Zuweisung | |||
return h | |||
:: '''Fowler/Noll/Vo-Funktion:''' | |||
def FNVhash(u): # u: Array of Byte | |||
h = 2166136261 | |||
for k in u: | |||
h = (16777619 * h) ^ k # ähnlich der modifizierten Bernsteinfunktion, aber mit anderen Konstanten | |||
return h | |||
:: Die verwendeten Konstanten sind experimentell so gewählt worden, dass die Hashfunktionen in typischen Praxisanwendungen relativ wenige Kollisionen verursachen. Der tiefere Grund, warum z.B. 33 in der Bernsteinfunktion eine gute Wahl darstellt, ist unbekannt. Es empfielt sich, in einer gegebenen Anwendung mit mehreren Hashfunktionen zu experimentieren. Weitere solche Funktionen und andere nützliche Informationen findet man auf der Seite [http://www.eternallyconfuzzled.com/tuts/algorithms/jsw_tut_hashing.aspx eternallyconfuzzled.com]. | |||
== Hashtabellen == | |||
Eine Hashtabelle ist eine Datenstruktur, die die Funktionalität des assoziativen Arrays mit Hilfe von Hashing realisiert. Das Grundprinzip besteht darin, dass die Hashtabelle intern ein (dynamisches) Array der Größe <tt>capacity</tt> verwaltet, so dass die Hashwerte als Indizes in diesem Array verwendet werden können (<tt>capacity</tt> entspricht der Zahl M aus der mathematischen Definition oben). Eine naive Implementation der Einfügeoperation sieht also so aus | |||
def __setitem__(self, key, value): # naive Implementation, funktioniert so nicht | |||
index = self.hash(key) % self.capacity | |||
self.array[index] = value | |||
Diese Implementation ist allerdings zu einfach. Wenn nämlich die Schlüssel aus dem Universum U beliebig gewählt werden dürfen, sind Kollisionen unvermeidlich. Tritt aber eine Kollision auf, werden die Daten eines Schlüssels mit den Daten eines anderen Schlüssels überschrieben. Um Kollisionen geschickt zu behandeln gibt es zwei Ansätze: | |||
* lineare Verkettung | * lineare Verkettung | ||
* offene Adressierung | * offene Adressierung | ||
=== | === Hashtabelle mit linearer Verkettung (offenes Hashing/geschlossene Adressierung) === | ||
Man kann dies als die pessimistische Lösung bezeichnen: Man nimmt an, dass Kollisionen häufig auftreten. Deshalb wird unter jedem | |||
Hashindex gleich eine Liste angelegt, in der Einträge mit gleichem Hashindex aufgenommen werden können. Die Hashtabelle verwaltet ein Array von Listen, und jedes Arrayfeld kann beliebig viele Elemente speichern: Wird ein Element auf den Index <tt>i</tt> abgebildet, werden die Daten einfach an die betreffende Liste angehängt. Bei Zugriff auf ein Element wird zunächst die passende Liste gesucht (mit Hilfe des Hashwerts), danach erfolgt in dieser Liste eine sequentielle Suche nach dem richtigen Schlüssel. | |||
Um diese Idee implementieren zu können, benötigen wir zunächst eine Hilfsklasse <tt>HashNode</tt>, die (Schlüssel, Wert)-Paare speichert und mit Hilfe von <tt>next</tt> eine verkettete Liste realisiert: | |||
und mit Hilfe von | |||
class HashNode: | class HashNode: | ||
def __init__(self,key,data,next): | def __init__(self,key,data,next): | ||
self.key = key | self.key = key | ||
self.data = data | self.data = data | ||
self.next = next # Verkettung! | self.next = next # Verkettung! | ||
Die eigentliche Hashtabelle wird in der Klasse ''HashTable'' implementiert: | Die eigentliche Hashtabelle wird in der Klasse ''HashTable'' implementiert: | ||
class HashTable: | class HashTable: | ||
def __init__(self): | def __init__(self): | ||
self.capacity = ... # Geeignete Werte siehe unten | self.capacity = ... # Geeignete Werte siehe unten | ||
self.size = 0 | self.size = 0 # Anzahl der Werte, die zur Zeit tatsächlich gespeichert sind | ||
self.array = [None]*self.capacity | self.array = [None]*self.capacity | ||
Wie oben bereits erwähnt, werden die Zugriffsoperatoren ''[ ]'' für eine Datenstruktur in Python durch die Funktionen <tt>__setitem__</tt> bzw. <tt>__getitem__</tt> implementiert. | |||
Die <tt>__setitem__</tt>-Funktion speichert die gegebenen Daten unter dem Schlüssel <tt>key</tt> in der <tt>HashTable</tt>-Klasse: | |||
def __setitem__(self, key, value): | |||
index = hash(key) % self.capacity # hash(...) ist in Python eine vordefinierte Funktion | |||
node = self.array[index] # finde die zu 'key' gehörende Liste | |||
while node is not None: # sequentielle Suche nach 'key' in dieser Liste | |||
if node.key == key: | |||
# Element 'key' ist schon in der Tabelle | |||
# => überschreibe die Daten mit dem neuen Wert | |||
node.data = value | |||
return | |||
# andernfalls: Kollision des Hashwerts, probiere nächsten 'key' aus | |||
node = node.next | |||
# kein Element hatte den richtigen Schlüssel. | |||
# => es gibt diesen Schlüssel noch nicht | |||
# füge also ein neues Element in die Hashtabelle ein | |||
self.array[index] = HashNode(key, value, self.array[index]) # der alte Anfang der Liste wird zum | |||
# Nachfolger des neu eingefügten ersten Elements | |||
self.size += 1 | |||
... # eventuell muss jetzt noch die Kapazität optimiert werden | |||
Die Funktion <tt>__getitem__</tt> gibt die unter dem Schlüssel <tt>key</tt> abgelegten Daten zurück, oder eine Fehlermeldung, falls dieser Schlüssel nicht existiert: | |||
def __getitem__(self, key): | |||
index = hash(key) % self.capacity | |||
node = self.array[index] # finde die zu 'key' gehörende Liste | |||
while node is not None: # sequentielle Suche nach 'key' in dieser Liste | |||
if node.key == key: # gefunden! | |||
return node.data # => Daten zurückgeben | |||
node = node.next # nächsten Schlüssel probieren | |||
raise KeyError(key) # Schlüssel nicht gefunden => Fehler | |||
==== Komplexität der linearen Verkettung und Wahl der Kapazität ==== | |||
Die Komplexität wird durch zwei Operationen bestimmt: erstens das Auffinden der zu einem Schlüssel gehörenden Liste (die in O(1) erfolgt), zweitens das sequentielle Durchsuchen der Liste, die Zeit in O(L) erfordert, wobei L die mittlere Länge der Listen ist. Die Hashtabelle ist also nur schnell, wenn die Länge der Listen möglichst klein ist. Unter der Annahme des ''uniformen Hashings'', wenn also alle Indizes gleich häufig verwendet werden, ist L gleich dem '''Füllstand''' der Hashtabelle: | |||
:::<math>\alpha = \frac{N}{M} = \frac{\text{size}}{\text{capacity}}</math> wobei N die Größe <tt>size</tt> der Hashtabelle und M die Größe <tt>capacity</tt> des Arrays ist. | |||
Wenn die Hashwerte uniform sind, entfallen auf jede Liste im Mittel N/M Einträge (N Einträge, verteilt auf M Listen). Die Gesamtkomplexität berechnet sich nach der Sequenzregel zu | |||
:::<math>O(1+\alpha)</math> | |||
Für eine effiziente Suche muss demnach <math>\alpha \in O(1)</math> gewählt werden. Dies erreicht man, indem man, wie beim dynamischen Array, <tt>capacity</tt> immer wieder anpasst, falls <tt>size</tt> zu groß wird. Üblicherweise verdoppelt man <tt>capacity</tt>, sobald <tt>size == capacity</tt> erreicht wird. Analog zum dynamischen Array werden die Daten dann aus dem alten Array (<tt>self.array</tt>) in ein entsprechend vergrößertes neues Array kopiert. | |||
In der C++ Standardbibliothek (Klasse <tt> [http://www.cplusplus.com/reference/stl/unordered_map/ std::unordered_map]</tt>, siehe auch [http://gcc.gnu.org/viewcvs/trunk/libstdc%2B%2B-v3/src/shared/hashtable-aux.cc?view=markup GCC hashtable_aux.cc (Primzahlen)] und [http://gcc.gnu.org/viewcvs/trunk/libstdc%2B%2B-v3/include/bits/hashtable_policy.h?view=markup GCC Hash Implementation]) wird die Hashtabelle häufig so | |||
implementiert. Dabei wird <tt>capacity</tt> immer als ''Primzahl'' gewählt, wobei sich aufeinanderfolgende Kapazitäten immer ungefähr verdoppeln. Dazu wählt man aus einer vorberechneten Liste von Primzahlen die kleinste Zahl, so dass <tT>new_capacity >= 2*capacity</tt> gilt, und beginnt z.B. mit einer Default-Kapazität von 11: | |||
11, 23, 47, 97, 199, 409, 823, ... | |||
Die Wahl von Primzahlen hat zur Folge, dass <tt>hash(key) % self.capacity</tt> ''alle'' Bits von h benutzt (Eigenschaft aus der Zahlentheorie). Die Kapazität wird vergrößert, wenn <tt>size == capacity</tt> erreicht wird, und die ungefähre Verdoppelung sichert, dass die amortisierte Komplexität der Einfügeoperation in O(1) ist (wie beim dynamischen Array). | |||
== Hashtabelle mit offener Adressierung ( | === Hashtabelle mit offener Adressierung (geschlossenes Hashing) === | ||
[[Image:HASHTB12.svg.png|frame|Prinzip ([http://en.wikipedia.org/wiki/Hash_table Quelle])]] | [[Image:HASHTB12.svg.png|frame|Prinzip ([http://en.wikipedia.org/wiki/Hash_table Quelle])]] | ||
[http://de.wikipedia.org/wiki/Hashtabelle#Hashing_mit_offener_Adressierung Wikipedia (de)] | Dies kann als die optimistische Variante betrachtet werden: man nimmt an, dass Kollisionen nicht so häufig auftreten, um eine komplexe Datenstruktur wie das "Array von Listen" zu rechtfertigen. Stattdessen behandelt man Kollisionen mit einer einfachen '''Idee''': Wenn <tt>array[index]</tt> durch Kollision bereits vergeben ist, probiere einen | ||
[http://en.wikipedia.org/wiki/Open_addressing Wikipedia (en)] | anderen Index aus (siehe auch [http://de.wikipedia.org/wiki/Hashtabelle#Hashing_mit_offener_Adressierung Wikipedia (de)] und | ||
[http://en.wikipedia.org/wiki/Open_addressing Wikipedia (en)]). Dabei muss man folgendes beachten: | |||
* Das Array enthält pro Element höchstens ein (key,value)-Paar | |||
* Das Array muss stets mindestens ''einen'' freien Platz haben (sonst gäbe es beim Ausprobieren anderer Indizes eine Endlosschleife). Es gilt immer <tt>self.size < self.capacity</tt>. Dies war bei der vorigen Hash-Implementation mit linearer Verkettung nicht notwendig (aber im Sinne schneller Zugriffszeiten trotzdem wünschenswert). | |||
==== Vorgehen bei Kollisionen ==== | |||
=== | =====Sequentielles Sondieren===== | ||
Probiere den nächsten Index: <tt>index = (index+1) % capacity</tt> | Probiere den nächsten Index: <tt>index = (index+1) % capacity</tt> | ||
| Line 257: | Line 214: | ||
* Nachteil: Clusterbildung | * Nachteil: Clusterbildung | ||
Clusterbildung heißt, dass sich größere zusammenhängende Bereiche bilden die belegt sind, unterbrochen von Bereichen die komplett frei sind. Beim | Clusterbildung heißt, dass sich größere zusammenhängende Bereiche bilden die belegt sind, unterbrochen von Bereichen die komplett frei sind. Beim Versuch des Einfügens eines Elements an einen Platz, der schon belegt ist, muss jetzt das ganze Cluster sequentiell durchlaufen werden, bis ein freier Platz gefunden wird. Damit entspricht die Komplexität der Suche der mittleren Länge der belegten Bereiche, was sich entsprechend in einer langsamen Suche widerspiegelt. | ||
=====Doppeltes Hashing===== | |||
[http://de.wikipedia.org/wiki/Doppel-Hashing Wikipedia (de)] [http://en.wikipedia.org/wiki/Double_hashing Wikipedia (en)] | [http://de.wikipedia.org/wiki/Doppel-Hashing Wikipedia (de)] [http://en.wikipedia.org/wiki/Double_hashing Wikipedia (en)] | ||
| Line 279: | Line 237: | ||
self.array[index] = HashNode(key, value) | self.array[index] = HashNode(key, value) | ||
self.size +=1 | self.size +=1 | ||
... # eventuell muss hier die Kapazität optimiert werden | |||
return | return | ||
if self.array[index].key == key: | if self.array[index].key == key: | ||
| Line 292: | Line 251: | ||
Die vorgestellte Implementierung orientiert sich an Pythons interner Dictionary Implementierung, der zugehörige Quelltext (mit ausführlichem Kommentar) findet sich unter [http://svn.python.org/view/*checkout*/python/trunk/Objects/dictobject.c dictobject.c Python Implementation (SVN)] | Die vorgestellte Implementierung orientiert sich an Pythons interner Dictionary Implementierung, der zugehörige Quelltext (mit ausführlichem Kommentar) findet sich unter [http://svn.python.org/view/*checkout*/python/trunk/Objects/dictobject.c dictobject.c Python Implementation (SVN)] | ||
===== Beispiel ===== | ===== Beispiel für doppeltes Hashing ===== | ||
h=25 | Der Übersichtlichkeit wegen wählen wir M'=2<sup>5</sup> (statt 2<sup>32</sup>) und eine Kapazität von M=8. | ||
Roher Hashwert (für das Beispiel willkürlich gewählt): | |||
h=25 | |||
h = h>>2 | Erster Index: | ||
i0 = h % capacity = 25 % 8 = 1 | |||
Es finde eine Kollision statt. Es wird ein zweiter Index berechnet: | |||
h = h>>2 | i1 = (5*i0 + 1 + h) % 8 = (5*1 + 1 + 25) % 8 = 31 % 8 = 7 | ||
Der Hashwert wird aktualisiert um die höherwertigen Bits von <tt>h</tt> ins Spiel zu bringen (hier durch <tt>h >> 2</tt> anstelle von <tt>h >> 5</tt> im originalen Pythoncode). Wir stellen <tt>h</tt> als Binärzahl dar, damit der Rechtsshift besser sichtbar wird: | |||
h = h >> 2 | |||
h = h>>2 | ==> h = (11001 >> 2) = 00110 = 6 | ||
Es finde wieder eine Kollision statt, so dass ein dritter Index berechnet werden muss. | |||
i2 = (5*i1 + 1 + h) % 8 = (5*7 + 1 + 6) % 8 = 42 % 8 = 2 | |||
Der Hashwert wird wiederum aktualisiert: | |||
h = h >> 2 | |||
==> h = (00110 >> 2) = 00001 = 1 | |||
Allen Indizes werden erreicht bevor sich die Folge wiederholt. | Es finde eine Kollision statt, und wir berechnen den vierten Index: | ||
i3 = (5*i2 + 1 + h) % 8 = (5*2 + 1 + 1) % 8 = 12 % 8 = 4 | |||
Der Hashwert wird nochmals aktualisiert und erreicht jetzt den Wert 0 (der sich dann nicht mehr ändert): | |||
h = h >> 2 | |||
==> h = (00110 >> 2) = 0 | |||
Es finde eine Kollision statt. Da jetzt <tt>h = 0</tt> gilt, und die Zahlen 5 (Multiplikator) und 8 (capacity) teilerfremd sind, werden ab jetzt systematisch alle Indizes von 0 bis 7 durchprobiert (in der durch die Modulo-Operation bestimmten Reihenfolge): | |||
i4 = (5*i3 + 1 + h) % 8 = (5*4 + 1 + 0) % 8 = 21 % 8 = 5 | |||
i5 = (5*i4 + 1 + h) % 8 = (5*5 + 1 + 0) % 8 = 26 % 8 = 2 | |||
i6 = (5*i5 + 1 + h) % 8 = (5*2 + 1 + 0) % 8 = 11 & 8 = 3 | |||
i7 = (5*i6 + 1 + h) % 8 = (5*3 + 1 + 0) % 8 = 16 & 8 = 0 | |||
i8 = (5*i7 + 1 + h) % 8 = (5*0 + 1 + 0) % 8 = 1 & 8 = 1 | |||
i9 = (5*i8 + 1 + h) % 8 = (5*1 + 1 + 0) % 8 = 6 & 8 = 6 | |||
i10 = (5*i9 + 1 + h) % 8 = (5*6 + 1 + 0) % 8 = 31 & 8 = 7 | |||
i11 = (5*i10 + 1 + h) % 8 = (5*7 + 1 + 0) % 8 = 36 & 8 = 4 | |||
Allen Indizes werden also erreicht, bevor sich die Folge wiederholt. Da man <tt>capacity</tt> immer so wählt, dass mindestens ein Arrayfeld noch frei ist, wird dadurch immer ein geeigneter Platz für das einzufügende Element gefunden. | |||
==== Komplexität der offenen Adressierung ==== | |||
* Annahme: uniformes Hashing, das heißt alle Indizes haben gleiche Wahrscheinlichkeit | * Annahme: uniformes Hashing, das heißt alle Indizes haben gleiche Wahrscheinlichkeit | ||
* Füllstand <math>\alpha = \frac{\text{size}}{\text{capacity}}</math> | * Füllstand <math>\alpha =\frac{N}{M} = \frac{\text{size}}{\text{capacity}}</math> | ||
* '''Erfolglose Suche''' (d.h. es wird entweder ein neues Element eingefügt oder ein <tt>KeyError</tt> geworfen): Untere Schranke für die Komplexität ist <math>\Omega\left(\frac{1}{1-\alpha}\right)</math> Schritte (= Anzahl der notwendigen index-Berechnungen). | * '''Erfolglose Suche''' (d.h. es wird entweder ein neues Element eingefügt oder ein <tt>KeyError</tt> geworfen): Untere Schranke für die Komplexität ist <math>\Omega\left(\frac{1}{1-\alpha}\right)</math> Schritte (= Anzahl der notwendigen index-Berechnungen). | ||
* '''Erfolgreiche Suche''' <math>\Omega\left(\frac{1}{\alpha}\ln\left(\frac{1}{1-\alpha}\right)\right)</math> Schritte. | * '''Erfolgreiche Suche''' <math>\Omega\left(\frac{1}{\alpha}\ln\left(\frac{1} {1-\alpha}\right)\right)</math> Schritte. | ||
{| border="1" cellspacing="0" cellpadding="5" align="center" | {| border="1" cellspacing="0" cellpadding="5" align="center" | ||
| Line 334: | Line 307: | ||
|} | |} | ||
==== Wahl der Kapazität ==== | |||
In Python wird <tt>capacity</tt> | Man sieht an der obigen Tabelle, dass die erfolglose Suche (und damit das Einfügen) sehr langsam wird, wenn der Füllstand hoch ist. In Python wird <tt>capacity</tt> deshalb so gewählt, dass <math>\alpha \leq 2/3</math>. Falls <math>\alpha</math> größer werden sollte, verdopple die Kapazität und kopiere das alte array in das neue Array (analog zum dynamischen Array) | ||
In Python werden die Kapazitätsgrößen als Zweierpotenzen gewählt, also 4,8,16,32,..., | In Python werden die Kapazitätsgrößen als Zweierpotenzen gewählt, also 4,8,16,32,..., | ||
so dass <tt>h % self.capacity</tt> nur die unteren Bits von <tt>h</tt> benutzt. | so dass <tt>h % self.capacity</tt> nur die unteren Bits von <tt>h</tt> benutzt. Die oberen Bits von <tt>h</tt> kommen erst ins Spiel, wenn bei der Berechnung der 2. Hashfunktion die Aktualisierung <tt>h = h >> 5</tt> erfolgt. Dies hat sich bei umfangreichen Experimenten als sehr gute Lösung erwiesen. | ||
== Anwendung von Hashing == | == Anwendung von Hashing == | ||
| Line 352: | Line 325: | ||
In Textverarbeitungsanwendungen ist eine häufig benutzte Funktion die ''Search & Replace'' Funktionalität. Die Suche sollte in O(len(text)) möglich sein, aber ein naiver Algorithmus braucht O(len(text)*len(searchstring)) | In Textverarbeitungsanwendungen ist eine häufig benutzte Funktion die ''Search & Replace'' Funktionalität. Die Suche sollte in O(len(text)) möglich sein, aber ein naiver Algorithmus braucht O(len(text)*len(searchstring)) | ||
==== Naive Implementierung der | ==== Naive Implementierung der Textsuche ==== | ||
def search(text, s): | def search(text, s): | ||
M, N = len(text), len(s) | M, N = len(text), len(s) | ||
| Line 369: | Line 342: | ||
Idee: Interpretiere den Text als Ziffern in einer base d Darstellung: | Idee: Interpretiere den Text als Ziffern in einer base d Darstellung: | ||
<math>h_k = \text{text}[k]\cdot d^{N-1} + \text{text}[k]\cdot d^{N-2} + \cdots + \text{text}[k+N-1]</math> | <math>h_k = \text{text}[k]\cdot d^{N-1} + \text{text}[k+1]\cdot d^{N-2} + \cdots + \text{text}[k+N-1]</math> | ||
Für die Basis 10 (Dezimalsystem) ergibt sich also | Für die Basis 10 (Dezimalsystem) ergibt sich also | ||
<math>h_k = \text{text}[k]\cdot {10}^{N-1} + \text{text}[k]\cdot {10}^{N-2} + \cdots + \text{text}[k+N-1]</math> | <math>h_k = \text{text}[k]\cdot {10}^{N-1} + \text{text}[k+1]\cdot {10}^{N-2} + \cdots + \text{text}[k+N-1]</math> | ||
Daraus folgt | Daraus folgt | ||
<math>h_{k+1} = 10\cdot h_k - \text{text}[k]\cdot {10}^{N} + \text{text}[k+N]</math> | <math>h_{k+1} = 10 \cdot h_k - \text {text}[k]\cdot {10}^{N} + \text {text}[k+N]</math> | ||
Die Komplexität dieses Updates ist O(1), falls man <math>{10}^{N}</math> vorberechnet hat. | Die Komplexität dieses Updates ist O(1), falls man <math>{10}^{N}</math> vorberechnet hat. | ||
In der Realität wählt man dann d=32 und benutzt noch an einigen Stellen modulo Operationen, um die Zahlen nicht zu groß werden zu lassen. | In der Realität wählt man dann d=32 und benutzt noch an einigen Stellen modulo Operationen, um die Zahlen nicht zu groß werden zu lassen (siehe die Zahl <tt>q</tt> in der folgenden Implementation). | ||
==== Implementation ==== | ==== Implementation ==== | ||
def searchRabinKarp(text, s): | def searchRabinKarp(text, s): | ||
M, N = len(text), len(s) | M, N = len(text), len(s) | ||
d | d = 32 | ||
#q ist eine große Primzahl, aber so, | q = 33554393 # q ist eine große Primzahl, aber so, | ||
# dass d*q < 2**32 (um Überlauf bei 32-bit Integerarithmetik zu vermeiden) | |||
dN = d**N % q # Vorberechnung des Vorfaktors für das Entfernen aus dem Hash | |||
#Initialisierung | # Initialisierung | ||
hs, ht = 0, 0 | |||
for k in range(N): | for k in range(N): | ||
# ord() gibt die Zeichen-Nummer (z.B. ASCII- oder UTF-8-Code) des | |||
# übergebenen Zeichens zurück | |||
hs = (hs*d + ord( s[k] )) % q | |||
ht = (ht*d + ord(text[k])) % q | ht = (ht*d + ord(text[k])) % q | ||
# Die Variablen sind jetzt wie folgt initialisiert: | |||
# hs = hash(s) | |||
# ht = hash(text[0:N]) | |||
#Die Variablen sind jetzt wie folgt initialisiert: | |||
#hs = hash(s) | |||
# | |||
#Hauptschleife | # Hauptschleife | ||
k = 0 | k = 0 | ||
while k < M-N: | while k < M-N: | ||
if hs == ht | if hs == ht: # übereinstimmende Hashs => prüfe, dass es nicht nur | ||
# eine Kollision ist | |||
if s == text[k:k+N]: # O(N)-Vergleich nur nötig, wenn Hashs übereinstimmen | |||
return k # search string an Position k gefunden | |||
# nicht gefunden => aktualisiere Hash für den nächsten Teilabschnitt von text: | |||
ht = (d*ht + ord(text[k+N])) % q # neues Zeichen text[k+N] in Hash einfügen | |||
ht = (ht - dN*ord(text[k])) % q # Zeichen text[k] aus Hash entfernen. | |||
k +=1 | k +=1 | ||
return -1 # search string nicht gefunden | return -1 # search string nicht gefunden | ||
[[Iteration versus Rekursion|Nächstes Thema]] | |||
Latest revision as of 16:25, 13 June 2012
Die Mitschrift gibts auch als PDF.
Assoziative Arrays
Assoziative Arrays werden genau wie gewöhnliche Arrays benutzt, sie unterstützen also den lesenden und schreibenden Zugriff über einen Index i
X = a[i] a[i] = x
Im Unterschied zum gewöhnlichen Array, wo i ein Integer im Bereich <math> i \in 0 \ldots N-1</math> sein muss, kann der Typ von i jetzt beliebig sein. Eine typische Anwendung ist ein Wörterbuch
x = toEnglish['Baum'] # ergibt 'tree'
In diesem Fall ist der Typ des Index string, was in der Praxis der häufigste Fall ist, weshalb assoziative Arrays oft als Dictionary bezeichnet werden (so auch in Python, hier heißt der Typ dict). Im allgemeinen kann aber jeder Typ als Index benutzt werden, für den entweder eine Ordnung oder eine Hashfunktion definiert ist. Im ersten Fall realisiert man das assoziative Array mit Hilfe eines Suchbaums, im zweiten Fall mit Hilfe einer Hashtabelle.
Realisierung des assoziativen Arrays als Suchbaum
Wenn für den Indextyp des assoziativen Arrays eine Ordnung definiert ist (wenn also i1 < i2 oder cmp(i1, i2) unterstützt werden), kann man das Indexierungsproblem auf das Suchproblem zurückführen, indem man die Indizes als Suchschlüssel verwendet. Im einfachsten Fall kann dies mit sequentieller Suche realisiert werden: Man verwendet ein gewöhnliches Array, dessen Einträge (Schlüssel, Daten)-Paare sind. Bei der Frage nach einem Schlüssel wird das betreffende Paar gesucht und die darin gespeicherten Daten zurückgegeben. Dies erfordert aber einen Suchaufwand in O(n). Effizienter geht es mit einem Suchbaum. Die Datenstruktur des Suchbaums muss dafür so erweitert werden, dass zu jedem Schlüssel (=Index) weitere Informationen gespeichert werden können (nämlich der Inhalt des indexierten Feldes). Man erweitert die Node-Klasse um ein Feld "data":
class Node:
def __init__(self, key, data = None):
self.key = key
self.data = data
self.left = self.right = None
Dann kann man eine Klasse AssociativeArray realisieren, die die Indexoperationen intern mit Hilfe der Baumsuche implementiert. In Python wird der Zugriffsoperator [ ] für eine Datenstruktur (also innerhalb einer Klasse) wie folgt implementiert (vgl. die Python Docs zum Thema):
def __setitem__(self, key, value)
so dass im Programmtext dann folgende Syntax möglich ist: a[key] = value (schreibender Zugriff auf a[key]). Analog wird der lesende Zugriff value = a[key] wie folgt umgesetzt:
def __getitem__(self, key, value)
Der Konstruktor der Klasse AssociativeArray initialisiert einen leeren Suchbaum:
class AssociativeArray:
def __init__(self):
self.root = None
self.size = 0
Die Funktion __setitem__ schaut nach, ob ein Eintrag mit dem betreffenden Index bereits existiert. Wenn ja, werden seine Daten mit den neuen Daten überschrieben, andernfalls wird ein neuer Eintrag angelegt. Intern werden dazu die bereits bekannten Funktionen treeSearch und treeInsert verwendet (siehe Abschnitt Suchbäume):
def __setitem__(self, index, data):
node = treeSearch(self.root, index)
if node is None:
self.root = treeInsert(self.root, index)
self.size += 1
node = treeSearch(self.root, index)
node.data = data
(Eine geschicktere Implementation würde natürlich die wiederholten Aufrufe von treeSearch und treeInsert eliminieren. Dies ändert aber nichts an der Komplexität der Funktion.) Die Funktion __getitem__ sucht ebenfalls einen Eintrag mit dem gegebenen Index. Wenn er gefunden wird, gibt sie die zugehörigen Daten zurück, andernfalls eine Fehlermeldung:
def __getitem__(self, index):
node = treeSearch(self.root, index)
if node is None:
raise KeyError(index)
else:
return node.data
Die Indexoperationen haben bei der Realisierung mit Baumsuche eine Komplexität in O(log n).
Ein wichtiges Beispiel für ein assoziatives Array, das auf diese Weise realisiert wurde, ist die C++ Standardklasse std::map.
Hashing
Nun stellt sich die Frage, ob die Suche in einem assoziativen Array auch schneller, möglicherweise sogar in O(1), geht. Die Antwort lautet: Ja, wenn für die Indexklasse eine Hashfunktion definiert ist.
Hashfunktionen
Gegeben sei ein Universum U, dass die Menge aller legalen Schlüssel darstellt. Die Mächtigkeit |U| der Menge U ist im allgemeinen sehr groß. Beispielsweise kann man mit Strings der Länge 9 bis zu 279≈1013≈243 verschiedene Schlüssel generieren, wenn 27 Zeichen erlaubt sind (Kleinbuchstaben und Leerzeichen). Die Grundannahme von Hashing ist jetzt, dass in jeder gegebenen Anwendung nur ein (kleiner) Teil der erlaubten Schlüssel tatsächlich verwendet wird. Man definiert eine Hashfunktion, die jeden Schlüssel auf eine natürliche Zahl im Bereich 0...(M-1) abbildet, wobei M viel kleiner als |U| ist.
- Definition einer Hashfunktion
-
- <math> f: U \rightarrow [0, 1, \ldots, M-1] \subset \mathbb{N} </math>
- <math> f(u \in U) = h \in [0, 1, \ldots, M-1]</math>
h wird als Hashwert von u bezeichnet. Da M < |U|, werden notwendigerweise einige Schlüssel auf dieselbe Zahl abgebildet. Man bezeichnet den Fall <math> f(u_1 \in U) = f(u_2 \in U) </math> als Kollision zwischen den Schlüsseln u1 und u2.
Die Aufgabe besteht jetzt darin, ein Hash-Funktion zu entwerfen, die möglichst wenige Kollisionen hat. Hashfunktionen ähneln damit einem Zufallszahlengenerator, weil jede Zahl <math> h \in 0 \ldots (M-1) </math> nach Möglichkeit mit gleicher Wahrscheinlichkeit herauskommen soll. Wird dieses Ziel erreicht, spricht man vom uniformen Hashing.
In der Regel ist aber nicht vorher bekannt, welche Schlüssel in einer Anwendung verwendet werden. Es kann deshalb immer vorkommen, dass die verwendete Schlüsselmenge sehr viele Kollisionen verursacht. Man sieht in der Tat leicht ein, dass für jede gegebene Hashfunktion ungünstige Schlüsselmengen <math> U_f \subset U</math> existieren, bei denen es sehr viele Kollisionen gibt. Im ungünstigsten Fall könnte Uf so gewählt sein, dass f(Uf) = k = const. gilt. Ein Hacker, der die verwendete Hashfunktion kennt, kann z.B. Uf absichtlich so wählen, um eine denial-of-service-Attacke gegen einen hash-basierten Webservice zu starten. Ein anderes anschauliches Beispiel wäre eine Party, zu der nur Leute eingeladen werden, die an einem 8ten im Monat Geburtstag haben. Auf dieser Party ist es viel wahrscheinlicher, Leute zu finden, die am selben (oder gleichen) Tag Geburtstag haben, als wenn man alle einlädt.
D.h. die Wahl einer guten Hashfunktion ist eine Kunst, und man muss (wenn möglich) die Daten analysieren um ein gutes f zu finden.
Perfektes Hashing
Kennt man die Untermenge der tatsächlich vorkommenden Schlüssel <math>U_f \subset U</math> schon im voraus, hat man die Möglichkeit, eine perfekte Hashfunktion ohne Kollisionen zu entwerfen.
- Beispiel anhand der Monatsnamen
U ist in diesem Fall eine Menge von Strings der Länge 9 (weil der September als längster Monatsname 9 Zeichen hat). Es ergeben sich also <math>60^{9}</math>>≈1016≈254 mögliche Strings, da mit Groß- und Kleinbuchstaben, Umlauten, ß und Leerzeichen 60 Zeichen im deutschen Alphabet vorhanden sind. Von all diesen Möglichkeiten werden genau 12 benutzt:
- <math>U_f</math> = {"Januar"; "Februar"; ... ; "Dezember"}
- Benutzt man nun als Hashfunktion die Anfangsbuchstaben der Monatsnamen, benötigt man dafür 6 bit. M ist somit 64.
- {"Januar"; "Februar"; ... ; "Dezember"} → {"J"; "F"; "M"; "A"; "M"; "J"; "J"; "A"; "S"; "O"; "N"; "D"}
- Dabei enstehen viele Kollisionen (J wird 3x verwendet, M 2x, A 2x), die gewählte ist also keine gute Hashfunktion
- Benutzt man als Hashfunktion die ersten 3 Buchstaben benötigt man 18 bit, M = <math>2^{18}</math>
- {"Januar"; "Februar"; ... ; "Dezember"} → {"Jan", "Feb", "März", "Apr", "Mai", "Jun", "Jul", "Aug", "Sep", "Okt", "Nov", "Dez"}
- Nun entstehen keine Kollision mehr. Diese Hashfunktion ist deshalb beim Ausfüllen von Formularen und dergleichen sehr beliebt. Dafür ist M aber recht groß.
Die Aufgabe wird also präzisiert: man sucht für <math>U_f</math> eine minimale, perfekte Hashfunktion, für die <math>|U_f| = M</math> gilt. Ein Verfahren hierfür ist Gegenstand von Übungsblatt 9.
Universelles Hashing
Hier wählt man für eine gegebene Hashtabelle die Hashfunktion per Zufallszahl aus einer (großen) Menge erlaubter Hashfunktion → Die Wahrscheinlichkeit, dass die Hashfunktion für die Schlüssel ungünstig ist, wird dadruch minimiert. Die oben erwähnte denial-of-service-Attacke ist jetzt nicht mehr möglich, weil kein Hacker die Hashfunktion im voraus kennen kann. Näheres zum universellen Hashing finden Sie in der Wikpedia.
Kryptographische Hashfunktionen
In kryptographischen Anwendungen treten neben dem Hauptziel, die Größe des Universums auf eine überschaubare Zahl von Integer-Werten zu reduzieren, zwei weitere Anforderungen, die für Verschlüsselung bzw. verschlüsselte Kommunikation wichtig sind: erstens will man Kollisionen unbedingt vermeiden (damit zwei verschiedene Dokumente oder Passwörter nicht auf den gleichen Hashwert abgebildet werden), und zweitens darf es nicht möglich sein, aus dem Hashwert die urpsrüngliche Nachricht (also das Dokument oder Passwort) zu rekonstruieren. Man wählt deshalb relative große M (128 bit und mehr) sowie spezielle, für diesen Zweck optimierte Hashfunktionen, wie z.B. md5 und sha1. Weitere Einzelheiten finden Sie in der Wikipedia.
Beliebte Standard-Hashfunktionen
In der Praxis definiert man Hashfunktionen gewöhnlich zweistufig: Zunächst bildet man den Schlüssel auf einen 32 bit Integerwert ab, M' ist damit 232. Dieser "rohe" Hashwert wird dann mittels der Modulo-Operation auf die eigentliche Größe M des assoziativen Arrays abgebildet:
- <math> f(u \in U) = f'(u \in U)\,\%\,M\,=\,h \in [0, 1, \ldots, M-1] </math>
mit
- <math> f'(u \in U) = h' \in [0, 1, \ldots, 2^{32}-1] </math>
Der große Wert von M' sichert, dass man bei der Wahl von M großen Spielraum hat, so dass die Größe des assoziativen Arrays sehr gut an die Menge der zu speichernden Daten angepaßt werden kann. Die Funktion f'(u) definiert man wie folgt:
- Falls U = unsigned int (32bit int Datentyp) ⇒ f'(u) = u
- Falls U = signed int ⇒ Typkonvertierung nach unsigned int ⇒ f'(u) = (unsigned int)u
- Andere Schlüsseltypen (also insbesondere Strings) interpretiert man als Array of byte ⇒ f'(u) konvertiert Array of Byte nach unsigned int. Beispiele für solche Funktionen:
- Bernsteinfunktion:
def bHash(u): # u: Array of Byte
h=0
for k in u:
h = 33 * h + k
return h
- modifizierte Bernsteinfunktion:
def mbHash(u): # u: Array of Byte
h=0
for k in u:
h = (33 * h) ^ k # ^ ist bitweises Xor
return h
- Shift-Add-Xor-Funktion:
def saxhash(u): # u: Array of Byte
h=0
for k in u:
h ^= (h << 5) + (h >> 2) + k # << und >> sind Links- bzw. Rechtsshift der Bits, ^= ist bitweise Xor-Zuweisung
return h
- Fowler/Noll/Vo-Funktion:
def FNVhash(u): # u: Array of Byte
h = 2166136261
for k in u:
h = (16777619 * h) ^ k # ähnlich der modifizierten Bernsteinfunktion, aber mit anderen Konstanten
return h
- Die verwendeten Konstanten sind experimentell so gewählt worden, dass die Hashfunktionen in typischen Praxisanwendungen relativ wenige Kollisionen verursachen. Der tiefere Grund, warum z.B. 33 in der Bernsteinfunktion eine gute Wahl darstellt, ist unbekannt. Es empfielt sich, in einer gegebenen Anwendung mit mehreren Hashfunktionen zu experimentieren. Weitere solche Funktionen und andere nützliche Informationen findet man auf der Seite eternallyconfuzzled.com.
Hashtabellen
Eine Hashtabelle ist eine Datenstruktur, die die Funktionalität des assoziativen Arrays mit Hilfe von Hashing realisiert. Das Grundprinzip besteht darin, dass die Hashtabelle intern ein (dynamisches) Array der Größe capacity verwaltet, so dass die Hashwerte als Indizes in diesem Array verwendet werden können (capacity entspricht der Zahl M aus der mathematischen Definition oben). Eine naive Implementation der Einfügeoperation sieht also so aus
def __setitem__(self, key, value): # naive Implementation, funktioniert so nicht
index = self.hash(key) % self.capacity
self.array[index] = value
Diese Implementation ist allerdings zu einfach. Wenn nämlich die Schlüssel aus dem Universum U beliebig gewählt werden dürfen, sind Kollisionen unvermeidlich. Tritt aber eine Kollision auf, werden die Daten eines Schlüssels mit den Daten eines anderen Schlüssels überschrieben. Um Kollisionen geschickt zu behandeln gibt es zwei Ansätze:
- lineare Verkettung
- offene Adressierung
Hashtabelle mit linearer Verkettung (offenes Hashing/geschlossene Adressierung)
Man kann dies als die pessimistische Lösung bezeichnen: Man nimmt an, dass Kollisionen häufig auftreten. Deshalb wird unter jedem Hashindex gleich eine Liste angelegt, in der Einträge mit gleichem Hashindex aufgenommen werden können. Die Hashtabelle verwaltet ein Array von Listen, und jedes Arrayfeld kann beliebig viele Elemente speichern: Wird ein Element auf den Index i abgebildet, werden die Daten einfach an die betreffende Liste angehängt. Bei Zugriff auf ein Element wird zunächst die passende Liste gesucht (mit Hilfe des Hashwerts), danach erfolgt in dieser Liste eine sequentielle Suche nach dem richtigen Schlüssel.
Um diese Idee implementieren zu können, benötigen wir zunächst eine Hilfsklasse HashNode, die (Schlüssel, Wert)-Paare speichert und mit Hilfe von next eine verkettete Liste realisiert:
class HashNode:
def __init__(self,key,data,next):
self.key = key
self.data = data
self.next = next # Verkettung!
Die eigentliche Hashtabelle wird in der Klasse HashTable implementiert:
class HashTable:
def __init__(self):
self.capacity = ... # Geeignete Werte siehe unten
self.size = 0 # Anzahl der Werte, die zur Zeit tatsächlich gespeichert sind
self.array = [None]*self.capacity
Wie oben bereits erwähnt, werden die Zugriffsoperatoren [ ] für eine Datenstruktur in Python durch die Funktionen __setitem__ bzw. __getitem__ implementiert. Die __setitem__-Funktion speichert die gegebenen Daten unter dem Schlüssel key in der HashTable-Klasse:
def __setitem__(self, key, value):
index = hash(key) % self.capacity # hash(...) ist in Python eine vordefinierte Funktion
node = self.array[index] # finde die zu 'key' gehörende Liste
while node is not None: # sequentielle Suche nach 'key' in dieser Liste
if node.key == key:
# Element 'key' ist schon in der Tabelle
# => überschreibe die Daten mit dem neuen Wert
node.data = value
return
# andernfalls: Kollision des Hashwerts, probiere nächsten 'key' aus
node = node.next
# kein Element hatte den richtigen Schlüssel.
# => es gibt diesen Schlüssel noch nicht
# füge also ein neues Element in die Hashtabelle ein
self.array[index] = HashNode(key, value, self.array[index]) # der alte Anfang der Liste wird zum
# Nachfolger des neu eingefügten ersten Elements
self.size += 1
... # eventuell muss jetzt noch die Kapazität optimiert werden
Die Funktion __getitem__ gibt die unter dem Schlüssel key abgelegten Daten zurück, oder eine Fehlermeldung, falls dieser Schlüssel nicht existiert:
def __getitem__(self, key):
index = hash(key) % self.capacity
node = self.array[index] # finde die zu 'key' gehörende Liste
while node is not None: # sequentielle Suche nach 'key' in dieser Liste
if node.key == key: # gefunden!
return node.data # => Daten zurückgeben
node = node.next # nächsten Schlüssel probieren
raise KeyError(key) # Schlüssel nicht gefunden => Fehler
Komplexität der linearen Verkettung und Wahl der Kapazität
Die Komplexität wird durch zwei Operationen bestimmt: erstens das Auffinden der zu einem Schlüssel gehörenden Liste (die in O(1) erfolgt), zweitens das sequentielle Durchsuchen der Liste, die Zeit in O(L) erfordert, wobei L die mittlere Länge der Listen ist. Die Hashtabelle ist also nur schnell, wenn die Länge der Listen möglichst klein ist. Unter der Annahme des uniformen Hashings, wenn also alle Indizes gleich häufig verwendet werden, ist L gleich dem Füllstand der Hashtabelle:
- <math>\alpha = \frac{N}{M} = \frac{\text{size}}{\text{capacity}}</math> wobei N die Größe size der Hashtabelle und M die Größe capacity des Arrays ist.
Wenn die Hashwerte uniform sind, entfallen auf jede Liste im Mittel N/M Einträge (N Einträge, verteilt auf M Listen). Die Gesamtkomplexität berechnet sich nach der Sequenzregel zu
- <math>O(1+\alpha)</math>
Für eine effiziente Suche muss demnach <math>\alpha \in O(1)</math> gewählt werden. Dies erreicht man, indem man, wie beim dynamischen Array, capacity immer wieder anpasst, falls size zu groß wird. Üblicherweise verdoppelt man capacity, sobald size == capacity erreicht wird. Analog zum dynamischen Array werden die Daten dann aus dem alten Array (self.array) in ein entsprechend vergrößertes neues Array kopiert.
In der C++ Standardbibliothek (Klasse std::unordered_map, siehe auch GCC hashtable_aux.cc (Primzahlen) und GCC Hash Implementation) wird die Hashtabelle häufig so implementiert. Dabei wird capacity immer als Primzahl gewählt, wobei sich aufeinanderfolgende Kapazitäten immer ungefähr verdoppeln. Dazu wählt man aus einer vorberechneten Liste von Primzahlen die kleinste Zahl, so dass new_capacity >= 2*capacity gilt, und beginnt z.B. mit einer Default-Kapazität von 11:
11, 23, 47, 97, 199, 409, 823, ...
Die Wahl von Primzahlen hat zur Folge, dass hash(key) % self.capacity alle Bits von h benutzt (Eigenschaft aus der Zahlentheorie). Die Kapazität wird vergrößert, wenn size == capacity erreicht wird, und die ungefähre Verdoppelung sichert, dass die amortisierte Komplexität der Einfügeoperation in O(1) ist (wie beim dynamischen Array).
Hashtabelle mit offener Adressierung (geschlossenes Hashing)
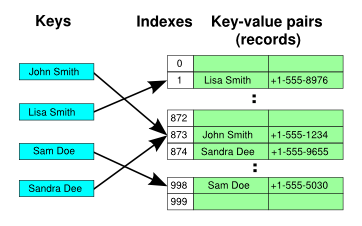
Dies kann als die optimistische Variante betrachtet werden: man nimmt an, dass Kollisionen nicht so häufig auftreten, um eine komplexe Datenstruktur wie das "Array von Listen" zu rechtfertigen. Stattdessen behandelt man Kollisionen mit einer einfachen Idee: Wenn array[index] durch Kollision bereits vergeben ist, probiere einen anderen Index aus (siehe auch Wikipedia (de) und Wikipedia (en)). Dabei muss man folgendes beachten:
- Das Array enthält pro Element höchstens ein (key,value)-Paar
- Das Array muss stets mindestens einen freien Platz haben (sonst gäbe es beim Ausprobieren anderer Indizes eine Endlosschleife). Es gilt immer self.size < self.capacity. Dies war bei der vorigen Hash-Implementation mit linearer Verkettung nicht notwendig (aber im Sinne schneller Zugriffszeiten trotzdem wünschenswert).
Vorgehen bei Kollisionen
Sequentielles Sondieren
Probiere den nächsten Index: index = (index+1) % capacity
- Vorteil: einfach
- Nachteil: Clusterbildung
Clusterbildung heißt, dass sich größere zusammenhängende Bereiche bilden die belegt sind, unterbrochen von Bereichen die komplett frei sind. Beim Versuch des Einfügens eines Elements an einen Platz, der schon belegt ist, muss jetzt das ganze Cluster sequentiell durchlaufen werden, bis ein freier Platz gefunden wird. Damit entspricht die Komplexität der Suche der mittleren Länge der belegten Bereiche, was sich entsprechend in einer langsamen Suche widerspiegelt.
Doppeltes Hashing
Bestimme einen neuen Index (bei Kollisionen) durch eine 2. Hashfunktion.
Das doppelte Hashing wird typischerweise in der Praxis angewendet und liegt auch der Python Implementierung des Datentyps Dictionary (Syntax {'a':1, 'b':2, 'c':3} zugrunde.
Eine effiziente Implementierung dieses Datentyps ist für die Performance der Skriptsprache Python extrem wichtig, da z.B. beim Aufruf einer Funktion der auszuführunde Code in einem Dictionary unter dem Schlüssel Funktionsname nachgeschlagen wird oder die Werte lokaler Variablen innerhalb einer Funktion ebenfalls in einem Dictionary zu finden sind.
Für die Implementierung in Python werden wieder die obigen Klassen HashNode (das Attribut next kann allerdings jetzt entfernt werden) und HashTable benötigt, es folgen die angepassten Implementationen von __setitem__ und __getitem__:
def __setitem__(self, key, value):
h = hash(key)
index = h % self.capacity
while True:
if self.array[index] is None or self.array[index].key is None:
# das Feld ist frei (1. Abfrage)
# oder das Feld ist als frei markiert (2. Abfrage)
self.array[index] = HashNode(key, value)
self.size +=1
... # eventuell muss hier die Kapazität optimiert werden
return
if self.array[index].key == key:
# Es gibt diesen Schlüssel schon,
# überschreibe die Daten
self.array[index].data = value
return
# Letzter Fall: Kollision => neuer Index durch 2. Hashfunktion
index = (5*index+1+h) % self.capacity
h = h >> 5
(für den >>-Operator, siehe die Python Dokumentation)
Die vorgestellte Implementierung orientiert sich an Pythons interner Dictionary Implementierung, der zugehörige Quelltext (mit ausführlichem Kommentar) findet sich unter dictobject.c Python Implementation (SVN)
Beispiel für doppeltes Hashing
Der Übersichtlichkeit wegen wählen wir M'=25 (statt 232) und eine Kapazität von M=8.
Roher Hashwert (für das Beispiel willkürlich gewählt):
h=25
Erster Index:
i0 = h % capacity = 25 % 8 = 1
Es finde eine Kollision statt. Es wird ein zweiter Index berechnet:
i1 = (5*i0 + 1 + h) % 8 = (5*1 + 1 + 25) % 8 = 31 % 8 = 7
Der Hashwert wird aktualisiert um die höherwertigen Bits von h ins Spiel zu bringen (hier durch h >> 2 anstelle von h >> 5 im originalen Pythoncode). Wir stellen h als Binärzahl dar, damit der Rechtsshift besser sichtbar wird:
h = h >> 2 ==> h = (11001 >> 2) = 00110 = 6
Es finde wieder eine Kollision statt, so dass ein dritter Index berechnet werden muss.
i2 = (5*i1 + 1 + h) % 8 = (5*7 + 1 + 6) % 8 = 42 % 8 = 2
Der Hashwert wird wiederum aktualisiert:
h = h >> 2 ==> h = (00110 >> 2) = 00001 = 1
Es finde eine Kollision statt, und wir berechnen den vierten Index:
i3 = (5*i2 + 1 + h) % 8 = (5*2 + 1 + 1) % 8 = 12 % 8 = 4
Der Hashwert wird nochmals aktualisiert und erreicht jetzt den Wert 0 (der sich dann nicht mehr ändert):
h = h >> 2 ==> h = (00110 >> 2) = 0
Es finde eine Kollision statt. Da jetzt h = 0 gilt, und die Zahlen 5 (Multiplikator) und 8 (capacity) teilerfremd sind, werden ab jetzt systematisch alle Indizes von 0 bis 7 durchprobiert (in der durch die Modulo-Operation bestimmten Reihenfolge):
i4 = (5*i3 + 1 + h) % 8 = (5*4 + 1 + 0) % 8 = 21 % 8 = 5 i5 = (5*i4 + 1 + h) % 8 = (5*5 + 1 + 0) % 8 = 26 % 8 = 2 i6 = (5*i5 + 1 + h) % 8 = (5*2 + 1 + 0) % 8 = 11 & 8 = 3 i7 = (5*i6 + 1 + h) % 8 = (5*3 + 1 + 0) % 8 = 16 & 8 = 0 i8 = (5*i7 + 1 + h) % 8 = (5*0 + 1 + 0) % 8 = 1 & 8 = 1 i9 = (5*i8 + 1 + h) % 8 = (5*1 + 1 + 0) % 8 = 6 & 8 = 6 i10 = (5*i9 + 1 + h) % 8 = (5*6 + 1 + 0) % 8 = 31 & 8 = 7 i11 = (5*i10 + 1 + h) % 8 = (5*7 + 1 + 0) % 8 = 36 & 8 = 4
Allen Indizes werden also erreicht, bevor sich die Folge wiederholt. Da man capacity immer so wählt, dass mindestens ein Arrayfeld noch frei ist, wird dadurch immer ein geeigneter Platz für das einzufügende Element gefunden.
Komplexität der offenen Adressierung
- Annahme: uniformes Hashing, das heißt alle Indizes haben gleiche Wahrscheinlichkeit
- Füllstand <math>\alpha =\frac{N}{M} = \frac{\text{size}}{\text{capacity}}</math>
- Erfolglose Suche (d.h. es wird entweder ein neues Element eingefügt oder ein KeyError geworfen): Untere Schranke für die Komplexität ist <math>\Omega\left(\frac{1}{1-\alpha}\right)</math> Schritte (= Anzahl der notwendigen index-Berechnungen).
- Erfolgreiche Suche <math>\Omega\left(\frac{1}{\alpha}\ln\left(\frac{1} {1-\alpha}\right)\right)</math> Schritte.
| <math>\alpha</math> | 0.5 | 0.9 |
|---|---|---|
| erfolglos | 2.0 | 10 |
| erfolgreich | 1.4 | 2.6 |
Wahl der Kapazität
Man sieht an der obigen Tabelle, dass die erfolglose Suche (und damit das Einfügen) sehr langsam wird, wenn der Füllstand hoch ist. In Python wird capacity deshalb so gewählt, dass <math>\alpha \leq 2/3</math>. Falls <math>\alpha</math> größer werden sollte, verdopple die Kapazität und kopiere das alte array in das neue Array (analog zum dynamischen Array)
In Python werden die Kapazitätsgrößen als Zweierpotenzen gewählt, also 4,8,16,32,..., so dass h % self.capacity nur die unteren Bits von h benutzt. Die oberen Bits von h kommen erst ins Spiel, wenn bei der Berechnung der 2. Hashfunktion die Aktualisierung h = h >> 5 erfolgt. Dies hat sich bei umfangreichen Experimenten als sehr gute Lösung erwiesen.
Anwendung von Hashing
- Hashtabelle, assoziatives Aray
- Sortieren in linearer Zeit (Übungsaufgabe 6.2)
- Suchen von Strings in Texten: Rabin-Karp-Algorithmus
- ...
Rabin Karp Algorithmus
In Textverarbeitungsanwendungen ist eine häufig benutzte Funktion die Search & Replace Funktionalität. Die Suche sollte in O(len(text)) möglich sein, aber ein naiver Algorithmus braucht O(len(text)*len(searchstring))
Naive Implementierung der Textsuche
def search(text, s):
M, N = len(text), len(s)
for k in range(M-N):
if s==text[k:k+N]: # O(N), da N Zeichen verglichen werden müssen
return k
return -1 #nicht gefunden
Idee des Rabin Karp Algorithmus
Statt Vergleichen s==text[k:k+N], die O(N) benötigen da N Vergleiche der Buchstaben durchgeführt werden müssen, Vergleiche die Hashs von Suchstring und dem zu untersuchenden Textabschnitt: hash(s) == hash(text[k:k+N]). Dabei muss natürlich hash(s) nur einmal berechnet werden, wohingegen hash(text[k:k+N]) immer wieder neu berechnet werden muss. Damit der Vergleich O(1) sein kann, ist es deswegen erforderlich, eine solche Hashfunktion zu haben, die nicht alle Zeichen (das wäre O(N) ) einlesen muss, sondern die vorhergehende Hashfunktion mit einbezieht.
Eine solche Hashfunktion heißt Running Hash und funktioniert analog zum Sliding Mean.
Die Running Hash Funktion berechnet in O(1) den hash von text[k+1:k+1+N] ausgehend vom hash für text[k:k+N].
Idee: Interpretiere den Text als Ziffern in einer base d Darstellung:
<math>h_k = \text{text}[k]\cdot d^{N-1} + \text{text}[k+1]\cdot d^{N-2} + \cdots + \text{text}[k+N-1]</math>
Für die Basis 10 (Dezimalsystem) ergibt sich also
<math>h_k = \text{text}[k]\cdot {10}^{N-1} + \text{text}[k+1]\cdot {10}^{N-2} + \cdots + \text{text}[k+N-1]</math>
Daraus folgt
<math>h_{k+1} = 10 \cdot h_k - \text {text}[k]\cdot {10}^{N} + \text {text}[k+N]</math>
Die Komplexität dieses Updates ist O(1), falls man <math>{10}^{N}</math> vorberechnet hat.
In der Realität wählt man dann d=32 und benutzt noch an einigen Stellen modulo Operationen, um die Zahlen nicht zu groß werden zu lassen (siehe die Zahl q in der folgenden Implementation).
Implementation
def searchRabinKarp(text, s):
M, N = len(text), len(s)
d = 32
q = 33554393 # q ist eine große Primzahl, aber so,
# dass d*q < 2**32 (um Überlauf bei 32-bit Integerarithmetik zu vermeiden)
dN = d**N % q # Vorberechnung des Vorfaktors für das Entfernen aus dem Hash
# Initialisierung
hs, ht = 0, 0
for k in range(N):
# ord() gibt die Zeichen-Nummer (z.B. ASCII- oder UTF-8-Code) des
# übergebenen Zeichens zurück
hs = (hs*d + ord( s[k] )) % q
ht = (ht*d + ord(text[k])) % q
# Die Variablen sind jetzt wie folgt initialisiert:
# hs = hash(s)
# ht = hash(text[0:N])
# Hauptschleife
k = 0
while k < M-N:
if hs == ht: # übereinstimmende Hashs => prüfe, dass es nicht nur
# eine Kollision ist
if s == text[k:k+N]: # O(N)-Vergleich nur nötig, wenn Hashs übereinstimmen
return k # search string an Position k gefunden
# nicht gefunden => aktualisiere Hash für den nächsten Teilabschnitt von text:
ht = (d*ht + ord(text[k+N])) % q # neues Zeichen text[k+N] in Hash einfügen
ht = (ht - dN*ord(text[k])) % q # Zeichen text[k] aus Hash entfernen.
k +=1
return -1 # search string nicht gefunden