Suchen

Das Suchen ist eine grundlegende Operation in der Informatik. Viele Probleme in der Informatik können auf Suchaufgaben zurückgeführt werden.

Gemeint ist mit Suchen das Wiederauffinden eines Datensatzes aus einer Menge von früher gespeicherten Datensätzen, oder das Auffinden einer bestimmten Lösung in einem (potentiell großen) Suchraum möglicher Lösungen. Ein paar einleitende Worte zum Suchproblem findet man hier.

Überblick verschiedener Suchprobleme

Um sich der Vielseitigkeit von Suchproblemen bewusst zu werden, ist es sinnvoll, sich einen Überblick über verschiedene Suchmethoden zu verschaffen.

Hier sei auch auf einen bereits existierenden Wikipedia-Artikel zu Suchverfahren verwiesen.

Allen gemeinsam ist die grundlegende Aufgabe, ein Datenelement mit bestimmten Eigenschaften aus einer großen Menge von Datenelementen zu selektieren. Dies kann, natürlich ohne jeden Anspruch auf Vollständigkeit, nach einer der jetzt diskutierten Methoden geschehen:

• Schlüsselsuche: meint das Suchen von Elementen mit bestimmtem Schlüssel; ein klassisches Beispiel wäre das Suchen in einem Wörterbuch, die Schlüssel entsprechen hier den Wörtern, die Datensätze wären die zu den Wörtern gehörigen Eintragungen.

• Bereichssuche: Im Allgemeinen meint die Bereichssuche in n-Dimensionen die Selektion von Elementen mit Eigenschaften aus einem bestimmten n-dimensionalen Volumen. Im eindimensionalen Fall will man alle Elemente finden, deren Eigenschaft(en) in einem bestimmten Intervall liegen. Die Verallgemeinerung auf n-Dimensionen ist offensichtlich. Ein Beispiel für die Bereichssuche in einer 3D-Kugel wäre ein Handy mit Geolokalisierung, welches alle Restaurants in einem Umkreis von 500m findet. Lineare Ungleichungen werden graphisch durch Hyperebenen repräsentiert. In 2D sind diese Hyperebenen Geraden. Die Ungleichungen können dann den Lösungsraum in irgendeiner Form begrenzen.

• Ähnlichkeitssuche: Finde Elemente, die gegebenen Eigenschaften möglichst ähnlich sind. Ein prominentes Beispiel ist Google (=Ähnlichkeit zwischen Suchbegriffen und Dokumenten) oder das Suchen des nächstengelegenen Restaurants (Ähnlichkeit zwischen eigener Position und Position des Restaurants). Ein wichtigster Spezialfall ist die nächste-nachbar Suche.

• Graphensuche: Hier wäre beispielsweise das Problem optimaler Wege zu nennen (Navigationssuche). Dieser Punkt wird später im Verlauf der Vorlesung noch einmal aufgegriffen werden.

Im jetzt Folgenden wird nur noch die Schlüsselsuche betrachtet werden.

Sequentielle Suche

Die sequentielle oder lineare Suche ist die einfachste Methode, einen Datensatz zu durchsuchen. Hierbei wird ein Array beispielsweise sequentiell von vorne nach hinten durchsucht. Ein prinzipieller Vorteil der Methode ist, dass auf der Eigenschaft der Datenelemente, nach denen das Array durchsucht wird, keine Ordnung im Sinne von > oder < definiert zu sein braucht, lediglich die Identität (==) muss feststellbar sein. Der folgende (Pseudo)-Python-Code zeigt eine Implementation der Suchmethode.

a = ... # array

foundIndex = sequentialSearch(a, key) 
# foundIndex == -1 wenn nichts gefunden, 0 <math>\leq </math> foundIndex < len(a) wenn key gefunden (erster Eintrag mit diesem Wert)

def sequentialSearch(a, key):
   for i in range(len(a)):
       if a[i] == key:  # bzw. allgemeiner a[i].key == key 
           return i
   return -1

Wir wollen jetzt die Komplexität dieses Algorithmus bestimmen, wobei die Problemgröße durch N = len(a) gegeben ist.

Dabei nimmt man an, dass der innerste Vergleich (a[i] == key) jeweils <math> \mathcal{O}(1)</math> ist (diese Annahme könnte verletzt sein, wenn der Vergleichsoperator überladen ist und dadurch eine höhere Komplexität hat). Dieser Vergleich wird in der for-Schleife jeweils N-mal durchgeführt (<math> \mathcal{O}(N)</math>), so dass man nach der Verschachtelungsregel eine gesamte Komplexität von <math> \mathcal{O}(N)</math> erhält.

Der Name lineare Suche rührt von diesem linearen Anwachsen der Komplexität mit der Arraygröße her.

Binäre Suche

Wie wir weiter unten zeigen werden, gestattet es diese Suchmethode, die Gesamtdauer der Suche in großen Datensätzen beträchtlich zu verringern. Die Methode beruht auf dem Divide and Conquer-Prinzip, wobei die Suche in jedem Schritt rekursiv auf eine Hälfte des Datensatzes eingeschränkt wird. Weitere Details zur Methode sind hier zu finden.

Die Methode ist nur dann anwendbar beziehungsweise effektiv, wenn folgendes gilt:

1. Auf der Eigenschaft der Daten, die zur Suche verwendet wird, ist eine Ordnung im Sinne von < oder > definiert.
2. Wir wollen uns auf Datensätze beschränken, die schon fertig aufgebaut sind, in die also keine neuen Elemente mehr eingefügt werden, wenn man mit dem Suchen beginnt. Ist dies nicht der Fall, so ist unter Umständen die Implementierung über einen Binärbaum (siehe auch weiter unten) geschickter.

Der folgende Algorithmus zeigt eine beispielhafte Implementierung der Methode (wir setzen wieder N = len(a)):

a = [...,...]     # array
a.sort()   # sortiere über Ordnung des Schlüssels
foundIndex = binSearch(a, key, 0, len(a))  # (Array, Schlüssel, von wo bis wo suchen im Array)
# foundIndex == -1 wenn nichts gefunden, 0 <math>\leq</math>  foundIndex < len(a) wenn key gefunden (erster Eintrag mit diesem Wert)

def binSearch(a, key, start, end):  # start ist 1. Index, end ist letzter Index + 1
   size = end - start   # <math> \mathcal{O}(1)</math>
   if size <= 0:   # Bereich leer?  <math> \mathcal{O}(1)</math>
       return -1   # <math> \mathcal{O}(1)</math>
   center = (start + end)/2   # Integer Division, Ergebnis wird abgerundet, wichtig für ganzzahlige Indizes <math> \mathcal{O}(1)</math>
   if a[center] == key:  # <math> \mathcal{O}(1)</math>
       return center  # <math> \mathcal{O}(1)</math>
   elif a[center] < key:  <math> \mathcal{O}(1)</math>
       return binSearch(a, key, center + 1, end)  # Rekursion
   else:
       return binSearch(a, key, start, center)  # Rekursion

Zur Berechnung der Komplexität dieses Algorithmus vernachlässigen wir zunächst den Aufwand, den die Sortierung weiter oben verursacht. Dieser Schritt mag oder mag nicht zulässig sein.

Nach der Sequenzregel haben auch alle <math>\mathcal{O}(1)</math> Anweisungen die Komplexität <math>\mathcal{O}(1)</math>. Es bleibt die Komplexität der Rekursion zu berechnen. Die gesamte Komplexität des Algorithmus (jetzt als Funktion f bezeichnet) setzt sich zusammen aus den oben erwähnten <math>\mathcal{O}(1)</math> Anweisungen sowie der Rekursion und ist

<math>f(N) = \mathcal{O}(1) + f(N/2) = \mathcal{O}(1) + \mathcal{O}(1) + f(N/4) = ... = \underbrace{\mathcal{O}(1) + ... + \mathcal{O}(1) + \underbrace{f(0)}_{\mathcal{O}(1)\, \rightarrow \,\mathrm{size-Abfrage}}}_{n+1 \,\mathrm{Terme}} </math>

Falls jetzt gilt <math> N = 2^n </math>

<math> \rightarrow f(N) = \mathcal{O}(1) \cdot \mathcal{O}(n+1) = \mathcal{O}(n) = \mathcal{O}(\lg N) </math>

Für große Datenmengen ist die binäre Suche also weit effizienter als die lineare Suche. Verdoppelt sich beispielsweise die zu durchsuchende Datenmenge, so verdoppelt sich der Aufwand für die sequentielle Suche - bei der binären Suche hingegen benötigt man lediglich eine zusätzliche Vergleichsoperation.

Für kleine Daten (<math> N = 4,\, 5 </math>) ist die sequentielle Suche jedoch schneller als die binäre Suche, da hier die rekursiven Funktionsaufrufe teurer als das Mehr an Vergleichen sind. Ein anderer ungünstiger Fall ist gegeben, wenn nur sehr wenige Suchanfragen erfolgen (weniger als <math>\mathcal{O}(N)</math> viele). Dann wird der Aufwand durch das Sortieren des Arrays dominiert, ist also <math>\mathcal{O}(N \lg N) </math>. Auch dann ist sequentielle Suche vorzuziehen.

Eine relativ einfache Möglichkeit, die binäre Suche zu verbessern, ist die sogenannte Interpolationssuche. Hierbei wird die neue Position für die Suche, also die Mitte des Arrays, durch eine Schätzung ersetzt, die angibt, wo sich der Schlüssel innerhalb des Arrays befinden könnte. Bei der Suche in einem Telefonbuch nach dem Namen Zebra würde man ja auch nicht in der Mitte anfangen. Näheres hierzu im Buch von Sedgewick.

Um sich den Algorithmus der binären Suche klar zu machen, ist es instruktiv, sich die folgende Tabelle genauer anzusehen, die die sukzessive Belegung der Variablen bei verschiedenen Anfragen beschreibt. Die Testfälle wurden nach dem Prinzip des domain partitioning gewählt. Das zugehörige Array hat die Einträge

a = [2, 3, 4, 5, 6]

gesuchter key	start	end	size	center	return (-1 oder index)	Kommentare
4	0	5	5	2	2	gefunden
2	0	5	5	2		linker Randfall
	0	2	2	1
	0	1	1	0	0	gefunden
1	0	5	5	2		links außerhalb
	0	2	2	1
	0	1	1	0
	0	0	0		-1	nichts gefunden
6	0	5	5	2		rechter Randfall
	3	5	2	4	4	gefunden
5	0	5	5	2		typischer Fall
	3	5	2	4
	3	4	1	3	3	gefunden
7	0	5	5	2		rechts außerhalb
	3	5	2	4
	5	5	0		-1	nichts gefunden

Suche in einem Binärbaum

Eine kurze Einführung in Binärbäume findet man hier.

Bäume sind zweidimensional verkettete Strukturen. Sie gehören zu den fundamentalen Datenstrukturen in der Informatik. Da man in Bäumen nicht nur Daten speichern kann, sondern auch relevante Beziehungen der Daten untereinander, festgelegt über eine Ordnung auf der vergleichenden Dateneigenschaft (Schlüssel), eignen sich Bäume also insbesondere, um gesuchte Daten schnell wieder auffinden zu können.

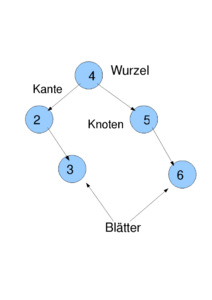
Ein Binärbaum wie oben skizziert besteht aus einer Menge von Knoten, die untereinander durch Kanten verbunden sind. Jeder Knoten hat einen linken und einen rechten Unterbaum, der auch leer sein kann (in Python ließe sich dies mit None implementieren). Führt eine Kante von Knoten A zu Knoten B, so heißt A Vater von B und B Kind von A. Es gibt genau einen Knoten ohne Vater, den man Wurzel nennt. Knoten ohne Kinder heißen Blätter.

Ein Suchbaum hat zusätzlich die Eigenschaft, dass die Schlüssel jedes Knotens sortiert sind. Alle Schlüssel im linken Unterbaum sind kleiner, alle Schlüssel im rechten Unterbaum sind größer als ihr Vater. Wir wollen hierbei annehmen, dass jeder Schlüssel pro Datensatz nur einmal vorkommt, da sich sonst die >- oder <-Relation nicht mehr strikt erfüllen ließe.

Um in einem Baum suchen zu können, wollen wir von zwei Annahmen ausgehen:

1. Einfügen und Suchen im Baum wechseln sich ab. (Wenn das Suchen erst beginnt, nachdem alle Einfügungen erfolgt sind, wäre ein dynamisches Array mit binärer Suche wie oben wesentlich einfacher.)
2. Der Schlüssel, der die Anordnung bestimmt, kennt eine Ordnung (<-Relation oder >-Relation).

Der folgende Python-Code zeigt beispielhaft, wie man in einem Suchbaum suchen könnte. Der Konstruktor für einen Knoten des Suchbaums ließe sich zum Beispiel so implementieren:

class Node:
    def __init__(self, key):
        self.key = key
        self.left = self.right = None

root = ...    # Wurzel des Suchbaums
nodeFound = treeSearch(root, key)   # None, falls nichts gefunden

def treeSearch(node, key):
    if node is None:
        return None
    elif node.key == key:
        return node
    elif key < node.key:
        return treeSearch(node.left, key)
    else:
        return treeSearch(node.right, key)

Daraus resultiert der folgende Suchalgorithmus:

def treeSort(node,array):     # dynamisches Array als 2. Argument
    if node is None:     # <math>\mathcal{O}(1)</math>
        return None:
    treeSort(node.left, array)     # rekursiv
    array.append(node.key)     # <math>\mathcal{O}(1)</math>
    treeSort(node.right, array)     # rekursiv

Komplexität:

<math>
f(N)=\mathcal{O}(1)+f(N_\mathrm{left})+f(N_\mathrm{right})=\mathcal{O}(1)+\mathcal{O}(1)+f(N_\mathrm{leftleft})+f(N_\mathrm{leftright})+\mathcal{O}(1)+f(N_\mathrm{rightleft})
+f(N_\mathrm{leftright})=N\ast\mathcal{O}(1)=\mathcal{O}(N)
</math>

Sortier-Pseudocode:

Sortieren:
    (Array) a     # unsortiert
    (tree) t     # zunächst leer
(dynamisches Array) r     # später sortiert
for e in a:
    t = treeInsert(t, e)
treeSort(t, r)

Insert

Was passiert wenn der key (Schlüssel) schon vorhanden ist?

• error (exception)
• nichts einfügen
• nichts einfügen aber einen boolean return zurückgeben (einfügen=true, false)
• nochmals eingefügt (z.B. in der Node Klasse)

Wobei die ersten 3 Punkte zur Mengensemantik gehören und der letzte eine Multimenge ist.

Algorithmus im zweiten Fall (nichts einfügen):

def treeInsert(node, key):
    if node is None:
        return Node(key)     # Alternative Schreibweise: node = Node(key)
    if node.key == key:      # und dann:
        return node          # pass
    elif key < node.key:     # links im Baum
        node.left = treeInsert(node.left, key)
    else:
        node.right = treeInsert(node.right, key)
    return node

Remove

Fälle:

1. key (bzw. Knoten der key enthält) ist ein Blatt => einfach löschen
2. node hat nur linken Unterbaum oder nur rechten Unterbaum => durch Unterbaum ersetzen
3. node hat beide Unterbäume:
   • Suche Vorgänger: max k < key (k <math>\in</math> keys); Vorgänger ist immer ein Fall 1 oder Fall 2

     => ersetze node durch Vorgänger und entferne Vorgänger

def treePredecessor(node):     # wird nur bei Fall 3 aufgerufen
    node = node.left
    while node.right is not None:
        node = node.right
    return node

def treeRemove(node, key):
    if node is None:
        return node
    if key < node.key:
        node.left = treeRemove(node.left, key)
    elif key > node.key:
        node.right = treeRemove(node.right, key)
    else:
        if node.left is None and node.right is None:     # Fall 1
            node = None
        elif node.left is None:     # Fall 2
            node = node.right       # +
        elif node.right is None:    # Fall 2
            node = node.left
        else:
            pred = treePredecessor(node)
            node.key = pred.key
            node.left = treeRemove(node.left, pred.key)
    return node

Komplexitätsanalyse

• Pfad (Zwischen node₁ und node₂):
  • Folge von Knoten (node_k1,...,node_kn), sodass:
    • node_k1 == node₁
    • node_kn == node₂
    • node_ki und node_ki+1 haben eine gemeinsame Kante.

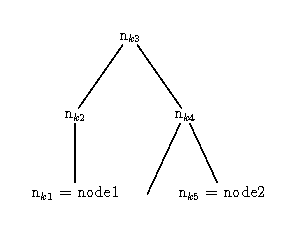(Ein Baum ist ein Graph, indem es zwischen beliebigen Knoten stets genau einen Pfad gibt.)

• Länge eines Pfades: Anzahl der Kanten = Anzahl der Knoten - 1
• Tiefe eines Knotens: Pfadlänge vom Knoten zur Wurzel des Baumes.
• Tiefe des Baumes: maximale Tiefe eines Knotens
• Balance eines Baumes: maximale Tiefe(k) - minimale Tiefe(k) (k <math>\in</math> Blätter)

Ungünstigster Fall von treeSearch

Komplexität von treeSearch = Länge des Pfades zum Knoten wo key gefunden wird, oder erkannt wird, dass key nicht im Baum ist.
=> Ungünstigster Fall: key wird nicht gefunden, aber für diese Entscheidung muss der Längste Pfad vollständig durchlaufen werden.
=> Ungünstigster Fall: <math>\mathcal{O}(T)</math> wo T = Tiefe des Baumes

• [1,2,3,4,5]:
  

  Tiefe T = 4, Balance = 4

=> Ungünstigster Fall: <math>\mathcal{O}(N)</math> wo N = Anzahl der Elemente.

Balance eines Suchbaumes

Balance eines Baumes zu definieren:

• betrachte None als zusätzlichen Knoten : sentinel (engl. für Wächter)
• oder defeniere speziellen sentinel-Knoten
• RS - Pfades : von root → sentinel
• Länge eines Pfades P |P|
• die Balance eines Baumes zu defenieren:

B = max P <math> \in </math> {RS} |P| - min |P|

{RS} Menge aller RS-Pfade

vollständiger Baum

Balance <math>~=0</math>

Alle Knoten(außer Blättern) haben 2 Kinder.

perfect balancierter Baum

Balance <math> \le</math> 1

alternative Defenition für perfect balancierte Bäume

Für jeden Teilbaum gilt es: rechtes und linkes Kind (für jeden Knoten) sind auch wieder perfect balancierte Bäume und ihre Höhe unterscheidet sich höchstens um 1.

Größe

Größe des vollständigen Baumes

Ebene K hat 2 ^k Knoten. Falls Tiefe = d , dann N = 2⁰ + 2¹.....+ 2^d = 2^d+1 -1

Größe des perfect balancierten Baumes

Die Tiefe d, kann nicht besser sein als vollständiger Baum

=>N <math> \le</math> 2 ^d+1 - 1

schlechteste perfect balancierter Baum

ist ein vollständiger der Tiefe d - 1 + 1, N <math> \ge</math> 2^d

=> 2^d <math> \le</math> N <math> \le</math> 2^d+1 - 1

log₂2^d <math>\le</math> log₂N <math>\le</math> log₂(2^d+1 -1) <math>~<</math> log₂(2^d+1)

d <math>\le</math> log₂ N <math>\le</math> (d + 1)

• Ergibt die Komplexität der Suche im schlechtesten Fall: Anzahl der Vergleiche pro Knoten( = 2 bzw. = 3)<math>\ast</math>Anzahl der Knoten

<math>\Rightarrow ~f(N)\le 2d \le 2\log_{2}{ N} = \mathcal{O}(\log_{2}{N})</math>

• perfekt balancierter Baum => AVL-Baum
• balancierter Baum:

<math>\forall N:d(N)\le c \ast d (N)</math> und <math>1 \le c < \mathcal {1}</math>

d ist die Tiefe von perfekt balancierten Baum

Komplexität der Suche:<math> ~f(N)\le c\ast 2\log_{2}{ N} = \mathcal{O}(\log_{2}{N})</math>

algorithmisch einfacher als perfekt balancierter Baum, aber fast genauso schnell

Selbst-Balancierende Suchbäume

Minimiere Balance (erzeuge balancierten Baum):

1. Einfügen in geschickter Reihenfolge (siehe Übungsaufgabe)
2. Selbstbalancierter Baum:
   • Überprüfen der Balance nach jedem Einfügen
   • Umstrukturieren des Baumes, falls Balance > 1 (Suchbaum-Bedingung muss erhalten bleiben)
   • AVL-Bäume (älteste Variante)
   • Rot-Schwarz-Bäume (verbreiteste Variante)
   • Treaps (flexibelste Variante, siehe Übung)
   • Splay trees
   • Andersson Trees (einfachste Variante)

(#* Skip Lists (schnellste Variante, aber kein Binärbaum))

Umstrukturieren, so dass Suchbaumbedingung erhalten bleibt:

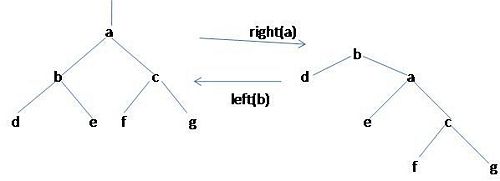
Rotation: elementare Umstrukturierungen

def rotateRight(node):
    newRoot = node.left
    node.left = newRoot.right
    newRoot.right = node
    return newRoot

def rotateLeft(node):
    newRoot = node.right
    node.right = newRoot.left
    newRoot.left = node
    return newRoot

 def insertTree(node,key):
   if node is sentinel:       #(None = sentinel)
       return Node(key)       
   if node.key == key:
       return Node
   if key < node.key:
       Node = insertTree(node.left, key)
   else:
       node.right = insertTree(node.right, key)
  #optimiere Balance:
       return node

Anderson-Bäume

 class Node:
   def__init__(self, key):
       self.key = key
       self.left = selft.right = None
       #einfügen:
       self.level = 1

level : kodiert Abstand von sentinel

Regeln

Es gibt vertikale Kanten(parent.level == child.level + 1 ) und horizontale Kanten(parent.level == child.level)

• verfeinerter Regel : level kodiert reduzierten Abstand von Setinel (d.b. horizontale Kanten werden nicht gezählt)

(die nächste zwei Regeln sichern die Balance):

• alle RS-Pfade haben die gleiche reduzierte Länge oder root hat bei allen Pfaden das gleiche Level
• kein Pfad hat 2 aufeinanderer folgende horizontale Kanten

• nur Kanten zum rechten Kind dürfen horizontal sein
• die reduzierte Höhe jedes Blatts ist hr=1

Beweis

Vereinfachung des Algorithmus

Satz:ein Anderson-Baum ist balanciert.

• 1. Sei hr- die reduzierte Höhe

<math>\Rightarrow</math> jeder Teilbaum enthält mindestens <math>N\ge 2^{hr} -1 </math> Knoten

a). Blätter : reduzierte Höhe 1 => <math> N\ge 2^{1} - 1 = 1</math>

b). inneren Knoten: jeder Unterbaum hat mindestens reduzierte Höhe <math> ~hr - 1 </math>

<math>\Rightarrow</math> jeder Unterbaum hat mindestens <math> ~2^{hr} -1 </math> Knoten

<math>\Rightarrow</math> <math>N \ge 2 (2^{hr-1} -1)+1 = 2^w - 2 + 1 = 2^{hr} -1</math>

alle RS-Pfade heben gleiche Länge

• 2. Kein Pfad hat 2 aufeinanderfolgende horizontal Kanten

<math>\Rightarrow d \le 2 hr + 1</math>

• 3. zusammen:

<math>N \ge 2^{\frac {d}{2}} - 1 </math>

<math>log_{2}{ N}+1\ge log 2^{\frac {d}{2}} - 1 \ge \frac {d}{2}</math>

<math> ~d < 2 log_{2}{(N + 1)}</math> - balancierter Baum

Suchzeit : <math> ~ f(N) = \mathcal{O}(log{N})</math>

Wie erreicht man die Balance

Rotation

  def rotateRight (node):
     root = node.left
     node.left = root.right
     root.right = node
     return root
  def rotateLeft(node):
     root = node.right
     node.right = root.left
     root.left = node
     return root

Optimierung der Balance

      if node.left is not sentinel and node.level==node.left.level:
           node > rotateRight(node)
      if node.right is not sentinel and node.right.right is  not sentinel and node.level==rotate.right.right.level:
           node = rotateLeft(node)
           node.level += 1

---

Sortieren als Suchproblem

Systematisches Fragen mit True und False kann auch als Baum dargestellt werden.

Hier ein Beispiel.Als Eingabe sind drei Zahlen angegeben a={1,2,3},wobei die Reihenfolge nicht bekannt ist.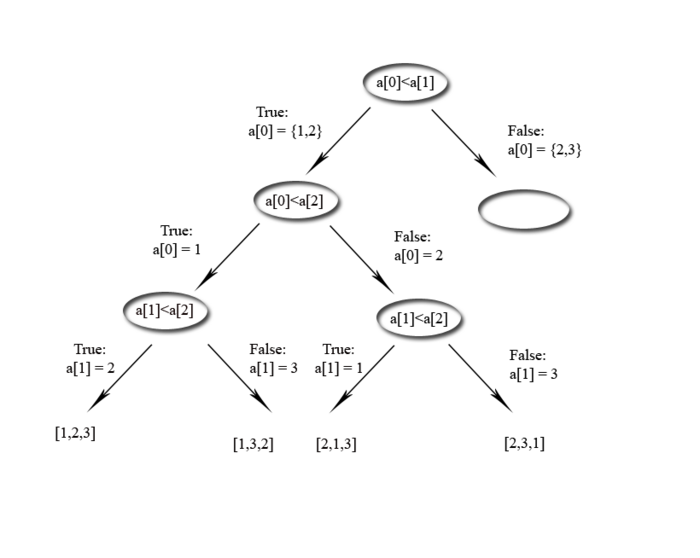

Also mit Eingabe von drei Elemnten müssen im ungünstigsten Fall drei Schritte vorgenommen werden.
Die allgemeine Regel lautet: es gibt N mögliche Lösungen
=>der Baum muss N Blätter haben
=>ein baum mit N Blättern hat mindestens die Höhe logN

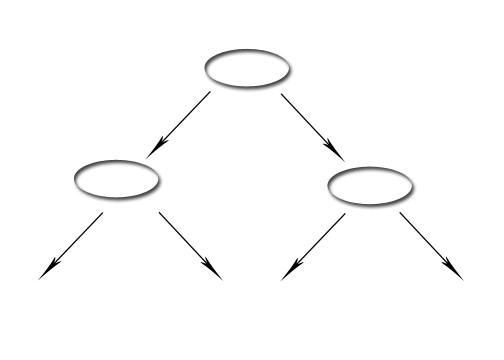
vollständiger Baum (oder balancierter Baum)[1]
2^d+1 Knoten
2^d Blätter

Sortieren

N = n!wenn das Arrey n Elemente hat
Zum Beispiel: 3! = 1*2*3 = 6
log6 <math>\approx</math> 2,6 => d = 3 - bei dem Frage-Baum brauch man im ungünstigsten Fall drei Schritte (True/False)
log6 <math>\approx</math> 2,6 - weil nicht jeder Pfad zu Ende durchgelaufen sein soll, um die Lösung zu bekommen.
d<math>\ge</math>log<math>_2</math>n! = log<math>_2</math>(1,2...n) = log<math>_2</math>1 + log<math>_2</math>2 + ... + log<math>_2</math>n = <math>\sum_{n=1}^n log_2n </math>

Abschätzung von Summen durch Integrale

gegeben : f(x) - monoton wachsend

<math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lfloor x \big\rfloor)dx</math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(x)dx </math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lceil x \big\rceil)dx</math>

<math>\downarrow</math>

<math>\textstyle \int\limits_{x_1}^{x_1 + 1} \underline{f(x_1)}dx</math> + ...+ <math>\textstyle \int\limits_{x_2-1}^{x_2} f(x_2 - 1)dx </math> = <math>\sum_{k=x_1}^{x_2-1} f(k)</math>
( angenommen <math>x_1</math> und <math>x_2</math> <math>\in </math> <math>\mathbb{N},\mathbb{Z}</math> )

wobei f(<math>x_1</math>) = f(<math>\big\lfloor x \big\rfloor </math><math>)_{x_1}^{x_1 +1}</math>

<math>\textstyle \int\limits_{x_1}^{x_1 +1} f(x_1)dx</math> = f(<math>x_1</math>) <math>\textstyle \int\limits_{x_1}^{x_1 + 1} 1dx</math> = f(<math>x_1</math>)x<math>\textstyle \int\limits_{x_1}^{x_1 + 1}</math> = f(x_1)

<math>\sum_{k=x_1}^{x_2-1} f(k) \le \textstyle \int\limits_{x_1}^{x_2} f(x)dx</math>

<math>\sum_{k=x_1 +1}^{x_2} f(k) \ge \textstyle \int\limits_{x_1}^{x_2} f(x)dx \iff</math> <math>\sum_{k=x_1}^{x_2} f(x) \ge \textstyle \int\limits_{x_1 - 1}^{x_2} f(x)dx </math>

für uns gilt: f(x) = log<math>_2</math>(x)

log<math>_2</math>1 + <math>\sum_{k=2}^{n} log_2 x\ge\textstyle \int\limits_{1}^{n} log_2 (x)dx </math> = <math>\frac{1}{ln2}\textstyle \int\limits_{1}^{n} log(x)dx</math> = <math>\frac{1}{ln2}</math> [xlogx - x]<math>_{x = 1}^n</math> = nlog<math>_2</math>(n) - <math>\frac{n - 1}{ln2}</math> = <math>\Omega</math>(nlog<math>_2</math>n)

<math>\Rightarrow</math> d = log<math>_2</math>n! = <math>\Omega</math>(nlogn)

kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymthotisch schneller als Mergesort