Prioritätswarteschlangen: Difference between revisions
No edit summary |
No edit summary |
||
| Line 85: | Line 85: | ||
'''<math>\Rightarrow</math> d = log<math>_2</math>n! = <math>\Omega</math>(nlogn)''' | '''<math>\Rightarrow</math> d = log<math>_2</math>n! = <math>\Omega</math>(nlogn)''' | ||
kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymthotisch schneller als Mergesort | kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymthotisch schneller als Mergesort | ||
==Prioritätswarteschlangen== | |||
* Max Priority Quene : insert(x) | |||
x = largest() | |||
removeLargest() | |||
* Min Priority Quene: smallest() | |||
REMOVEsMALLEST() | |||
===Prioritätswarteschlange als Suchproblem=== | |||
*Sequentielle Suche - Array mit Prioritäten : insert(x)<=> a.append(x) ( <math>\mathcal{O}(1)</math>(amortisierte Komplexität)) | |||
def largest(a):<br> | |||
if len (a) == 0: <br> | |||
raise RuntimeError("...")<br> | |||
''' max = a[0]'''<br> | |||
'''k = 0<br>''' | |||
'''for n in range(1, len(a):''' ''(innere Schleife von SelectionSort)''<br> | |||
''' if a[n] > max''' (Das ganze hat die Komplexität:''' N = len(a) =>''' <math>\mathcal{O}(N)</math><br> | |||
''' man = a[n]'''<br> | |||
''' k = n'''<br> | |||
''' return k'''<br> | |||
Bei kleine Array ist dies die schnellste Methode | |||
Revision as of 02:21, 2 June 2008
Prioritätswarteschlangen
Heap
- Datenstruktur optimiert für Prioritätssuche
- Def: ein linkslastiger Binärbaum ist ein Baum mit <math>d(node.left) \geq d(node.right)</math>
Ein Heap ist ein linkslastiger, perfekt balancierter Baum.
Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht:
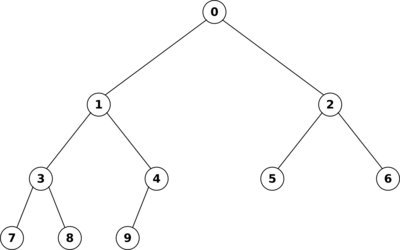
Sortieren als Suchproblem
Systematisches Fragen mit True und False kann auch als Baum dargestellt werden.

Hier ein Beispiel.Als Eingabe sind drei Zahlen angegeben a={1,2,3},wobei die Reihenfolge nicht bekannt ist.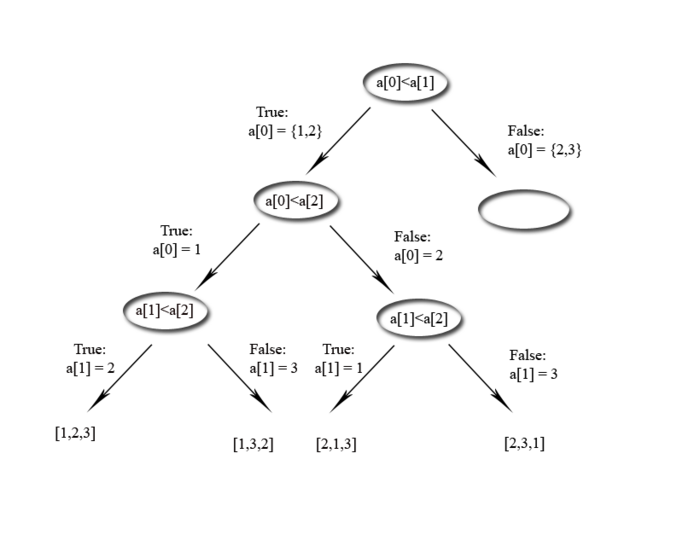
Also mit Eingabe von drei Elemnten müssen im ungünstigsten Fall drei Schritte vorgenommen werden.
Die allgemeine Regel lautet: es gibt N mögliche Lösungen
=>der Baum muss N Blätter haben
=>ein baum mit N Blättern hat mindestens die Höhe logN
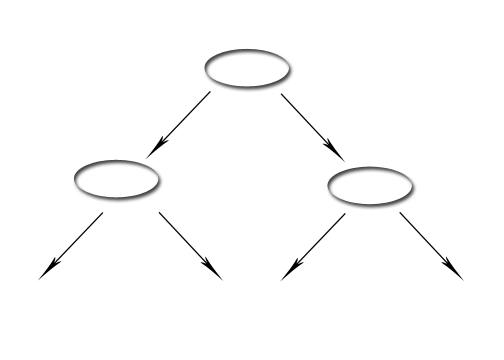
vollständiger Baum (oder balancierter Baum)[1]
2^d+1 Knoten
2^d Blätter
Sortieren
N = n!wenn das Arrey n Elemente hat
Zum Beispiel: 3! = 1*2*3 = 6
log6 <math>\approx</math> 2,6 => d = 3 - bei dem Frage-Baum brauch man im ungünstigsten Fall drei Schritte (True/False)
log6 <math>\approx</math> 2,6 - weil nicht jeder Pfad zu Ende durchgelaufen sein soll, um die Lösung zu bekommen.
d<math>\ge</math>log<math>_2</math>n! = log<math>_2</math>(1,2...n) = log<math>_2</math>1 + log<math>_2</math>2 + ... + log<math>_2</math>n = <math>\sum_{n=1}^n log_2n
</math>
Abschätzung von Summen durch Integrale
gegeben : f(x) - monoton wachsend

<math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lfloor x \big\rfloor)dx</math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(x)dx
</math> <math>\le</math> <math>\textstyle \int\limits_{x_1}^{x_2} f(\big\lceil x \big\rceil)dx</math>
<math>\downarrow</math>
<math>\textstyle \int\limits_{x_1}^{x_1 + 1} \underline{f(x_1)}dx</math> + ...+ <math>\textstyle \int\limits_{x_2-1}^{x_2} f(x_2 - 1)dx
</math> = <math>\sum_{k=x_1}^{x_2-1} f(k)</math>
( angenommen <math>x_1</math> und <math>x_2</math> <math>\in </math> <math>\mathbb{N},\mathbb{Z}</math>
)
wobei f(<math>x_1</math>) = f(<math>\big\lfloor x \big\rfloor </math><math>)_{x_1}^{x_1 +1}</math>
<math>\textstyle \int\limits_{x_1}^{x_1 +1} f(x_1)dx</math> = f(<math>x_1</math>) <math>\textstyle \int\limits_{x_1}^{x_1 + 1} 1dx</math> = f(<math>x_1</math>)x<math>\textstyle \int\limits_{x_1}^{x_1 + 1}</math> = f(x_1)
<math>\sum_{k=x_1}^{x_2-1} f(k) \le \textstyle \int\limits_{x_1}^{x_2} f(x)dx</math>
<math>\sum_{k=x_1 +1}^{x_2} f(k) \ge \textstyle \int\limits_{x_1}^{x_2} f(x)dx \iff</math> <math>\sum_{k=x_1}^{x_2} f(x) \ge \textstyle \int\limits_{x_1 - 1}^{x_2} f(x)dx
</math>
für uns gilt: f(x) = log<math>_2</math>(x)
log<math>_2</math>1 + <math>\sum_{k=2}^{n} log_2 x\ge\textstyle \int\limits_{1}^{n} log_2 (x)dx
</math> = <math>\frac{1}{ln2}\textstyle \int\limits_{1}^{n} log(x)dx</math> = <math>\frac{1}{ln2}</math> [xlogx - x]<math>_{x = 1}^n</math> = nlog<math>_2</math>(n) - <math>\frac{n - 1}{ln2}</math> = <math>\Omega</math>(nlog<math>_2</math>n)
<math>\Rightarrow</math> d = log<math>_2</math>n! = <math>\Omega</math>(nlogn)
kein Sortieralgorithmus auf Basis paarweise Vergleiche ist asymthotisch schneller als Mergesort
Prioritätswarteschlangen
* Max Priority Quene : insert(x)
x = largest()
removeLargest()
* Min Priority Quene: smallest()
REMOVEsMALLEST()
Prioritätswarteschlange als Suchproblem
- Sequentielle Suche - Array mit Prioritäten : insert(x)<=> a.append(x) ( <math>\mathcal{O}(1)</math>(amortisierte Komplexität))
def largest(a):
if len (a) == 0:
raise RuntimeError("...")
max = a[0]
k = 0
for n in range(1, len(a): (innere Schleife von SelectionSort)
if a[n] > max (Das ganze hat die Komplexität: N = len(a) => <math>\mathcal{O}(N)</math>
man = a[n]
k = n
return k
Bei kleine Array ist dies die schnellste Methode