Prioritätswarteschlangen: Difference between revisions
m (→Heap: Größe der Grafik geändert) |
No edit summary |
||
| Line 8: | Line 8: | ||
Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht: | Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht: | ||
[[Image:heapArray.png|left|400px]] | [[Image:heapArray.png|left|400px]] | ||
==Sortieren als Suchproblem== | |||
Systematisches Fragen mit True und False kann auch als Baum dargestellt werden.<br> [[Image:penka.png|400px]] | |||
Hier ein Beispiel.Als Eingabe sind drei Zahlen angegeben a={1,2,3},wobei die Reihenfolge nicht bekannt ist.<br>[[Image:trueFalseBeisp.png|700px]]<br> Also mit Eingabe von drei Elemnten müssen im ungünstigsten Fall drei Schritte vorgenommen werden.<br>Die allgemeine Regel lautet: es gibt N mögliche Lösungen <br> =>der Baum muss N Blätter haben<br> =>ein baum mit N Blättern hat mindestens die Höhe logN<br>[[Image:vollbaum.png|left]] | |||
vollständiger Baum (oder balancierter Baum)[[Main Page]]<br>2^d+1 Knoten<br>2^d Blätter<br> | |||
==Sortieren== | |||
N = n!wenn das Arrey n Elemente hat<br>Zum Beispiel: 3! = 1*2*3 = 6 <br> log6 <math>\approx</math> 2,6 => d = 3<br>log6 <math>\approx</math> 2,6 ist <math>\approx</math>, weil nicht jeder Pfad zu Ende durchgelaufen sein soll, um die Lösung zu bekommen. | |||
Revision as of 14:49, 31 May 2008
Prioritätswarteschlangen
Heap
- Datenstruktur optimiert für Prioritätssuche
- Def: ein linkslastiger Binärbaum ist ein Baum mit <math>d(node.left) \geq d(node.right)</math>
Ein Heap ist ein linkslastiger, perfekt balancierter Baum.
Man kann einen Heap leicht als Array implementieren, wie folgende Grafik veranschaulicht:
Sortieren als Suchproblem
Systematisches Fragen mit True und False kann auch als Baum dargestellt werden.

Hier ein Beispiel.Als Eingabe sind drei Zahlen angegeben a={1,2,3},wobei die Reihenfolge nicht bekannt ist.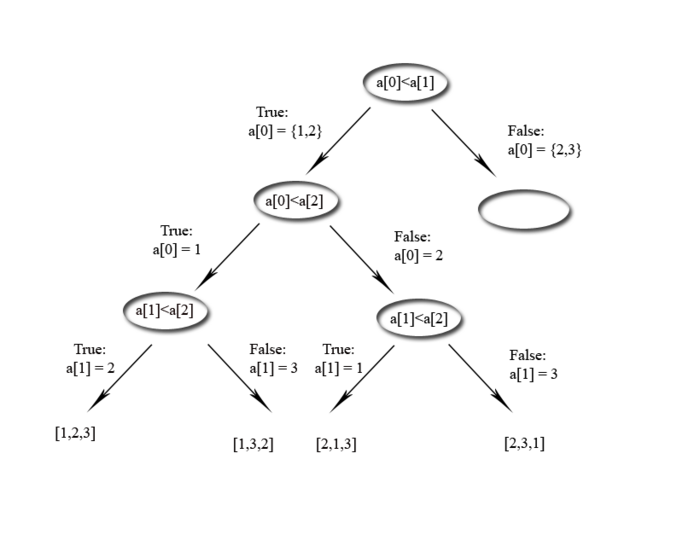
Also mit Eingabe von drei Elemnten müssen im ungünstigsten Fall drei Schritte vorgenommen werden.
Die allgemeine Regel lautet: es gibt N mögliche Lösungen
=>der Baum muss N Blätter haben
=>ein baum mit N Blättern hat mindestens die Höhe logN
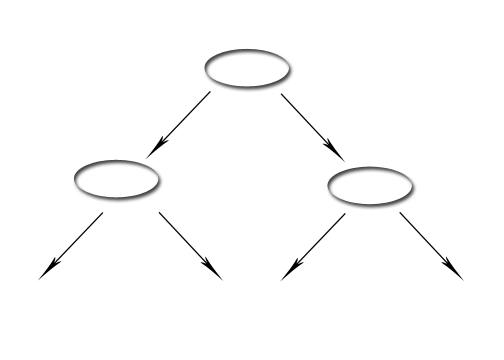
vollständiger Baum (oder balancierter Baum)Main Page
2^d+1 Knoten
2^d Blätter
Sortieren
N = n!wenn das Arrey n Elemente hat
Zum Beispiel: 3! = 1*2*3 = 6
log6 <math>\approx</math> 2,6 => d = 3
log6 <math>\approx</math> 2,6 ist <math>\approx</math>, weil nicht jeder Pfad zu Ende durchgelaufen sein soll, um die Lösung zu bekommen.