Graphen und Graphenalgorithmen

Einführung zu Graphen

Motivation

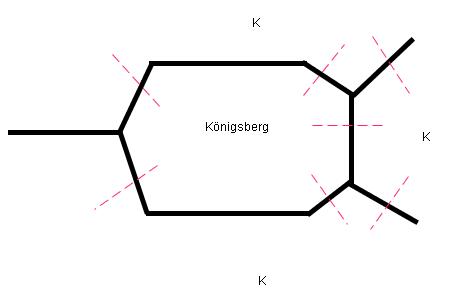
Königsberger - Brückenproblem

(1736 Euler)

Königsberger Brücken:

Spaziergang durch Königsberg, so dass alle Brücken nur einmal überquert werden.

Geometrie: Topologie

    O
   || \
   ||  \
    O   O
   ||  /
   || /
    O

• Definition: ungerichteter Graph

Ein ungerichteter Graph G = ( V, E )

• • V ist endliche Menge von Knoten (vertices)
  • E c V × V (edges)

Ein Graph heißt ungerichtet, wenn zusätzlich gilt:

(x,y) ∈ E => (y,x) ∈ E (symmetrie)

Bsp:

gerichteter Graph

ungerichtet

 O
|| \
||  \
 O   O
||  /
|| /
 O

Bsp:

• Landkarten:
  • Knoten: Länder
  • Kanten: gem. Grenzen

• Schaltkreis:
  • Knoten: Gatter
  • Kanten: Verbindungen

• Chemie (Summenformeln):
  • Knoten: Elemente
  • Kanten: Bindungen

• Soziologie (StudieVZ)
  • Soziogramm
    • Knoten: Personen
    • Kanten: Freund von ...

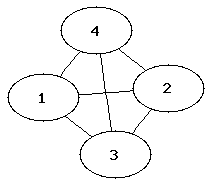
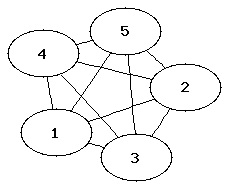
• Definition: Vollständige Graphen

Bei vollständigen Graphen ist jeder Knoten mit allen anderen Knoten verbunden.

E = U V (v,w) u (w,v) | v ∈ V, w ∈ V, u != w

k1	k2	k3
k4	k5

Rätsel Auf einer Party sind Leute. Alle stoßen miteinander an. Es hat 78 mal "Pling" gemacht. Wieviele Leute waren da?

Repräsentation von Graphen

Sei G = ( V, E ) geg und liege V in einer lineraren Sortierung vor. V = { v1, ...., vn }

Adjazenzmatrix

AG = aij = {1 falls (vi, vj) ∈ E ; sonst 0}

Bsp:

v = { a,b,c,d }     b      d
                    | \  / |
                    |  \/  |
                    |  /\  |
                    | /  \ |
                    a      c

      a b c d
     -----------
     (0 1 0 1) |a 
AG = (1 0 1 0) |b
     (0 1 0 1) |c
     (1 0 1 0) |d

Adjezenzlisten

al(v) = {v' ∈ V | (u,u') ∈ E} Lg = ((v1, al(v1)), ...., (vn, al(vn))

Python:

Array von Arrays [[...],[...],...,[...]]
                    0     1         n

• Definition: Teilgraphen

Ein Graph G' = (v',E') ist ein Teilgraph, wenn gilt:

• • v' c V
  • E' c E

Er heißt erzegender Graph, wenn zusätzlich gilt:

• • v' = V

• Definition: Knotengrade

Für G = (v,E)und v ∈ V grad(v) = |{v' ∈ V | v,v'∈ E}| out_grad(v) = | -""- | in_grad(v) = |{v'∈ V| (v',v) ∈ E}|

Bsp:

ungerichtet

 c
|| \
||  \
 b   d          grad(a) = | {b,b,d} | = 3
||  /
|| /
 a

 
gerichtet

 c←
 | \
 ↓  \
 b←--d         out_grad(d) = 2 = | {c,b} |
 |  /→          in_grad(d) = 1 = | {a} |
 ↓ /
 a

• Definition: Wege

Sei G = (v,E)

• • Für v0 ∈ V ist (v0) ein Weg in G
  • Für Knoten v1,...vn,vn+1 und eine Kante (vn,vn+1) ∈ E ist mit einem Weg (v0,....vn) in G auch (v0,...,vn,vn+1) ein Weg in G.

Also: Nichtleere Folgen von Knoten die durch eine Kante verbunden sind.

Eulerweg

   O
  /  \
 O----O
 | \/ |
 | /\ |   "Das Haus vom Nikolaus" Alle Kanten werden nur einmal passiert
 O----O

Hamiltonweg

   O
  /   
 O----O
    /  
   /      Alle Knoten werden nur einmal passiert
 O----O

Kreis

   O
  /  \
 O    O
 |    |   v0 = vn
 |    |   vi != vj   Für Alle i,j   i !=j; i,j >0; i,j < n
 O----O     

Zyklen

   O
  /  \
 O    O
   \  |
    \ |   Wie Kreis nur ohne (vi != vj)
 O====O

• Definition: planare Graphen

Ist ein Graph, der auf einer Ebene gezeichnet werden kann, sodass sich die Kanten nicht schneiden!

Bsp:

1)  

     O
    /|\
   / O \
  / / \ \
  O     O

2)

   O
  /  \
 O----O
 | \/ |
 | /\ |   
 O----O

3)

|----O   @
|   /@ \
|  O----O
|  |@ / |
|  | / @|   
|  O----O               @ entspricht Regionen auch ausserhalb der Figur ist eine Region
|@      |
|-------|

1),2) und 3) sind planare Graphen.

Der K5 Graph ist kein planarer Graph da sich zwangsweise Kanten schneiden.

• Definition: dualer Graph

Der duale Graph eines geg. planaren Graphs G' ist ein Graph mit

• • Knoten für jede Region
  • Für jede Kante aus E gilt es gibt eine Kante, die die angrenzende Region mit Knoten verbindet.

dualer Graph

     O------O
     |     /| \
   |-|-@  / | @\---|
   | | |\/  |/| O  |
   | | |/\ /| |/   |
   | | /  @ | /    |
   | O-+--+-O |    |
   |   |  |   |    |
   |---|--@---|----|

• Definition: erreichbar

W ∈ V ist erreichbar von v ∈ G gdw.:
es Existiert Weg(v,...w)

• Definition: Zusammenhang

G heißt zusammenhängend, wenn für Alle v,w ∈V gilt:
w ist erreichbar von V

Bäume

• Definition: Baum

Ein Baum ist ein zusammenhängender, kreisfreier Graph.

Bsp.: Binary Search Tree

• Definition: erzeugender Baum

für G = (v,E) ist ein erzeigender Teilgraph mit Baumeigenschaft

Bsp.:

   O    O
  /    /   
 O    O    O
 |  /    /   
 | /    /    
 O----O----O

Durchlaufen von Graphen

Tiefensuche in Graphen

Sei der Graph gegeben als Liste von Listen = g

def dfs (g,node,v=0):
  if v == 0:
    v = [0]*len(g) #visited-Liste
  v[node] = 1 #besuche node
  for t in g[node]: #gehe zu allen Nachbarn
    if v[t] == 0: #falls diese noch nicht besucht
      dfs(g,t,v) #Rekursion

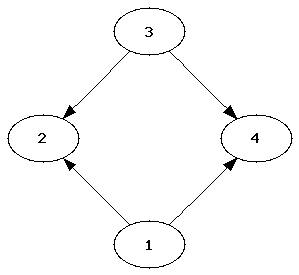
Aufruf dfs(g,1)

=>Folge 1,2,4,3,6,7,5

Breitensuche

from Queue import *
def bfs(g,startnode)
  v = [0]*len(g)
  q = Queue()
  v = [startnode] = 1 #besuche
  q.put(startnode) #in Schlange
  while not q.get()
    node = q.get()
    for t in q[node]
      if v[t] == 0:
        v[t] = 1
        q.put(t)

=>Folge 1,2,3,4,5,6,7

Damenproblem

 ---------------
|   | X |   |   |
|---|---|---|---| 
|   |   |   | X |
|---|---|---|---|
| X |   |   |   |
|---|---|---|---|
|   |   |   | X |
 ---------------

4 Damen auf einem vereinfachten Schachbrett so Positionieren, dass sich keine bedroht.

erster Durchlauf:

zweiter Durchlauf:

Weitere Anwendungen (18.06.08)

def dfs(graph):
       
       Diese Tiefensuche tut so noch nichts weiter als zu traversieren
       + graph ist Array,
           i-ter Eintrag enthaelt Adjazenzliste (auch Array) des i-ten Knotens,
           wobei Knoten nummeriert von 0 ... v-i
       
       def visit(graph, node, visited):
               
               visited ist Array mit Flags fuer besuchte Knoten
               
               if visited[node]: return
               visited[node] = True
               for neighbor in graph[node]:
                       visit(graph, neighbor, visited)

       visited = [False]*len(graph)
       for node in range(len(graph)):
               visit(graph, node, visited)

Finden von Zusammenhangskomponenten

Ein moeglicher Einsatz des Verfahrens ist das Finden von Zusammenhangskomponenten (connected components).

• Beispiel: ...

• Definition: CC_i = {u_k, u_l e V: es gibt einen Pfad von u_k nach u_l ("u_l ist von u_k aus erreichbar")
• fuer ungerichtete Graphen gilt zusaetzlich: es gibt einen Pfad von u_l nach u_k}

Die Relation CC_i, also die Zusammenhangskomponenten (ZK) bilden eine Aequivalenzrelation, also kann fuer jede ZK ein Repraesentant bestimmt werden (der sog. "Anker"). Kennt jeder Knoten seinen Anker, so ist das ZK-Problem geloest.

Tiefensuchen-Algorithmus

Unser erster Ansatz ist, den Anker mit Hilfe der Tiefensuche zu finden, wobei statt Knotenbesuche Knotennummern fuer die schon gefundenen Anker gesetzt werden. Ein moeglicher Algorithmus lautet damit wie folgt:

def connectedComponents(graph):
       def visit(graph, node, anchors, anchor):
               
               anchor ist Anker der aktuellen ZK
               
               if anchors[node] is not None: return # Anker von <node> schon bekannt
               anchors[node] = anchor
               for neighbor in graph[node]
                       visit(graph, neighbor, anchors, anchor)

       anchors = [None]*len(graph)
       for node in range(len(graph)):
               visit(graph, node, anchors, node) # node: Anker der naechste ZK = erster Knoten der ZK
       return anchors

• Beispiel: ...

Union-Find-Algorithmus

Eine Alternative (ohne Tiefensuche) waere z.B. ein Union-Find-Algorithmus. Idee dabei ist, dass eingangs jeder Knoten eine eigene ZK bildet, wobei in einer anschliessenden Rekursion Kanten gesucht werden, die zwischen den ZK bestehen.

Initialisierung: jeder Knoten wird als 1 ZK behandelt Rekursion: fasse ZK zusammen (Union) falls Kante zwischen ihnen existiert Ergebnis: Array mit dem Anker jedes Knotens

def unionFindCC(graph):
       def findAnchor(anchors, k):
               
               Prueft auf anchors[k]==k
               
               while anchors[k] != k:
                       k = anchor[k]
               return k

       def edges(graph):
               e = []
               for node in range(len(Graph)):
                       for n in graph[node]:
                               if node < n:
                                       e.append((node, n))
               return e

       anchors = range(len(graph) # jeder Knoten ist sein eigener Anker
       for edge in edges(graph):
               # diese Schleife ordnet die Anker so, dass
               #   der 1. Anker immer der kleinste ist
               a1, a2 = findAnchor(anchors, edge[0]), findAnchor(anchors, edge[1])
               if a2 < a1: a2,a1 = a1,a2
               if a1 != a2: anchors[a2] = a1
       for node in range(len(graph)):
               # diese Schleife raeumt mit Indirektionen auf (s. Bsp. (#))
               anchor[node] = findAnchor(anchors, node)

• Beispiel (#): ...

Eine verbreitete Anwendung fuer dieses Verfahren gibt es in der Bildverarbeitung:

• Beispiel: ...

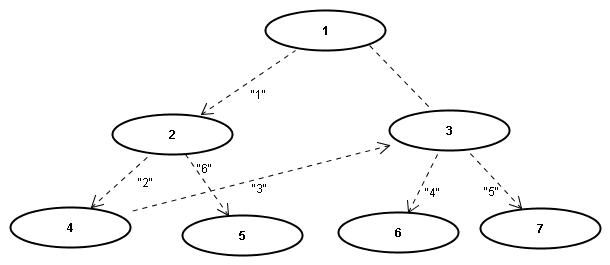
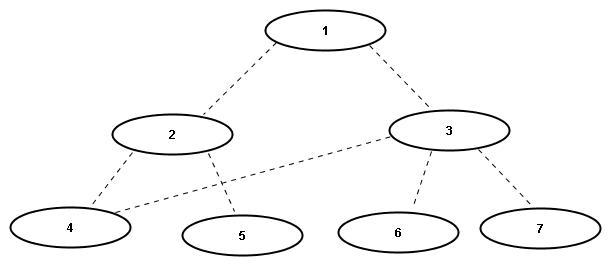
Detektion von Zyklen

Zum Finden von Zyklen, bzw. der Feststellung, ob ein Graph azyklisch ist, verwenden wir wieder eine modifizierte Version der Tiefensuche: diesmal wird die Reihenfolge, in der die Knoten gefunden werden gespeichert. Es gibt einen Zyklus genau dann, wenn man zu einem hinreichend frueher (d.h. nicht zum direkten Vorgaenger) Knoten zurueckkommt.

• Beispiel: ...

def acyclicGraph(graph):               # True, falls keine Zyklen bestehen
       def visit(graph, node, visited, count):
               
               muss gewaehrleisten, dass <visited[node]> den kleinsten
                 von <node> aus mit Tiefensuche erreichbaren Knoten
                 angibt
               
               visited[node] = count
               count += 1
               minVal = visited[node]
               for neighbor in graph[node]:
                       if visited[neighbor] is None:
                               count, minRes = visit(graph, neighbor, visited, count)
                               # minRes ist der kleinste in diesem Aufruf gefundene Knoten
                               if minRes < minVal:
                                       minVal = minRes
                       elif visited[neighbor] < minVal:
                               minVal = visited[neighbor]
               return count, minVal

       visited = [None]*len(graph)
       count = 0                       # Zaehler fuer Reihenfolge
       for node in range(len(graph)):
               if visited[node] is not None:
                       continue
               count, minVal = visit(graph, node, visited, count)
       for node in range(len(graph)):
               if visited[node] < node: return False # Zyklus
       return True

2. Variante von acyclic:

def acyclic2(graph):
   visited = [False]*len(graph)
   for node in range(len(graph)):
       if visited[node]:continue #Kein Zyklus
       if not visit2(graph, node, None, visited): return False
   return True

def visit2(graph, node, fromNode, visited):
   if visited[node]: return False #Zyklus entdeckt
   visited[node] = True #Knoten wird markiert
   for neighbor in graph[node]:
       if neighbor == fromNode: continue #Ueberspringen von fromNode
       if not visit2(graph, neighbor, node, visited): return False #Zyklus weitergeben
   return True #kein Zyklus

Variationen der Tiefensuche (19.06.2008)

Wichtige Algorithmen, die in der Vorlesung nicht behandelt werden

• Max Flow (zur Bestimmung des maximalen Flusses z.B. bei Ölpipelines)
• Matching (auch Paarung genannt): Teilmenge der Kanten eines Graphen, wobei keine zwei Kanten einen gleichen Knoten besitzen

  Anwendungsbereiche: z.B. Arbeitsamt (Zuordnung Arbeitssuchender - Stellenangebot), Universität (Zuordnung Studenten - Übungsgruppen)

Vereinfachte Lösung für den acyclic-Algorithmus

  
    def acyclic(graph):
        def visit(graph, node, fromNode, visited):
            if visited[node]:					# Zyklus entdeckt
                return False
            visited[node] = True
            for neighbor in graph[node]:
                if neighbor == fromNode:			# überspringe fromNode
                    continue
                if not visit(graph, neighbor, node, visited):
                    return False				# der Graph ist zyklisch
            return True						# kein Zyklus
        visited = [False]*len(graph)
        for node in range(len(graph)):
            if visited[node]:			# schließt aus, dass Knoten besucht wird, der schon besucht war
                continue
            if not visit(graph, node, None, visited):
                return False
        return True
  

Anmerkungen zum Code:

• wenn ein Knoten bereits besucht ist, dann gehört er zur gleichen Zusammenhangskomponente - dies hat allerdings nichts mit einem Zyklus zu tun
• ein Graph der einmal zyklisch war wird nie wieder azyklisch
• der obige Algorithmus weist Ähnlichkeiten mit den bereits behandelten Algorithmen auf: ein guter Algorithmus zeichnet sich dadurch aus, dass mit kleinen Code-Variationen ganz andere Probleme gelöst werden können

Kürzeste Wege (Pfade)

• Definition: gewichteter Graph

• jeder Kante e ist eine reelle oder natürliche Zahl w_e zugeordnet (wird auch als Kantengewicht bezeichnet)

• z.B.

• Abstand der Anfangs- und Endknoten

• Durchflusskapazität eines Rohres (für max- Flussprobleme)

• Wechselkurse (Knoten sind Währungen, Kanten sind Wechselkurse; Darstellung in einem gerichteten Graph, da jede Kante auch eine Richtung hat: unterschiedliche Wechselkurse + Bankgebühren)

• Definition: Problem des kürzesten Weges

Sei P die Menge aller Wege von u nach v

Puv = {u_v}

und der Weg gegeben durch

u → x1 → x2 → ... → v

dann sind die Kosten eines Weges definiert durch

Kosten (Puv) = <math>\sum\limits_{l \in Pv}</math> we

• gesucht: Pfad u_v, so dass Kosten (u_v) minimal sind

• Lösung: Algorithmus von Dijkstra

Algorithmus von Dijkstra

Edsger Wybe Dijkstra

geb. 11. Mai 1930 in Rotterdam

ges. 06. August 2002

Dijkstra war ein niederländischer Informatiker und Wegbereiter der strukturierten Programmierung. 1972 erhielt er für seine Leistung in der Technik und Kunst der Programmiersprachen den Turing Award, der jährlich von der Association for Computing Machinery (ACM) an Personen verliehen wird, die sich besonders um die Entwicklung der Informatik verdient gemacht haben. Zu seinen Beiträgen zur Informatik gehören unter anderem der Dijkstra-Algorithmus zur Berechnung des kürzesten Weges in einem Graphen sowie eine Abhandlung über den go-to-Befehl und warum er nicht benutzt werden sollte. Der go-to-Befehl war in den 60er und 70er Jahren weit verbreitet, führte aber zu Spaghetti-Code. In seinem berühmten Paper "A Case against the GO TO Statement", das als Brief mit dem Titel "Go-to statement considered harmful" veröffentlicht wurde, argumentiert Dijkstra, dass es umso schwieriger ist, dem Quellcode eines Programmes zu folgen, je mehr go-to-Befehle darin enthalten sind und zeigt, dass man auch ohne diesen Befehl gute Programme schreiben kann.

Algorithmus

 
   import heapq	# heapq ist ein Modul von Python
   def dijkstra(graph, start, ziel):	# graph: gewichtete Adjazenzliste
       heap = []
       visited = [None]*len(graph)
       visited[start] = start
       for neighbor in graph[start]:
           heapq.heappush(heap, (neighbor[1], start, neighbor[0])) # neighbor[1]:Kantengewicht,neighbor[0]:Endpunkt d. K.
       while len(heap) > 0:	# solange der heap nicht leer ist
           w, fromNode, node = heapq.heappop(heap)
           if visited[node] is not None:	# wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
               continue
           visited[node] = fromNode    # baue Vorgänger-Baum
           if node == ziel:	# da der heap noch nicht leer ist, wird an dieser Stelle ein break benötigt
               break
           for neighbor in graph[node]:
               if visited[neighbor[0]] is not None:	# wenn der kürzeste Pfad bereits bekannt ist, überspringe ihn
                   continue
               heapq.heappush(heap, (neighbor[1]+w, node, neighbor[0]))
       bestPath = []
       t = ziel
       while t != visited[t]:		# Array wird durchlaufen bis der Anker des Pfades gefunden ist, vgl. Union-Search
           bestPath.append(t)
           t=visited[t]
       bestPath.append(start)
       return bestPath			# bestPath.reverse()