Effizienz

(Vorlesung 7.5.:)

Laufzeit

Die Laufzeit ist für den Benutzer ein wichtiges Kriterium. Schwierigkeit bei der Bestimmung: Die Laufzeit hängt von vielen Faktoren ab die evtl. nicht kontrollierbar sind:

• Prozessor/Auslastung des Systems
• Speicher/Cache/Bus
• Compiler/Optimierer des Compilers (Compiler auf verschiedene Architekturen optimiert?)
• Geschick des Programmierers
• Daten (Beispiel Quicksort: Best case und worst case [vorsortierter Input] stark unterschiedlich)

All diese Faktoren sind untereinander abhängig.

Laufzeitvergleiche sind mit Vorsicht zu interpretieren. Generell sollten bei Vergleichen möglichst wenige Parameter verändert werden, z.B.

• gleiches Programm(gleiche Kompilierung), gleiche Daten, andere Prozessoren

oder

• gleiche CPU, Daten, andere Programme (Vergleich von Algorithmen)

Beobachtung: Durch Laufzeitmessung ist schwer festzustellen, ob ein Algorithmus prinzipiell besser ist als ein anderer.

Komplexität

Komplexitätsbetrachtungen ermöglichen den Vergleich der prinzipiellen Eigenschaften von Algorithmen unabhängig von einer Implementation, Umgebung etc.

Eine einfache Möglichkeit ist das Zählen der Aufrufe einer Schlüsseloperation. Beispiel Sortieren:

• Anzahl der Vergleiche
• Anzahl der Vertauschungen

Beispiel: Selection Sort

 for i in range(len(a)-1):
   max = i
   for j in range(i+1, len(a)):
     if a[j] < a[max]:
       max = j
   a[max], a[i] = a[i], a[max]      # swap

• Anzahl der Vergleiche: Ein Vergleich in jedem Durchlauf der inneren Schleife. Es ergibt sich folgende Komplexität:

  Ingesamt <math>\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1}1 = \frac{N}{2} (N-1) \!</math> Vergleiche.

• Anzahl der Vertauschungen (swaps): Eine Vertauschung pro Durchlauf der äußeren Schleife:

  Insgesamt <math>N-1 \!</math> Vertauschungen

Die Komplexität wird durch die Operationen bestimmt, die am häufigsten ausgeführt werden, hier also die Anzahl der Vergleiche. Die Anzahl der Vertauschungen ist hingegen kein geeignetes Kriterium für die Komplexität von selection sort, weil der Aufwand in der inneren Schleife ignoriert würde.

Fallunterscheidung: Worst und Average Case

Die Komplexität ist in der Regel eine Funktion der Eingabegröße (Anzahl der Eingabebits, Anzahl der Eingabeelemente). Sie kann aber auch von der Art der Daten abhängen, nicht nur von der Menge, z.B. vorsortierte Daten bei Quicksort. Um von der Art der Daten unabhängig zu werden, kann man zwei Fälle der Komplexität unterscheiden:

• Komplexität im ungünstigsten Fall

  Der ungünstigste Fall ist die Eingabe gegebener Länge, für die der Algorithmus am langsamsten ist. Der Nachteil dieser Methode besteht darin, dass dieser ungünstige Fall in der Praxis vielleicht gar nicht oder nur selten vorkommt, so dass sich der Algorithmus in Wirklichkeit besser verhält als man nach dieser Analyse erwarten würde. Beim Quicksort-Algorithmus mit zufälliger Wahl des Pivot-Elements müsste z.B. stets das kleinste oder größte Element des aktuellen Intervalls als Pivot-Element gewählt werden, was äußerst unwahrscheinlich ist.

• Komplexität im durchschnittlichen/typischen Fall

  Der typische Fall ist die mittlere Komplexität des Algorithmus über alle möglichen Eingaben. Dazu muss man die Wahrscheinlichkeit jeder möglichen Eingabe kennen, und berechnet dann die mittlere Laufzeit über dieser Wahrscheinlichkeitsverteilung. Leider ist die Wahrscheinlichkeit der Eingaben oft nicht bekannt, so dass man geeignete Annahmen treffen muss. Bei Sortieralgorithmen können z.B. alle möglichen Permutationen des Eingabearrays als gleich wahrscheinlich angenommen werden, und der typische Fall ist dann die mittlere Komplexität über alle diese Eingaben. Oft hat man jedoch in der Praxis andere Wahrscheinlichkeitsverteilungen, z.B. sind die Daten oft "fast sortiert" (nur wenige Elemente sind an der falschen Stelle). Dann verhält sich der Algorithmus ebenfalls anders als vorhergesagt.

Wir beschränken uns in dieser Vorlesung auf die Komplexität im ungünstigseten Fall. Exakte Formeln für Komplexität sind aber auch dann schwer zu gewinnen, wie das folgende Beispiel zeigt:

Beispiele aus den Übungen (Gemessene Laufzeiten für Mergesort/Selectionsort)

• Mergesort: <math>\frac{0,977N\log N}{\log 2} + 0,267N-4.39 \!</math>

  andere Lösung: <math>1140 N\log(N) - 1819N + 6413 \!</math>

• Selectionsort: <math>\frac{1}{2}N^2 - \frac{1}{2N} - 10^{-12} \!</math>

  andere Lösung: <math>1275N^2 - 116003^N + 11111144 \!</math>

Aus diesen Formeln wird nicht offensichtlich, welcher Algorithmus besser ist. Näherung: Betrachte nur sehr große Eingaben (meist sind alle Algorithmen schnell genug für kleine Eingaben). Dieses Vorgehen wird als Asymptotische Komplexität bezeichnet (N gegen unendlich).

Asymptotische Komplexität am Beispiel Polynom

Polynom: <math>a\,x^2+b\,x+c=p\!</math>

<math>x \!</math> sei die Eingabegröße, und wir betrachten die Entwicklung von <math>p \!</math> in Abhängigkeit von <math>x \!</math>.

• <math>x=0 \!</math>

  <math>p=c \!</math>

• <math>x=1 \!</math>

  <math>p=a+b+c \!</math>

• <math>x=1000 \!</math>

  <math>p=1000000a+1000b+c \approx 1000000a\!</math>

• <math>x \to \infty \!</math>

  <math>p \approx x^2a\!</math>

Für sehr große Eingaben verlieren also b und c immer mehr an Bedeutung, so dass am Ende nur noch a für die Komplexitätsbetrachtung wichtig ist.

O-Notation

• Intuitiv: Für große N dominieren die am schnellsten wachsenden Terme.
• Formale Definition:

  Asymptotische Komplexität

  Für zwei Funktionen f(x) und g(x) definiert man

  <math>f(x) \in \mathcal{O}(g(x))</math>

  (sprich "f ist in <math>\mathcal{O}(g)</math>" oder "f ist von derselben Größenordnung wie g") genau dann wenn es eine Konstante <math>c</math> und ein Argument <math>x_0</math> gibt, so dass

  <math>\forall x \ge x_0:\quad f(x) \le c g(x)</math>.

Die Idee hinter dieser Definition ist, dass g(x) eine wesentlich einfachere Funktion ist als f(x), die sich aber nach geeigneter Skalierung (Multiplikation mit c) und für große Argumente x im wesentlichen genauso wie f(x) verhält. Man kann deshalb in der Algorithmenanalyse f(x) durch g(x) ersetzen. <math>f(x) \in \mathcal{O}(g(x))</math> spielt für Funktionen eine ähnliche Rolle wie der Operator ≤ für Zahlen: Falls a ≤ b gilt, kann bei einer Abschätzung von oben ebenfalls a durch b ersetzt werden.

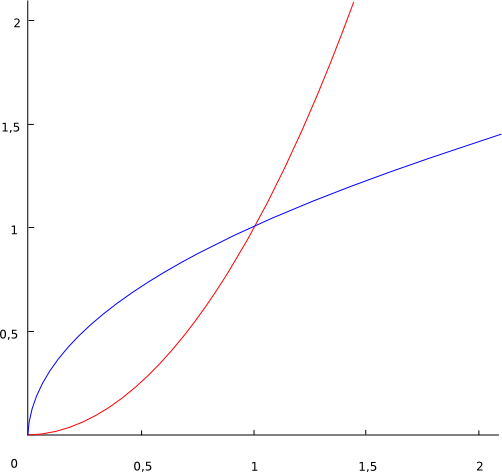
Ein einfaches Beispiel

Rot = <math>x^2 \!</math> Blau = <math>\sqrt{x} \!</math>

<math>\sqrt{x} \in \mathcal{O}(x^2)\!</math> weil <math>\sqrt{x} \le c\,x^2\!</math> für alle <math>x \ge x_0 = 1 \!</math> und <math>c = 1\!</math>, oder auch für <math>x \ge x_0 = 4 \!</math> und <math>c = 1/16</math> (die Wahl von c und x₀ in der Definition von O(.) ist beliebig, solange die Bedingungen erfüllt sind).

Komplexität bei kleinen Eingaben

Algorithmus 1: <math>\mathcal{O}(N^2) \!</math>
Algorithmus 2: <math>\mathcal{O}(N\log{N}) \!</math>

Algorithmus 2 ist schneller (von geringerer Komplexität) für große Eingaben, aber bei kleinen Eingaben (insbesondere, wenn der Algorithmus in einer Schleife immer wieder mit kleinen Eingaben aufgerufen wird) könnte Algorithmus 1 schneller sein, falls der in der <math>\mathcal{O}</math>-Notation verborgene konstante Faktor c bei Algorithmus 2 einen wesentlich größeren Wert hat als bei Algorithmus 1.

Eigenschaften der O-Notation (Rechenregeln)

1. Transitiv:

   <math>f(x) \in \mathcal{O}(g(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) \in \mathcal{O}(h(x)) \!</math>

2. Additiv:

   <math>f(x) \in \mathcal{O}(h(x)) \land g(x) \in \mathcal{O}(h(x)) \to f(x) + g(x) \in \mathcal{O}(h(x)) \!</math>

3. Für Monome gilt:

   <math>x^k \in \mathcal{O}(x^k)) \land x^k \in \mathcal{O}(x^{k+j}), \forall j \ge 0 \!</math>

4. Multiplikation mit einer Konstanten:

   <math>f(x) \in \mathcal{O}(g(x)) \to c\,f(x) \in \mathcal{O}(g(x))\!</math>

   andere Schreibweise:

   <math>f(x) = c\,g(x) \to f(x) \in \mathcal{O}(g(x))\!</math>

5. Folgerung aus 3. und 4. für Polynome:

   <math>a_0+a_1\,x + ... + a_n\,x^n \in \mathcal{O}(x^n)\!</math>

   Beispiel: <math>a\,x^2+b\,x+c \in \mathcal{O}(x^2)\!</math>

6. Logarithmus:

   <math>a, b \neq 1\!</math>

   <math>\log_{a}{x} \in \mathcal{O}(\log_{b}{x})\!</math>

   Die Basis des Logarithmus spielt also keine Rolle.

   Beweis hierfür:

   <math>\log_{a}{x} = \frac{\log_{b}{x}}{\log_{b}{a}}\!</math>

   Mit <math>c = 1 / \log_{b}{a}\,</math> gilt: <math>\log_{a}{x} = c\,\log_{b}{x}\!</math>.

   Wird hier die (zweite) Regel für Multiplikation mit einer Konstanten angewendet, fällt der konstante Faktor weg, also <math>\log_{a}{x} \in \mathcal{O}(\log_{b}{x})\!</math>.

   Insbesondere gilt auch <math>\log_{a}{x} \in \mathcal{O}(\log_{2}{x})\!</math>, es kann also immer der 2er Logarithmus verwendet werden.

O-Kalkül

Das O-Kalkül definiert wichtige Vereinfachungsregeln for Ausdrücke in O-Notation:

1. <math>f(x) \in \mathcal{O}(f(x))\!</math>
2. <math>\mathcal{O}(\mathcal{O}(f(x))) \in \mathcal{O}(f(x))\!</math>
3. <math>c\,\mathcal{O}(f(x)) \in \mathcal{O}(f(x))\,</math> für jede Konstante c
4. <math>\mathcal{O}(f(x))+c \in \mathcal{O}(f(x))\,</math> für jede Konstante c
5. Sequenzregel:

   Wenn zwei nacheinander ausgeführte Programmteile die Komplexität <math>\mathcal{O}(f(x))</math> bzw. <math>\mathcal{O}(g(x))</math> haben, gilt für beide gemeinsam:

   <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(f(x))</math> falls <math>g(x) \in \mathcal{O}(f(x))</math> bzw.

   <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(g(x))\!</math> falls <math>f(x) \in \mathcal{O}(g(x))</math>.

   Informell schreibt man auch: <math>\mathcal{O}(f(x)) + \mathcal{O}(g(x)) \in \mathcal{O}(max(f(x), g(x)))\!</math>

6. Schachtelungsregel bzw. Aufrufregel:

   Wenn in einer geschachtelten Schleife die äußere Schleife die Komplexität <math>\mathcal{O}(f(x))</math> hat, und die innere <math>\mathcal{O}(g(x))</math>, gilt für beide gemeinsam:

   <math>\mathcal{O}(f(x)) * \mathcal{O}(g(x)) \in \mathcal{O}(f(x) * g(x))\!</math>.

   Gleiches gilt wenn eine Funktion <math>\mathcal{O}(f(x))</math>-mal aufgerufen wird, und die Komplexität der Funktion selbst <math>\mathcal{O}(g(x))</math> ist.

O-Kalkül auf das Beispiel des Selectionsort angewandt

Selectionsort: Wir hatten gezeigt dass <math>f(N) = \frac{N^2}{2} - \frac{N}{2}</math>. Nach der Regel für Polynome vereinfacht sich dies zu <math>f(N) \in \mathcal{O}\left(\frac{N^2}{2}\right) \in \mathcal{O}(N^2)\!</math>.

Alternativ via Schachtelungsregel:

Die äußere Schleife wird (N-1)-mal durchlaufen: <math>N-1 \in \mathcal{O}(N)</math>

Die innere Schleife wird (N-i-1)-mal durchlaufen. Das sind im Mittel N/2 Durchläufe: <math>N/2 \in \mathcal{O}(N)</math>

Zusammen: <math>\mathcal{O}(N)*\mathcal{O}(N) \in \mathcal{O}(N^2)</math>

Nach beiden Vorgehensweisen kommen wir zur Schlussfolgerung, dass der Selectionsort die asymptotische Komplexität <math>\mathcal{O}(N^2)\!</math> besitzt.

Zusammenhang zwischen Komplexität und Laufzeit

Wenn eine Operation 1ms dauert, erreichen Algorithmen verschiedener Komplexität folgende Leistungen (wobei angenommen wird, dass der in der <math>\mathcal{O}</math>-Notation verborgene konstante Faktor immer etwa gleich 1 ist):

Komplexität	Operationen in 1s	Operationen in 1min	Operationen in 1h
<math>\mathcal{O}(N)</math>	1000	60.000	3.600.000
<math>\mathcal{O}(N\log_2{N})</math>	140	4895	204094
<math>\mathcal{O}(N^2)</math>	32	245	1898
<math>\mathcal{O}(N^3)</math>	10	39	153
<math>\mathcal{O}(2^N)</math>	10	16	21

Exponentielle Komplexität

Der letzte Fall <math>\mathcal{O}(2^N)</math> ist von exponentieller Komplexität. Das bedeutet, dass eine Verdopplung des Aufwands nur bewirkt, dass die maximale Problemgröße um eine Konstante wächst. Algorithmen mit exponentieller (oder noch höherer) Komplexität werden deshalb als ineffizient bezeichnet. Algorithmen mit höchstens polynomieller Komplexität gelten hingegen als effizient.

In der Praxis sind allerdings auch polynomielle Algorithmen mit hohem Exponenten meist zu langsam. Als Faustregel kann man eine praktische Grenze von <math>\mathcal{O}(N^3)</math> ansehen. Bei einer Komplexität von <math>\mathcal{O}(N^3)</math> bewirkt ein verdoppelter Aufwand immer noch eine Steigerung der maximalen Problemgröße um den Faktor <math>\sqrt[3]{2}</math> (also eine multiplikative Vergrößerung um ca. 25%, statt nur einer additiven Vergrößerung wie bei exponentieller Komplexität).

(Vorlesung 8.5.)

(noch in Arbeit!!!)

Beispiel: running Average

Annahme: Array-Zugriff hat eine Komplexität von O(1)

Schritte	Version 1 O(N * k)	Komplexität	Version 2 O(N)	Komplexität
1.	r = [0] * len(a)	O(1)	if k > len(a):	O(1)
2.	if k > len(a):	O(1)	raise RuntimeError ("k zu groß")
3.	raise RuntimeError ("k zu groß")		r = [0] * len(a)	O(1)
4.	for j in range(k, len(a)):	O(N-k) = O(N)	for i in range(k):	O(k)
5.	for i in range(j-k+1, j+1):	O(k)	r[k] += a[i]	O(1)
6.	r[j] += a[i]	O(1)	for j in range(k+1, len(a)):	O(N-k) = O(N)
7.	r[j] /= float(k)	O(1)	r[j] += (a[j] - a[j-k] + r[j-1])	O(1)
8.	return r	O(1)	for j in range(len(a)):	O(N)
9.			r[j /= float(k)]	O(1)
10.			return r	O(1)

Trotz, dass Version 2 mehr Schritte benötigt besitzt das Programm eine geringere Komplexität.

Berechnung der Komplexität

Berechnung der Komplexität von Version 1

(Wiederholung der Rechenregeln:siehe Vorlesung 7.5.)

Zuweisungen
äußere Schleife = f(x)
innere Schleife = g(x)

4. Schritt: for j in range(k, len(a)) = äußere Schleife

f(x) = O(N)(siehe Tabelle)

5. Schritt: for i in range(j-k+1, j+1) = innere Schleife

g(x) = O(k)

Multiplikationsregel ohne Konstante:
O(f(x) * O(g(x)) ∈ O(f(x) * g(x))

Multiplikationsregel angewendet auf Version 1
O(N) * O(k) ∈ O(N * k)
Komplexität von Version 1 = O(N * k)

Berechnung der Komplexität von Version2

siehe Tabelle

Zuweisungen

6.Schritt: for j in ange(k+1, len(a)):

f₁(x) = O(N)

8.Schritt: for j in range(len(a)):

f₂(x) = O(N)

4.Schritt: for i in range(k):

g(x) = O(k)

Additionsregel:
O(f(x) + g(x)) = O(f(x))
falls g(x) ∈ O(f(x)) [O(max(f(x),g(x))]
O(f(x) + g(x)) ∈ O(g(x))
falls f(x) ∈ O(g(x)) [O(max(f(x),g(x))]

Anwendung der Additionsregel auf Version 2
O(f₁(x)) + O(f₂(x)) + O(g(x))
O(N) + O(N) +O(k) = O(N), falls O(k) ∈ O(N) [O(max(O(N),O(k]
(da wir wissen O(k) < O(N):
if k > len(a):

raise RuntimeError("k zu groß")

Daraus folgt:
→ k < len(a) → for-Schleifen die über k iterieren haben eine kleinere Komplexität als for-Schleifen die über len(a) iterieren)

Komplexität von Version 2 = O(N)

Fazit

Obwohl Version 2 mehr Schritte benötigt hat sie eine geringere Komplexität, da die for-Schleifen nicht wie bei Version 1 verschachtelt/untergeordnet sind. Bei verschachtelten for-Schleifen muss die Multiplikationsregel angewendet → höhere Komplexität

Die gerade berechnete Komplexität gilt nur unter der Annahme, dass Array-Zugriffe eine Komplexität von O(1) besitzen

Allgemein: Algorithmen-Analysen beruhen auf der Annahme, dass Zugriff auf die Daten optimal schnell sind, dass heißt dass die geeigneteste Datenstruktur verwendetet wird. → Ansonsten: Komplexitätsverschlechterung!

Beispiel für eine Verschlechterung der Komplexität durch Verwendung einer anderen Datenstruktur als die Optimalste

Beispiel: Verwende eine verkettete Liste anstatt einem Array

Verkettete Liste	Komplexität
L[j]
r = L.head	O(1)
while j > 0:
r = r.next	O(1)
j -= 1	O(1)
gefunden: r.data	O(1)

<math> \Bigg\rbrace </math> O(j)
r[j] = r[j] + a[i] → O(1) → O(N), falls a[i]= O[N]

Fazit:

Der Arrayzugriff einer verketteten Liste hat eine Komplexität von O(N).
Würden wir in unserem running Average-Beispiel(siehe oben) auf eine verkettete Liste zugreifen hätten wir anstatt O(1) eine Komplexität von O(N) für den Zugriff auf unser Array.

Beispiel: running-Average mit verketteter Liste

Schritte	Version 1 O(N * k)	Komplexität
1.	verkettete Liste(siehe oben)	O(N)
2.	if k > len(a):	O(1)
3.	raise RuntimeError ("k zu groß")
4.	for j in range(k, len(a)):	O(N-k) = O(N)
5.	for i in range(j-k+1, j+1):	O(k)
6.	r[j] += a[i]	O(1)
7.	r[j] /= float(k)	O(1)
8.	return r	O(1)

Zuweisungen
äußere Schleife = f₂(x)
innere Schleife = g(x)

verkettete Liste

f₁(x) = O(N)

4. Schritt: for j in range(k, len(a)) = äußere Schleife

f₂(x) = O(N)(siehe Tabelle)

5. Schritt: for i in range(j-k+1, j+1) = innere Schleife

g(x) = O(k)

Multiplikationsregel ohne Konstante:
O(f(x) * O(g(x)) ∈ O(f(x) * g(x))

Multiplikationsregel angewendet auf Version 1 mit einer verketteten Liste

O(N) * O(N) * O(k) ∈ O(N² * k)

Die Komplexität von Version 1 mit einer verketteten Liste wäre O(N² * k)

→ Die richtige Datenstruktur ist wichtig, da es sonst zu einer Komplexitätsverschlechterung kommen kann!

Auf Version 2 unseres runningAverage-Beispiels hätte eine verkettete Liste allerdings keine Auswirkungen, da die Additionsregel bei der Komplexitätsberechnung angewendet würde und somit Version 2 immer noch eine Komplexität von O(N) hätte.

Amortisierte Komplexität

Bis jetzt wurde die Komplexität nur im schlechtesten Fall(Worst Case) betrachtet, die Komplexität im schlechtesten Fall schwankt jedoch.
Die amortisierte Komplexität beschäftigt sich mit der Komplexität im durschnittlichen/typischen Fall(Average Case)

Zum weiter Lesen: [Wikipedia: Amortisierte Laufzeitanalyse]

Beispiel: Inkrementieren von Binärzahlen

Frage: Was kostet eine Operation im Durchschnitt?

Annahme: Bei jeder Operation wird ein Gehalt vom Wert 1 bezahlt, dass dem Guthaben zugeschrieben wird, wenn die Kosten das Gehalt decken.

Kosten <= Gehalt → es wird gespart

Kosten > Gehalt → Guthaben - Gehalt werden für die Kosten verbraucht

Schritte	Zahlen	Kosten	Kosten + Sparen	Guthaben
1.	00001	1	2	1
2.	00010	2	2	1
3.	00011	1	2	2
4.	00100	3	2	1

Die Kosten ergeben sich aus der Anzahl der Ziffern die von 1 nach 0, bzw. von 0 nach 1 verändert werden

Rechnung:

1. Schritt: Kosten: 1 <= Gehalt: 1

→ es wird gespart

2. Schritt: Kosten: 2 > Gehalt: 1

→ es wird nicht gespart

→ Guthaben bleibt so wie es ist

3. Schritt: Kosten: 1 <= Gehalt: 1

→ es wird gespart

4. Schritt: Kosten: 3 > Gehalt: 1

→ Guthaben: 2 - Gehalt: 1 = 1

→ es wird eine 1 vom Guthaben genommen um die Kosten zu zahlen

Zum weiter Lesen: [Wikipedia Account-Methode]

Fazit

Die amortisierte Komplexität beschäftigt sich mit dem Durchschnitt aller Operation im ungünstigsten Fall. Operationen mit hohen Kosten fallen bei der amortisierten Komplexität nicht so ins Gewicht und Algorithmen, die eine "teure" Operation besitzen, ansonsten jedoch aus "billigen" Operationen bestehen, haben eine niedrigere Komplexität.

In unserem Beispiel fällt der 4. Schritt bei den Kosten schlußendlich nicht so ins Gewicht, da wir die Kosten aus unserem Guthaben mitbezahlen können → tatsächliche Kosten = 3, Kosten + Sparen = 2

→ Der Algorithmus besitzt durch dieses Verfahren eine niedrigere Komplexität

statisches Array

Ein statisches Array hat eine feste Größe N und besitzt eine Komplexität von O(N).
Wird das Array um ein Element erweitert, muss ein neues Array mit der Größe N+1 erzeugt werden.

Anhängen eines weiteren Elements an ein statisches Array:

altesArray = [0,1,2,3]
altesArray.append('x')

1. Es wird ein neues Array der Größe N+1 erzeugt → neuesArray = [_,_,_,_,_] Komplexität: O(N+1) = O(N)
2. Die Daten aus dem alten Array werden in das neue Array mit der Länge N+1 kopiert → neuesArray = [0,1,2,3,_] Komplexität: O(N) (Die Operation besitzt nur eine Komplexität von O(N), wenn das Kopieren eines Elements eine Komplexität von O(1) besitzt)
3. 'x' wird an die letzte Stelle des neuen Arrays geschrieben → neuesArray = [0,1,2,3,'x'] Komplexität: O(1)

Additionsregel:
O(N) + O(N) + O(1) ∈ O(N), falls O(1) ∈ O(N) [O(max(O(N),O(1))] (Bedingung: N > 1)

dynamisches Array

Beim dynamischen Array werden mehr Speicherelemente reserviert als zur Zeit benötigt. Es gibt verschiedene Möglichkeiten wie ein dynamisches Array realisiert werden kann.

capacity = Anzahl der möglichen Elemente, die in das Array passen size = Anzahl der Elemente, die im Array gespeichert sind data = statisches Array der Größe "capacity" A

Beispiele für mögliche Vorgehensweisen eines dynamischen Arrays beim Zufügen eines neuen Elements: (size == capacity)

• Ein neues statisches Array der Größe size == capacity wird erzeugt
• capacity wird verdoppelt
  

→ neue capacity = 2 * alte capacity

• capacity wird um einen Prozentsatz vergrößert
  

&rarr neue capacity = alte capacity * c, c > 1

• ...

Folge: Das Hinzufügen eines neuen Elements in ein dynamisches Array ist amortisiert, die Operation besitzt eine Komplexität von O(1).

Analyse des dynamischen Arrays

Durchschnitt der Gesamtkosten für N-maliges append = <math>\frac{1}{N} \sum_{i = 1}^N Kosten(i)</math>
N-maliges append sind amortisierte Kosten, da size < capacity

Φ(t) = 2 * size - capacity

altesArray = [0,1,2,None]

altesArray.append('x') Φ(t) = 2 * 3 - 4 = 2

neuesArray = [0,1,2,'x',None,None]

Fall 1: size < capacity

→ amortisierte Kosten, da kein Umkopieren nötig ist

Potential vor append: Φ(i-1) = 2(i-1) - capacity
Potential nach i-tem append: Φ (i) = 2(i) - capacity

size	capacity	Kosten 1.append	Summe Kosten	Durchschnittskosten	Φi = 2 * size - capacity (i = size)	Potenzialdifferenz Δ Φi = Φi - Φi-1	amortisierte Kosteni = Kosteni + Δ Φi